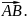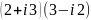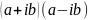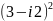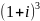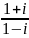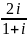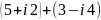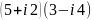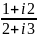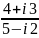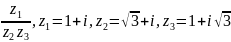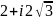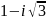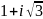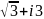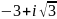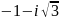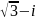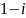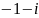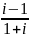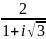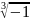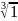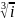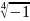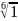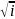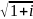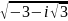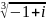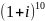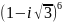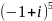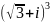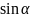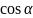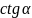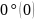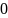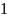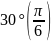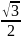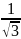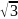- •Глава 1
- •§ 1. Основные понятия
- •§ 2. Грани числовых множеств
- •§ 3. Абсолютная величина вещественного числа
- •Глава 2
- •§1. Числовые последовательности
- •1. Определение числовой последовательности.
- •3. Бесконечно большие и бесконечно малые последовательности.
- •§2. Сходящиеся последовательности
- •Определение предела последовательности.
- •2. Основные свойства сходящихся последовательностей
- •§3. Монотонные последовательности
- •Определение монотонных последовательностей.
- •Признак сходимости монотонных последовательностей.
- •3. Число
- •Глава 3.
- •§ 1.Направленные отрезки и их величины. Числовая прямая
- •§ 2. Прямоугольная (декартова) система координат
- •§ 3. Простейшие задачи аналитической геометрии на плоскости
- •§ 4. Полярные координаты
- •§ 5. Уравнение линии как множество точек плоскости
- •§ 6. Линии первого порядка
- •Уравнение прямом с угловым коэффициентом
- •Уравнение прямой, проходящей через данную точку m( , ) с данным угловым коэффициентом:
- •Уравнение прямой, проходящей через две данные точки м1( ; ) и м2( ; ):
- •Общее уравнение прямой
- •98. Найти расстояния точек а (4; ?
- •§ 7. Смешанные задачи на прямую
- •§ 8. Линии второго порядка
- •Глава 4
- •§ 1.Основные понятия
- •§ 2. Предел и непрерывность функции
- •Свойства пределов.
- •§3. Сравнение бесконечно малых
- •Глава 5
- •§ 1. Понятие производной
- •§2. Вычисление производных
- •§3. Понятие дифференциала
- •§4. Производные и дифференциалы высших порядков
- •Глава 6
- •§ 1. Первообразная и неопределенный интеграл
- •2. Основные свойства неопределенного интеграла.
- •3. Таблица основных интегралов.
- •§2. Основные методы интегрирования
- •§4 Определённый интеграл.
- •2.Основные свойства определенного интеграла.
- •Глава 7.
- •§ 1. Определители
- •3. Свойства определителей.
- •§ 2. Исследование системы трех уравнений первой степени с тремя неизвестными
- •Глава 8
§ 2. Исследование системы трех уравнений первой степени с тремя неизвестными
Рассмотрим систему трех уравнений первой степени с тремя неизвестными x, y, z:
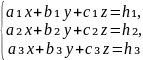 (1)
(1)
(Коэффициенты , , , b₁, b₂, b₃, c₁, c₂, c₃ и свободные члены h₁, h₂, h₃ считаются заданными).
Тройка чисел x₀, y₀, z₀ называется решением системы (1), если в результате подстановки этих чисел вместо x, y, z все три уравнения (1) обращаются в тождество.
В дальнейшем основную роль будут играть следующие четыре определителя:
Δ
=
,
Δx
=
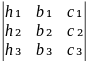 , Δy
=
, Δy
=
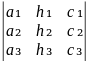 ,
,
Δz
=
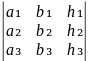 .
.
Определитель Δ называется определителем системы (1). Определители Δx, Δy, Δz получаются из определителя системы Δ заменой свободными членами элементов соответственно первого, второго и третьего столбцов.
Если определитель Δ системы (1) отличен от нуля (Δ ≠ 0), то существует, и притом единственное, решение этой системы, и оно выражается формулами:
x
=
 , y
=
, y
=
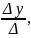 z
=
z
=
 . (2)
. (2)
Пример 1. Найти решения системы:
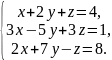
Решение. Составляем определитель системы:
Δ
=
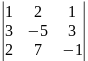 = 33.
= 33.
Так как Δ ≠ 0, то данная система имеет единственное решение, определяемое формулами (2). Имеем:
Δx
=
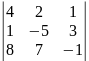 = 33, Δy
=
= 33, Δy
=
 = 33, Δz
=
= 33, Δz
=
 = 33.
= 33.
По формулам (2) находим:
x
=
– 1, y
=
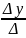 – 1, z
=
– 1.
– 1, z
=
– 1.
Следовательно, x – 1, y – 1, z – 1 – решение данной системы.
Если определитель Δ системы (1) равен нулю (Δ = 0) и хотя бы один из определителей Δx, Δy, Δz отличен от нуля, то система не имеет решения (несовместна).
Пример 2. Найти решение системы:

Решение.
Так как Δ =
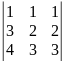 = 0, а Δy
=
= 0, а Δy
=
 = 1 ≠ 0, то данная система не имеет решения.
= 1 ≠ 0, то данная система не имеет решения.
Наконец, если Δ = 0 и Δx= Δy= Δz=0, то система (1) либо совсем не имеет значений, либо если система (1) имеет хотя бы одно решение, то она имеет бесконечно много решений.
В задачах 38-45 установить, что системы имеют единственное решение и найти его.
38.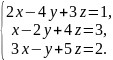 39.
39.

40.
 41.
41.
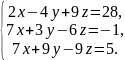
42.
 43.
43.
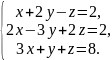
44. 45.
45.
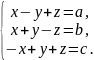
46. Найти решения системы. 47. Найти решение системы.

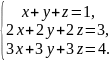
48. Найти решение системы.

49. Найти решение системы.

50. Определить, при каких значениях и система
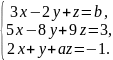
имеет единственное решение;
не имеет решений;
имеет бесконечно много решений.
Глава 8
Комплексные числа
Введение комплексных чисел вызвано тем, что во множестве вещественных чисел не выполнено извлечение корня четной степени из отрицательного числа.
Определение. Комплексным числом z называется упорядоченная пара вещественных чисел (x; y), т.е. z = (x; y). При этом x называется вещественной, а y – мнимой частью комплексного числа.
Комплексное число z = (x; y) изображается на плоскости Оxy точкой с координатами (x; y). Плоскость Оxy в этом случае называется условно комплексной плоскостью.
Комплексное
число (x; y) при
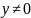 называется мнимым.
Мнимое
число (0; y) называется чисто
мнимым,
а чисто мнимое число (0;1) – мнимой
единицей и
обозночается буквой i,
т.е.
i
=
(0;1). По определению полагают (x;0) = x, (0;y)
= iy,
(0;0) = 0.
называется мнимым.
Мнимое
число (0; y) называется чисто
мнимым,
а чисто мнимое число (0;1) – мнимой
единицей и
обозночается буквой i,
т.е.
i
=
(0;1). По определению полагают (x;0) = x, (0;y)
= iy,
(0;0) = 0.
Действия над комплексными числами. Пусть z₁ = (x₁;y₁) и z₂ = (x₂;y₂) – два комплексных числа. Тогда суммой комплексных чисел z₁ и z₂ называется комплексное число
 ;
;
разностью – комплексное число
 -
-
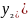 ;
;
произведением – комплексное число

частным – комплексное число
 ,
,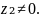
Пример 1. Доказать, что i² = -1.
Решение.
В силу определения произведения
комплексных чисел имеем
 ,
что и требовалось доказать.
,
что и требовалось доказать.
Алгебраическая
форма комплексного числа. Любое
комплексное число z = (x; y) можно представить
в виде
 и производить над комплексными числами
действия по обычным правилам алгебры
многочленов. Запись
и производить над комплексными числами
действия по обычным правилам алгебры
многочленов. Запись
 называется алгебраической
формой комплексного числа.
называется алгебраической
формой комплексного числа.
Пример
2.
Найти сумму чисел
 и
и
 .
.
Решение. Имеем
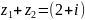 +
(
+
(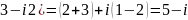
Пример
3.
Разделить число
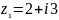 на число
на число
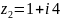 .
.
Решение. Практически деление комплексных чисел выполняется по следующему правилу:
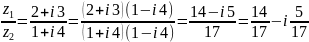
Комплексное
число
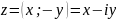 называется комплексно-сопряженным
числу
называется комплексно-сопряженным
числу
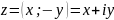 и изображается на комплексной плоскости
точкой, симметричной точке z относительно
оси Оx.
и изображается на комплексной плоскости
точкой, симметричной точке z относительно
оси Оx.
Пример
4.
Решить уравнение
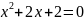 .
.
Решение.
Применив к данному уравнению известное
правило нахождения корней уравнения,
получим
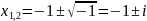 .
.
Данное
уравнение вещественных корней не имеет;
его корни комплексно-сопряженные, т.е.
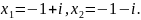
Тригонометрическая форма комплексного числа. Комплексное число
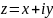 определяется
упорядоченной парой вещественных чисел
(x; y). По формулам
определяется
упорядоченной парой вещественных чисел
(x; y). По формулам
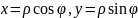 ,
связывающим полярные и прямоугольные
координаты, получим тригонометрическую
форму записи комплексного числа
:
,
связывающим полярные и прямоугольные
координаты, получим тригонометрическую
форму записи комплексного числа
:
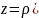 .
.
Число
называется модулем,
а
число
- аргументом
комплексного
числа
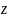 .
Они обозначаются так:
.
Они обозначаются так:
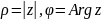 ,
причем аргумент
определен с точностью до слагаемого
,
причем аргумент
определен с точностью до слагаемого
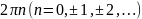 ,
модуль имеет значение
,
модуль имеет значение
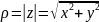 .
.
Пример
5.
Представить в тригонометрической форме
число
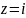 .
.
Решение.
Для
имеем:
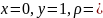
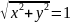 ,
,
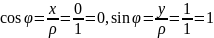 .
Этим значениям косинуса и синуса
соответствует значение аргумента
.
Этим значениям косинуса и синуса
соответствует значение аргумента
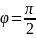 .
Следовательно,
.
Следовательно,
 .
.
Пусть
 и
и
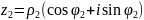 .
Тогда умножение и деление комплексных
чисел
.
Тогда умножение и деление комплексных
чисел
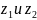 определяются по формулам
определяются по формулам
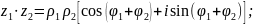
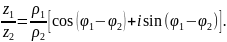
Пусть
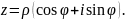 Тогда возведение в степень и извлечение
корня n-й степени (n – целое положительное
число) осуществляется по формулам
Тогда возведение в степень и извлечение
корня n-й степени (n – целое положительное
число) осуществляется по формулам
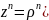
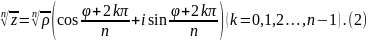
В
частности, если в формуле (1) положить
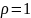 ,
то получим формулу
,
то получим формулу
 которая называется формулой
Муавра.
которая называется формулой
Муавра.
Выполнить действия:
|
|
|
Решить уравнения: 1)
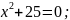
2)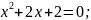
3)
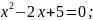
4)
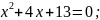
5)
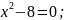
6)
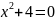
и проверить подстановкой корней в уравнение.
Представить в тригонометрической форме комплексные числа:
|
|
|
Найти все значения корней:
|
|
|
|
Вычислить по формуле Муавра:
|
|
|
|
Справочный материал
Тригонометрия
Тригонометрические функции суммы и разности углов
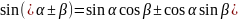 ,
,
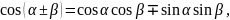
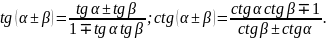 Тригонометрические
функции двойных, тройных и половинных
углов
Тригонометрические
функции двойных, тройных и половинных
углов
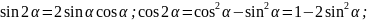
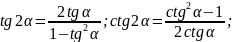
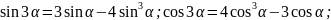
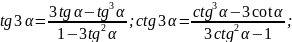
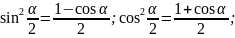
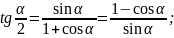
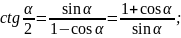
Формулы универсальной тригонометрической подстановки
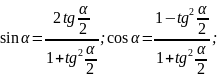

Преобразование суммы тригонометрических функций в произведение
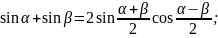
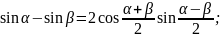
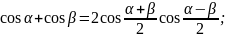
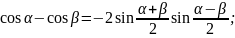
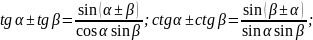
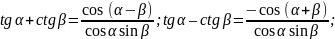
Преобразование произведения тригонометрических функций в сумму
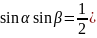
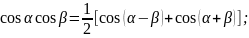

Решение
тригонометрических уравнений

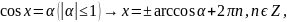
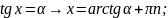
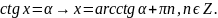
Частные случаи
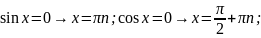
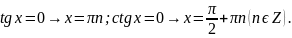
Численные значения тригонометрических функций
Аргумент |
Функция |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соотношения между элементами треугольника
Обозначения:
a,b,c
– стороны треугольника ABC,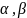 ,
,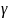 -углы
треугольника, лежащие против сторон
а,b
,c
соответственно, R-радиус
описанной окружности,
-углы
треугольника, лежащие против сторон
а,b
,c
соответственно, R-радиус
описанной окружности,
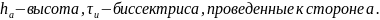
Теорема косинусов
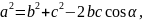
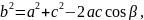
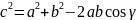 .
Формулы
сокращенного умножения:
.
Формулы
сокращенного умножения:
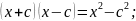
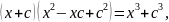
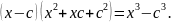 Формула
Виета для корней приведенного квадратного
уравнения
Формула
Виета для корней приведенного квадратного
уравнения
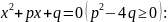

 Корни
квадратного уравнения
Корни
квадратного уравнения
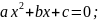
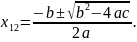 Корни
квадратного уравнения с четным вторым
коэффициентом
Корни
квадратного уравнения с четным вторым
коэффициентом
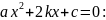
 Корни
приведенного квадратного уравнения
Корни
приведенного квадратного уравнения
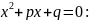
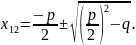 Степени:
Степени:

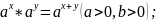

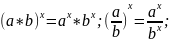 Определение
квадратного корня
Определение
квадратного корня
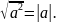
Логарифмы

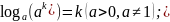
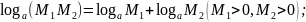
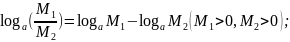
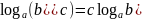
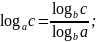
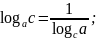
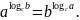 Десятичные
логарифмы – логарифмы
по основанию 10 числа a
– обозначают l
Десятичные
логарифмы – логарифмы
по основанию 10 числа a
– обозначают l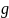 a.
a.
Натуральные
логарифмы – логарифмы
по основанию e=2.71828182…
-
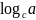 обозначают ln
a.
обозначают ln
a.
Свойства линий в треугольнике
Свойства медиан: пересекаются в одной точке; в очке пересечения делятся в отношении 2:1, считая от вершины; каждая медиана делит треугольник на два равновеликих треугольника.
Свойства средней линии: равна половине параллельной ей стороны; отсекает треугольник с площадью, равной одной четвертой площади треугольника.
Свойства
биссектрис: пересекаются
в одной точке: если
 - отрезки, на которые делит сторону a
основание биссектрисы
- отрезки, на которые делит сторону a
основание биссектрисы
 =b:c,
где b
и с – стороны, прилежащие к отрезкам
соответственно.
=b:c,
где b
и с – стороны, прилежащие к отрезкам
соответственно.
Свойство высот: пересекаются в одной точке;

1 Напомним, что координатной прямой называется прямая, на которой выбраны точка, являющаяся началом отсчета, масштабный отрезок и положительное направление.
2
Иногда обозначают