Глава 1

ВЕЩЕСТВЕННЫЕ (ДЕЙСТВИТЕЛЬНЫЕ) ЧИСЛА

§ 1. Основные понятия

1. Представление вещественных чисел в виде бесконечных десятичных дробей. Множество вещественных чисел разбивается на два множества: рациональных и иррациональных чисел. Рациональным называется число, которое можно представить в виде 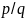, где и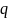 — целые числа, причем 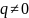. Иррациональным называется всякое вещественное число, которое не является рациональным.

Любое вещественное число представимо в виде бесконечной десятичной дроби, где 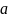– любое целое число, а 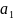, , 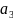… 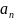– числа, принимающие целые значения от 0 до 9 (0≤ ≤9).

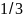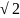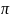Всякое рациональное число p/q является либо целым, либо его можно представить в виде конечной или периодической бесконечной десятичной дроби. Иррациональное же число представляется непериодической бесконечной десятичной дробью. Например, рациональные числа и представляются соответственно следующими десятичными дробями: 0,75 и 0,333 ...; иррациональные числа и представляются соответственно непериодическими бесконечными десятичными дробями: 1,41421356... и 3,14159....

1. Определить, какие из данных бесконечных десятичных дробей рациональные числа, какие – иррациональные: 5.424242...; 0,32375375...; 1,313013001...; 7,1308367... .

2. Доказать, что число

0,1010010001 ... 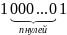... иррационально.

3. Привести пример, показывающий, что сумма двух иррациональных чисел может быть числом рациональным.

4. Привести пример, показывающий, что разность двух иррациональных чисел может быть числом рациональным.

5. Доказать, что сумма, разность, произведение и частное рационального числа 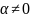и иррационального числа есть число иррациональное.

6. Доказать, что — иррациональное число.

7. Доказать, что не является рациональным числом.

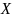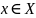2. Некоторые числовые множества. Пусть — некоторое множество вещественных чисел. Тогда запись означает, что число принадлежит 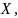а запись 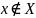означает, что число не принадлежит .

Если 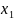... — некоторые числа, то запись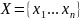 означает, что множество состоит из чисел ... . Аналогичный смысл имеет запись запись .

Пусть и 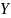— два множества. Запись 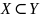означает, что есть подмножество множества .

Пусть 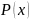– какое-то свойство числа . Тогда запись 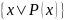обозначает множество всех таких чисел, которые обладают свойством .

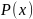Пусть и 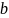– два числа, причем 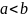, Будем использовать следующие обозначения и терминологию:

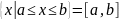─ отрезок (сегмент);

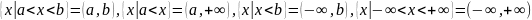– интервалы;

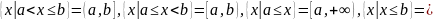– полуинтервалы.

Все эти множества называются промежутками. Промежутк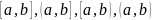и называются конечными; и – их концами. Остальные промежутки называются бесконечными.

Вещественные числа изображаются точками на координатной прямой¹, поэтому множество всех вещественных ( , 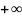) называют числовой прямой, а сами числа – точками.

Пусть – произвольная точка числовой прямой и 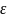(греческая буква «эпсилон») – положительное число. Тогда (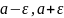 ) называется 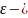окрестностью точки .

8. Чем отличается интервал 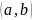от отрезка ?

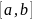9. Из отрезка удален интервал Что осталось?

10. Из отрезка удален интервал Какие промежутки остались?

11. Из интервала 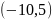удален отрезок 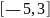. Какие промежутки остались?