1. Дифференциальные передачи

Дифференциальной передачей или дифференциалом называется планетарный механизм, у которого центральные колёса вращаются. Дифференциалы применяются для сложения движений двух ведущих звеньев на ведомом звене или для разложения движения ведущего звена на два независимых движения ведомых звеньев.

Схемы простейших дифференциальных передач представлены на рис. 8.

Рис. 8. Простейшие дифференциальные передачи

Центральные колёса 1 и 3 вращаются вокруг расположенных на одной прямой осей с угловыми скоростями ₁ и ₃. Водило H с _H вращается вокруг общей геометрической оси колеса 1 и 3. Сателлиты 2-2` установлены в подшипнике водила H и совершают сложное движение: вокруг собственной оси и вместе с H вокруг оси III на рис. 8, а и вокруг оси I на рис. 8, б (переносное движение).

Степень подвижности рассматриваемых механизмов:

.

Т.е. дифференциал должен иметь два ведущих звена, например, звенья 1 и H. Тогда угловые скорости звеньев 2 и 3 будут вполне определёнными.

В основе определения передаточных отношений дифференциальной передачи положен метод обращенного движения. Для этого всем звеньям механизма сообщается дополнительное вращение с угловой скоростью (-_H) . В результате водило становится неподвижным и получается рядовая передача, для которой можно определить передаточные отношения по формулам (2) и (3).

Например, для схемы рис. 8, а получаем таблицу:

№ звена	Первоначальная угловая скорость звена	Угловая скорость звена в обращенном движении
1	1	1 - H
2	2	2 - H
2`	2`	2` - H
3	3	3 - H

Следовательно, для обращенного механизма

(4),

где - передаточное отношение обращенного механизма при неподвижном водиле H.

В общем случае для n колёс получаем формулу Виллиса:

(5)

Формула Виллиса используется при определении угловых скоростей сателлитов. Для этого рассматривается зацепление сателлита с центральным колесом, угловая скорость которого известна. Например, для рис. 8, а

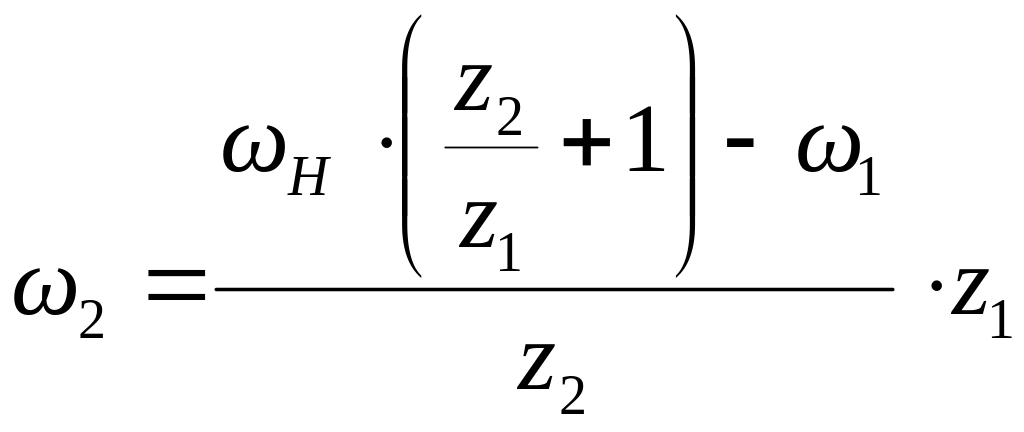
Пример расчёта дифференциальной передачи.

Пусть дана дифференциальная передача, у которой известны числа зубцов всех колёс (рис. 9):

Рис. 9. Дифференциальная передача. Пример расчета.

z₁ =80; z₂ =20; z_2' =30; z₃ =30; n₁=300 об/мин; n_H=200 об/мин.

Требуется определить числа оборотов всех колёс передачи.

По формуле Виллиса:

об/мин.

Знак «–» перед значением n₃ соответствует случаю, когда направление вращения звена 4 противоположно направлению вращений звеньев 1 и H.

Далее определяем число оборотов звена 2:

об/мин,

n₂= n_2’, так как z₂ и z_2’ жестко скреплены на одном валу.

Если в дифференциальной передаче ведущие звенья связать между собой дополнительной зубчатой передачей, то получится замкнутая дифференциальная передача.

2. Дифференциальная замкнутая передача

Замкнутая дифференциальная передача имеет одно ведущее звено (подвижность ) и подвижные центральные колёса.

В качестве примера рассмотрим дифференциальную передачу, (рис. 10, а) в которой два ведущих звена 1 и H. Если эти звенья замкнуть рядом колёс 1`, 5`, 5, 4, то получится замкнутая дифференциальная передача (рис. 10, б).

Рис. 10 Получение дифференциальной замкнутой передачи

Обычно для кинематического исследования таких передач составляется система двух алгебраических уравнений. Одно из них – уравнение для определения передаточного отношения от ведущего звена к ведомому звену дифференциальной части с помощью формулы Виллиса. Второе уравнение – уравнение замкнутости для определения передаточного отношения рядовой части передачи.

В результате решения полученной системы определяются угловые скорости всех звеньев, и соответственно, передаточное отношение механизма.

Для случая на рис. 10, б принимаем за ведущее звено 1. Система уравнений записывается в виде:

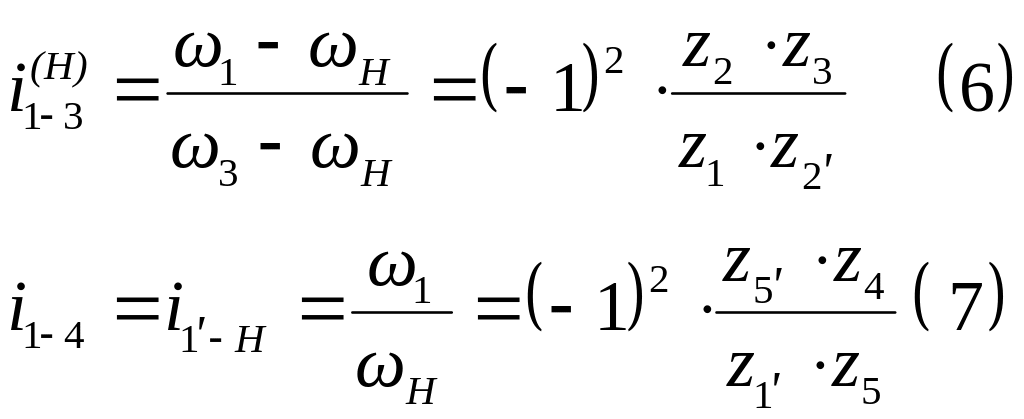
Числитель и знаменатель левой части уравнения (6) делим на ₁:

,

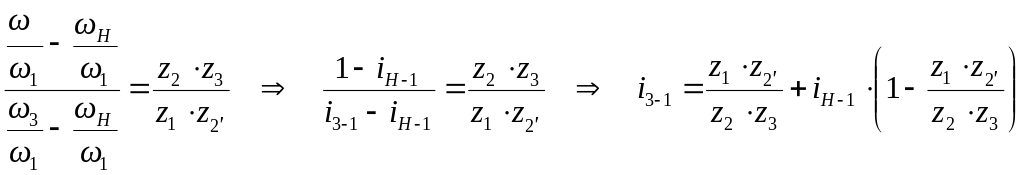используя (7), получаем

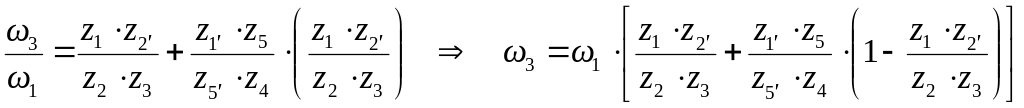
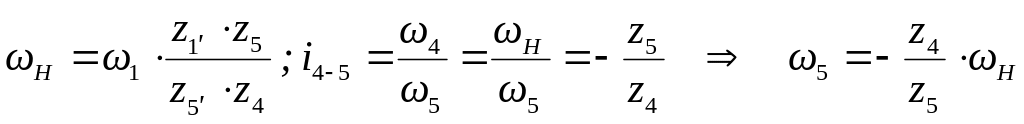
Для определения угловых скоростей сателлитов используем методику из предыдущего примера:

.