Линейная диаграмма

Рис. 5. Динамика ввода в действие зданий за 2007-2011гг. в Волгоградской области⁴

Общий вид графика зависит от правильного соотношения масштабов на осях абсцисс и ординат. В противном случае колебания будут либо малозаметными, либо слишком резкими. Если данные относятся к различным периодам времени, интервалы между ними при нанесении на оси абсцисс должны быть пропорциональны длительности периодов. При помощи линейных диаграмм можно выражать одновременно ряд пока­зателей, что даёт возможность сравнивать их друг с другом.

Графическое изображение рядов распределения

Анализ рядов распределения наглядно можно проводить на основе их графического изображения. Для этой цели строят полигон, гистограмму, огиву и кумуляту распределения.

Полигон используется при изображении дискретных вариационных рядов. Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат наносится шкала для выражения величины частот. Полученные на пересечении оси абсцисс (х) и оси ординат (у) точки соединяются прямыми линиями, в результате чего получают ломаную линию, называемую полигоном частот. Иногда для замыкания полигона предлагается крайние точки (слева и справа на ломаной линии) соединить с точками на оси абсцисс, в результате чего получается многоугольник.

Например, изобразим графически распределение жилого фонда по типу квартир, представленных в табл. 1.

Таблица 1.

Распределение жилого фонда городского района по типу квартир

(цифры условные)

№ п/п	Группы квартир по числу комнат	Число квартир, тыс. ед.
1 2 3 4 5	1 2 3 4 5	10 35 30 15 5
	Всего:	95

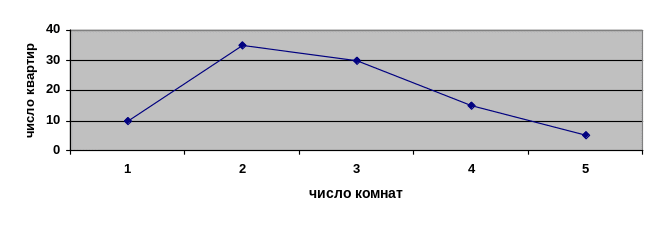
Рис. 6. Полигон распределения жилого фонда

Гистограмма применяется для изображения интервального вариационного ряда.

При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенным на соответствующих интервалах.

Высота столбиков должна быть пропорциональна частотам. В результате получается график, на котором ряд распределения изображен в виде смежных друг с другом столбиков.

Гистограмма может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединить прямыми линиями.

При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах. Это необходимо сделать для устранения влияния величины интервала на распределение интервала и получения возможности сравнивать частоты.

Плотность распределения – это частота, рассчитанная на единицу ширины интервала, то есть, сколько единиц в каждой группе приходится на единицу величины интервала.

Изобразим графически интервальный ряд распределения, приведенный в табл. 2.

Таблица 2.

Распределение семей по размеру жилой площади, приходящейся на одного человека (цифры условные)

№ п/п	Группы семей по размеру жилой площади, приходящейся на одного человека, м3	Число семей с данным размером жилой площади	Накопленное число семей
1 2 3 4 5	3 – 5 5 – 7 7 – 9 9- 11 11 – 13	10 20 40 30 15	10 30 70 100 115
	Всего:	115

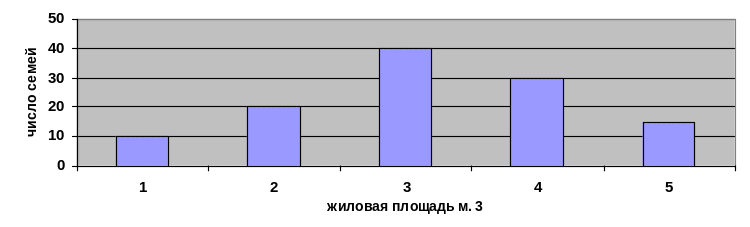
Рис. 7. Гистограмма распределения семей по размеру жилой площади, приходящейся на одного человека

Для графического изображения вариационных рядов может использоваться кумулятивная кривая. При помощи кумуляты изображается ряд накопленных частот. Накопленные частоты определяются путем последовательного суммирования частот по группам. Накопленные частоты показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение.

При построении кумуляты интервального вариационного ряда по оси абсцисс (х) откладываются варианты ряда, а по оси ординат (у) накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломаную линию, то есть кумуляту.

Используя данные накопленного ряда (табл. 2.5), построим кумуляту распределения (рис. 8.).

Рис. 8. Кумулята распределения семей по размеру жилой площади, приходящейся на одного человека

Если при графическом изображении вариационного ряда в виде кумуляты оси х и у поменять местами, то получим огиву.