2.6. Соотношение между высказываниями и соответствующими им множествами истинности

Мы рассмотрели такие множества истинности составных высказы­ваний, которые образованы посредством связок ∨,∧, . Все остальные связки можно определить через эти три основные и тем самым вывести, какие множества истинности им соответствуют. Например, известно, что импликация X→Y эквивалентна дизъюнкции ∨Y. Поэтому множе­ство истинности для X→Y будет тем же, что и множество истинности для ∨Y, т. е. оно будет иметь вид A∪B.

Если высказывание X логически ложно, то оно ложно в каждом логически возможном случае, и поэтому его множеством истинности будет пустое множество Ø.

Рассмотрим отношение следствия. Напомним, что из X следует У то­гда и только тогда, когда импликация X→Y логически истинна. Но высказывание X→Y тогда и только тогда логически истинно, когда его множество истинности совпадает с U, т. е. ( ) = U и А \ В = Ø. Но если А\В пусто, то В включает в себя А. Отношение включения обозначает­ся, как мы отмечали, А ⊂ В и читается «А является подмножеством В». Таким образом, высказывание X→Y логически истинно тогда и только тогда, когда А ⊂ В.

2.7 Абстрактные законы операций над множествами

Введенные операции над множествами подчинены некоторым очень простым абстрактным законам, которые будут перечислены в этом раз­деле.

Эти законы очень напоминают элементарные законы алгебры выска­зываний.

По этой причине множество, его подмножества и законы сочетания подмножеств образуют алгебраическую систему, называемую булевой ал­геброй. Система составных высказываний, подчиняющаяся таким зако­нам, тоже называется булевой алгеброй. Таким образом, любую из этих систем можно изучать или с алгебраической, или с логической точки зре­ния.

Ниже перечислены основные законы, действующие в булевых алгеб­рах.

1.A∪A=A

2.A∩A=A

3.A∪B=B∪A

4.A∩B=B∩A

5.A∪(B∪C)=(A∪B)∪C

6.A∩B(B∩C)=(A∩B) ∩C

7.A∩(B∪C)=(A∩B)∪(A∩C)

8.A∪(B∩C)=(A∪B) ∩(A∪C)

9.A∪U=U

10.A∩Ø=Ø

11.A∩U=A

12.A∪Ø=A

Законы для дополнений:

1.

2.A∪ =U

3.A∩ =Ø

4.

5.

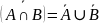
6.

Законы для разностей множеств:

1.A\B=A∩

2.U\A=

3.A\U=Ø

4.A\Ø=A

5.Ø\A=Ø

6.A\A=Ø

7.((A\B)\C)=A\(B∪C)

8.A\(B\C)=(A\B)∪(A∩C)

9.A∪(B\C)=(A∪B)\(C\A)

10.A∩(B\C)=(A∩B)\(A∩C)

2.8. Кортежи и декартовое произведение множеств

Определение. Пусть даны множества . Кортежем длины n, составленным из элементов этих множеств, называется конечная последовательность , где для всех k, , имеем .

Элемент называется k-й координатой или k-й компонентой кортежа α.

Два кортежа равны в том и только в том случае, когда они имеют одинаковую длину, причем их координаты, стоящие на местах с одина­ковыми номерами, равны, т. е. кортежи равны только в том случае, когда m=n, причем для всех 1≤k≤n.

Кортежи длины два называют упорядоченными парами, длины три — упорядоченными тройками,..., длины п — упорядоченными n-ками. Для краткости речи слово «упорядоченные» часто опускают.

Кортеж, не содержащий ни одной координаты, т. е. кортеж длины 0, называется пустым.

Основные отличия понятий кортежа и множества следующие:

а) в множестве порядок элементов не играет роли, а кортежи, отлича­ющиеся порядком элементов, различны, даже в случае, когда они имеют одинаковый состав;

б) в множестве все элементы различны, а в кортеже координаты могут повторяться.

В дальнейшем, чтобы различать множества и кортежи, будем элемен­ты множества заключать в фигурные скобки, а координаты кортежа — в угловые.

Пусть — некоторые множества. Их декартовым произве­дением называют множество, состоящее из кортежей вида ( ), где . Декартово произведение обозначается так: .