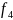- •1. Основы математической логики
- •1.1. Понятие составного высказывания
- •1.2. Логические операции над высказываниями
- •1.3. Логические отношения
- •1.4. Варианты импликации
- •1.5. Основные законы, определяющие свойства логических операций
- •1.6. Понятие булевой функции
- •1.7. Основные свойства элементарных булевых функций
- •1.8. Дизъюнктивные и конъюнктивные нормальные формы алгебры логики
- •Алгоритм построения
- •1.9. Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы
- •1.10. Многочлены Жегалкина
- •2. Множества и отображения
- •2.1. Понятие множества
- •2.2. Способы задания множеств
- •2.3. Подмножества
- •2.4 Операции над множествами
- •2.5. Соотношение между множествами и составными высказываниями
- •2.6. Соотношение между высказываниями и соответствующими им множествами истинности
- •2.7 Абстрактные законы операций над множествами
- •2.8. Кортежи и декартовое произведение множеств
- •2.9. Бинарные отношения
- •2.10. Отображение множеств
- •2.11. Функции
- •3. Логика предикатов или логика первого порядка
- •3.1. Предикаты
- •3.2. Применение предикатов в алгебре
- •3.3. Булева алгебра предикатов
- •3.4. Кванторы
- •3.5. Формулы логики предикатов
- •3.6. Равносильные формулы логики предикатов
- •3.7. Приведённые и нормальные формы в логике предикатов
- •3.8. Исчисление предикатов
- •4. Элементы теории алгоритмов
- •4.1. Вычислимые функции и алгоритмы
- •4.2. Свойства алгоритмов
- •4.3. Понятия разрешимого предиката, разрешимого множества, перечислимого множества
- •4.4. Пример алгоритма
- •4.5. Интуитивное понятие алгоритма
- •4.6.Теория рекурсивных функций. Простейшие функции
- •4.7. Операторы
- •4.8. Примитивно рекурсивные функции
- •4.9. Частично рекурсивные функции
- •4.10. Примитивно-рекурсивные предикаты
- •4.11. Нормальный алгоритм Маркова: основные понятия
- •4.12. Проблема слов в ассоциативном исчислении
- •4.13. Алгоритм в некотором алфавите а
- •4.14. Понятие нормального алгоритма
- •5. Примеры решения типовых задач. Задания для самостоятельного решения
- •5.1. Булевы функции. Таблицы истинности
- •Задания для самостоятельного решения
- •5.2. Равносильность булевых функций
- •Задания для самостоятельного решения
- •5.3. Преобразование булевых функций
- •Задания для самостоятельного решения
- •5.4. Функциональная полнота
- •Задания для самостоятельного решения
- •5.5. Булева алгебра. Нормальные формы
- •Задания для самостоятельного решения
- •5.6. Минимальные формы
- •Задания для самостоятельного решения
- •5.7. Алгебра Жегалкина
- •Задания для самостоятельного решения
- •5.8. Алгебра высказываний
- •Задания для самостоятельного решения
- •5.9. Предикаты
- •Задания для самостоятельного решения
- •5.10. Исчисление высказываний
- •Задания для самостоятельного решения
- •Список рекомендуемой литературы
1.5. Основные законы, определяющие свойства логических операций
Идемпотентность дизъюнкции и конъюнкции:

Коммутативность дизъюнкции и конъюнкции:
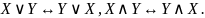
Ассоциативность дизъюнкции и конъюнкции:

Дистрибутивность операций дизъюнкции и конъюнкции относительно друг друга:

Двойное отрицание:

Закон де Моргана:

Склеивание:

Поглощение:

Действие с логическими константами 0 и 1:

Закон исключения третьего:

Тождество:

Отрицание противоречия:

Контрапозиция:

Цепное заключение:

Противоположность:

Модус поненс(modus ponens):

Сформулированные законы легко проверить с помощью таблицы истинности.
Заметим, что при исследовании различных высказываний на эквивалентность (равносильность) логическую связку ↔ можно заменить обычным знаком равенства =.
1.6. Понятие булевой функции
Булева функция, или функция алгебры логики, является одним из основных объектов дискретной математики.
Булевы функции названы в честь Дж. Буля, положившего начало применению математики в логике.
Функцию
 ,
принимающую
одно из двух значений 0 или 1, от п
переменных,
каждая из которых принимает одно из
двух значений 0 или 1, будем называть
булевой функцией
от п
переменных.
,
принимающую
одно из двух значений 0 или 1, от п
переменных,
каждая из которых принимает одно из
двух значений 0 или 1, будем называть
булевой функцией
от п
переменных.
Булева функция от п переменных сопоставляет каждому упорядоченному набору (кортежу), составленному из п элементов, 0 и 1, либо 1, либо 0.
Две
булевы функции называются равными, если
для любых одинаковых наборов значений
переменных обе функции принимают
одинаковые значения. Булевых функций
одной переменной четыре, а двух переменных
— шестнадцать и т.д. Число булевых
функций от п
переменных
равно
 .
.
Рассмотрим функции одной и двух переменных, которые называются «элементарными» функциями и с помощью которых можно определить функции большего количества переменных.
Рассмотрим таблицы истинности таких функций.
Таблица истинности булевой функции одной переменной:
x |
|
|
|
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
Функции и называются константами — соответственно 0 и 1.
Функция
совпадает
с переменной х
и
называется тождественной
 .
.
Функция
принимает значения, противоположные
значениям аргумента х,
и
называется отрицанием х,
обозначается
 .
.
Таблица истинности булевой функции двух переменных:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
Следует отметить, что здесь к функциям двух переменных относятся и такие, которые в действительности зависят от одной переменной.
1. Функции и представляют собой константы 0 и 1.
2.
Функции
,
,
,
существенно зависят только от одной
переменной:
 .
.
3. Остальные функции существенно зависят от двух переменных, и для них есть названия и обозначения:
а)
функция
 и
называется конъюнкцией,
и
называется конъюнкцией,
б)
функция
 и называется дизъюнкцией,
и называется дизъюнкцией,
в)
функция
 и называется эквивалентностью,
и называется эквивалентностью,
г)
функция
 называется суммой по модулю два, или
суммой Жегалкина,
называется суммой по модулю два, или
суммой Жегалкина,
д)
функция
 и называется конверсией,
и называется конверсией,
е)
функция
 и называется импликацией,
и называется импликацией,
ж)
функция
 и называется штрих Шеффера,
и называется штрих Шеффера,
з)
функция
 и называется стрелкой Пирса,
и называется стрелкой Пирса,
и)
функции
 логически несовместимы с импликацией
и конверсией и называются функциями
запрета.
логически несовместимы с импликацией
и конверсией и называются функциями
запрета.