Задания для самостоятельного решения
5.39. Построить минимальные ДНФ и КНФ, используя карты Карно и метод Квайна, если функции а)f(x,y,z) и б)f(x1,x2,x3,x4) заданны вектором своих значений
1. а) (1000 1111); б) (1100 1101 0011 0011);
2. а) (1010 0101); б) (1111 1100 1011 1011);
3. а) (0011 1100); б) (1101 0011 1101 0011);
4. а) (1100 0101); б) (1110 0101 0011 0101);
5) а) (1011 1100); б) (1100 1011 1111 1011);
6) а) (0101 0011); б) (0101 0101 1110 0011);
7) а) (1111 1011); б) (0011 0011 1101 1101);
8) а) (0101 1001); б) (1011 1011 1100 1111);
9) а) (0011 1101); б) (0101 0011 0101 1110);
10) а) (1110 0011); б) (0011 1101 0011 1100);
11) а) (0010 0011); б) (0111 0010 1011 1111);
12) а) (1000 0011); б) (0000 1111 0101 1100);
13) а) (1100 0010); б) (1111 0111 0101 1101);
14) а) (1110 0101); б) (0101 1101 0101 0000);
15) а) (0000 1111); б) (0110 0011 0101 1110);
16) а) (1100 1011); б) (1010 1010 1001 1100);
17) а) (0000 1011); б) (1100 0011 0011 1010);
18) а) (1011 1011); б) (1111 1111 0101 0100);
19) а) (1111 0001); б) (1000 0011 1111 0000);
20) а) (1000 0000); б) (0000 0000 0101 1101).
5.40. Построить минимальные ДНФ и КНФ, используя карты Карно.
5.41. Построить минимальные ДНФ, используя метод Квайна.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
5.42. Построить минимальную ДНФ, КНФ методом Квайна если:
1. f(1,0,0)= f(1,1,0)= f(1,0,1)= f(1,1,1)= f(0,0,0)=1.
2. f(1,1,1)= f(1,1,0)= f(1,0,1)= f(0,0,0)=1.
3. f(1,1,0)= f(1,0,1)= f(0,1,1)= f(1,0,0)=1.
4. f(1,0,0)= f(1,1,1)= f(1,0,1)=1.
5. f(1,0,1)= f(1,1,0)= f(0,0,1)= f(1,1,1)= f(0,0,0)= f(1,0,0)=1.
6. f(1,1,1)= f(1,1,0)= f(1,0,1)= f(0,0,1)= f(0,0,0)=1.
7. f(1,0,0)= f(1,1,0)= f(0,0,0)=1.
8. f(1,0,0)= f(1,0,1)= f(1,1,1)=1.
9. f(1,1,0)= f(1,0,1)= f(1,1,1)= f(0,0,1)=1.
10. f(1,1,1)= f(1,1,0)= f(1,0,1)= f(0,1,1)= f(0,0,0)= f(0,1,0)= f(0,0,0)=1.
11. f(1,0,0,1)= f(1,0,0, 0)= f(1,0,1,0)= f(1, 1,0, 1)= f(1,1,0,0)=1.
12. f(1,0,0, 0)= f(1,0,1,0)= f(1, 1,0, 1)= f(1,1,0,0)=1.
13. f(0,0,0,1)= f(1,0,0, 0)= f(1,0,1,0)= f(1, 1,0, 1)= f(1,1,0,0)=1.
14. f(1,0,0, 0)= f(1,0,1,0)= f(1, 1,0, 1)= f(1,1,0,0)=1.
15. f(1,0,0,1)= f(1,0,0, 0)= f(1,0,1,0)= f(1, 1,0, 1)= f(1,1,0,0)= f(1,1,0,0)= =f(0,1,0,1)=f(1,1,1,1)=1.
16. f(1,0,0, 0)= f(1,0,1,0)= f(1, 1,0, 0)= f(1,1,0,1)=1.
17. f(1,0,0,1)= f(1, 1,0, 1)= f(1,1,0,0)= f(1,0,0, 0)= f(1,0,1,0)= f(0, 1,0, 1)=
=f(1,0,0,0)=1.
18. f(0,0,0,1)= f(1,0,0, 0)= f(0,0,1,0)= f(1,0,0, 1)= f(0,1,0,0)=1.
19.f(1,0,0, 0)= f(1, 1,0, 0)= f(1,1,1,0)= f(1,0,0, 1)= f(1,0,1,0)= f(1, 1,0, 1)=
=f(0,1,0,0)=1.
20. f(1,1,1,1)= f(1,1,0, 0,)= f(1,0,1,0)= f(1, 1,0, 1)= f(0,1,0,0)=1.
5.43. Построить сокращенную ДНФ по заданной КНФ:
1.
2.
3.
4.
5.
6.
7.
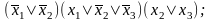
8.
9.
10.
5.7. Алгебра Жегалкина
Множество булевых
функций, заданных в базисе Жегалкина
называется алгеброй Жегалкина.
Основные свойства.
1.
коммутативность
;
2.
ассоциативность
;
3.
дистрибутивность
;
4.
свойства констант
;
5.
.
Утверждение 7.1. Через операции алгебры Жегалкина можно выразить все другие булевы функции:
Определение. Полиномом Жегалкина (полиномом по модулю 2) от n переменных называется выражение вида
где постоянные
могут принимать значения 0 или 1.
Если полином Жегалкина не содержит произведений отдельных переменных, то он называется линейным (линейная функция).
Теорема 7.1. Каждая булева функция представляется единственным образом в виде полинома Жегалкина.
Основные методы построения полиномов Жегалкина:
1. Метод, основанный на преобразовании формул. Используя утверждение 7.1. приводим формулу к виду содержащему связки из базиса S={⊕,&,1}; раскрываем скобки используя закон дистрибутивности (см. свойство 3); а затем применяем свойства 4 и 5.
2. Метод неопределенных коэффициентов. Полином Жегалкина, реализующий заданную функцию ищем в виде
Найдем коэффициенты . Для этого последовательно придадим переменным значения из каждой строки таблицы истинности. В итоге получим систему из уравнений с неизвестными, имеющую единственное решение. Решив ее, находим коэффициенты
полинома
Пример 5.28. Построить полином Жегалкина функции
a)
б)
Решение.
а) 1 способ. Запишем искомый полином в
виде
Пользуясь таблицей истинности
-
0
0
1
1
0
1
0
1
1
1
0
1
получаем, что
Откуда
последовательно находим,
Следовательно,
2 способ (метод преобразования формул.) Имеем
б) 1 способ. Пусть полином Жегалкина имеет вид:
(т.к.
).
(т.к.
)
Итак, получаем полином Жегалкина 3-й степени.
Пример
5.29. Построить
полином Жегалкина для функции
методом неопределенных коэффициентов.
Является ли
линейной.
Решение. Ищем полином Жегалкина в виде:
Используя таблицу истинности для , имеем
Итак,
–
не линейна.