10. Прогноз в моделях линейной регрессии.
Вернемся
к рассматриваемому примеру. Мы имеем
ряд значений независимой переменной x
(затраты на рекламу) и зависимой переменной
у
(доход от продажи продукции). На основании
этих данных мы построили линейную
модель. Поскольку модель адекватна, то
можно прогнозировать изменение объема
продажи продукции в зависимости от
изменения затрат на рекламу. При этом
можно получить два типа прогноза:
точечный и интервальный. Точечный
прогноз дает значение зависимой
переменной для соответствующего значения
на основании построенной модели
.
При этом, исходя из общей модели, действительное значение у для прогноза равняется
,
где
– значение случайной величины.
Таким
образом, значение прогноза
является оценкой истинного значения
переменной
.Полученный
прогноз является точечной оценкой.
Исходя из полученного точечного прогноза,
можно построить доверительный интервал,
в который с заданной вероятностью
попадает истинное значение зависимой
переменной. Такой доверительный интервал
при заданном уровне значимости
находится по формуле
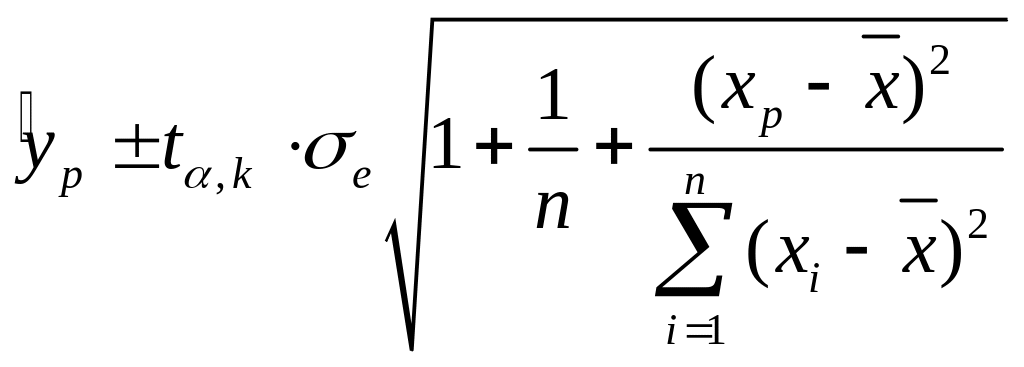(1.24)
где
– значения критерия Стьюдента при
заданном уровне значимости
и числе степеней свободы
,
– дисперсия ошибок,
.
Обратим внимание, что доверительный интервал становится шире по мере удаления х от своего среднего значения, так как, чем дальше от центра, тем меньше уверенность в значении спрогнозированного значения y.
На практике больше используется построение доверительного интервала для математического ожидания , т.е. доверительный интервал для
.
Формула доверительного интервала для промежуточных значений имеет вид:
(1.25)
Пример 4. Продолжим рассмотрение зависимости объема реализации продукции от затрат на рекламу. Напомним, что построенная модель имеет вид .
Найдем
значение прогноза объема реализации
продукции при затратах на рекламу
: 
.
Построим доверительный интервал
зависимой переменной. Дисперсию ошибок
мы находили в предыдущем примере:
.
Заметим, что
.
При уровне значимости
и числу степеней свободы
по таблице распределения Стьюдента
находим
.
Таким образом,
.
Доверительный
интервал имеет вид
т.е.
или
.
Глава II. Нелинейная парная регрессия.
1. Квазилинейное уравнение регрессии.
Наиболее распространенной моделью в экономике является линейная регрессия. Однако не все экономические процессы можно ею моделировать. Поэтому на практике используются и более сложные модели с нелинейной зависимостью между показателем у и фактором х. По методике оценки параметров рассматриваются парные нелинейные регрессии двух видов: 1) нелинейные по факторам, но линейные по неизвестным параметрам, которые подлежат оценке; 2) нелинейные по факторам и параметрам.
Регрессии, нелинейные по факторам, но линейные по оцениваемым параметрам, называются квазилинейными.
Парную квазилинейную регрессию можно записать в общем случае следующим образом
.
Заменой
переменной
нелинейная парная регрессия сводится
к линейной парной регрессии
.
Коэффициент эластичности в экономике определяется по формуле
.
Он означает на сколько процентов изменится показатель у, если фактор х изменится на 1%. Для квазилинейного уравнения регрессии формула принимает вид
.
Рассмотрим ряд частных случаев парной квазилинейной регрессии.
1.
Уравнение регрессии
заменой переменной
сводится к линейному уравнению регрессии
.
Коэффициент эластичности вычисляется
по формуле
.
2.
Уравнение регрессии
заменой
сводится к линейному уравнению регрессии
.
Коэффициент эластичности вычисляется
по формуле
.
3.
Уравнение регрессии
заменой переменной
сводится к линейному уравнению регрессии
.
Коэффициент эластичности вычисляется
по формуле
.
4.
Уравнение регрессии
заменой переменной
сводится к линейному уравнению регрессии
.
Коэффициент эластичности вычисляется
по формуле
5.
Уравнение регрессии
заменой
сводится к линейному уравнению регрессии
.
Коэффициент эластичности вычисляется
по формуле
.
6.
Аналогичным образом уравнение
заменой
сводится к линейному уравнению регрессии
.
Коэффициент эластичности вычисляется
по формуле
.
7.
Рассмотрим регрессию нелинейную по
показателю
.
Перепишем уравнение в виде
.
Заменой
уравнение сводится к линейному
.
Коэффициент эластичности вычисляется
по формуле
.
8.
Более сложной, с точки зрения замены
переменных, является уравнение регрессии
вида
.
В
этом случае необходимо сделать замену
обеих переменных
,
.
Тогда нелинейное уравнение регрессии
сведется к линейному
.
Коэффициент эластичности находится по
формуле
.