
Конспект+лекций+Імовірнісні+основи+обробки+данних (1)
.pdf
Тема: «Предмет теорії ймовірностей».
Детермінованість
Будь-яка точна наука вивчає не самі явища, а їх моделі. При цьому побудови математичної моделі реального явища достатньо враховувати тільки основні закономірності, які дозволяють побачити результат досліду.
Виявлені закономірності і явища називаються детерміністичними (тобто виявлені).
Ймовірнісність
Виявлені в випадкових дослідженнях закономірності називають статистичними (або ймовірнісними). Статистичні закономірності досліджуються методами теорії ймовірностей та математичної статистики.
Історія розвитку теорії ймовірності
Перші роботи, у яких зароджувалися основні поняття теорії ймовірностей, являли собою спроби створення теорії азартних ігор (Кардано, Гюйгенс, Паскаль, Ферма й інші в XVI-XVII вв.).
Наступний етап розвитку теорії ймовірностей зв'язаний з ім'ям Якоба Бернуллі (1654—1705). Доведена ним теорема, що одержала згодом назву «Закону великих чисел», була першим теоретичним обґрунтуванням накопичених раніше фактів. Подальшими успіхами теорія ймовірностей зобов'язана Муавру, Лапласові, Гаусу, Пуассонові й ін.
Новий, найбільш плідний період зв'язаний з іменами П.Л. Чебишева (1821 —1894) і його учнів А.А. Маркова (1856—1922) і А.М. Ляпунова (1857—1918). У цей період теорія ймовірностей стає стрункою математичною наукою. Її наступний розвиток зобов'язаний у першу чергу російським і радянським математикам (С.Н. Бернштейн, В.И. Романовский, А.Н. Колмогоров, А.Я. Хинчин, Б.В. Гнеденко, Н.В. Смирнов і ін.). В даний час ведуча роль у створенні нових галузей теорії ймовірностей також належить радянським математикам.
Предмет теорії ймовірностей
Теорія ймовірностей — це математична наука, що вивчає закономірності, притаманні масовим випадковим явищам. При цьому предмет теорії ймовірностей розглядає не самі явища, а їх спрощені схеми — математичні моделі.
Предмет теорії ймовірностей є математична модель випадкових явищ.
Мета теорії ймовірностей — здійснення прогнозу в області випадкових явищ, вплив на хід цих явищ, контроль їх, обмеження сфери дії випадковостей.
Випадкові події та їх класифікації
Якщо проводиться деякий дослід (експеримент, спостереження, дослідження), результатом якого передбачити заздалегідь неможливо в теорії ймовірностей називають
випадковими.
Випадковою подією називають будь-який результат, який може відбутися, а може й не відбутися.
Розглянемо падіння гральної кістки: Позначимо події так:
А — випадання 2 очок; В — випадання непарного; С — випадання 10 очок;
D — випадання цілого число очок; Е — випадання не більше 4 очок.
1

Безпосередні взаємовиключні результати досліду називають елементарною подією і позначають ωі (і=1,2,3…).
Кожній випадковій події відповідає певна множина можливих подій Ω. Безліч всіх елементарних подій називають простором елементарних подій або простором результатів і позначають Ω (ω-омега). В кістках: всього 6 простих випадків.
i={1,2,3,4,5,6}.
Ω={x1, x2, x3, x4, x5, x6}.
Подія називається достовірною, якщо воно обов’язковою настане в разі досліду (позначають Ω).
Подія називається неможливою, якщо вона не станеться в разі досліду (позначають
Ø).
Дві події називаються несумісними, якщо поява однієї з них не включає появу іншої в тому ж досліді, тобто вони не зможуть відбутися в 1-му досліді. В іншому випадку події називаються сумісними.
Але, якщо одну й ту саму випадкову подію виконувати багато разів при однакових умовах, то можна виявити деяку закономірність появи цієї події, яку називають
імовірною закономірністю масових однорідних випадкових подій.
Сумою (об'єднанням) (amount) двох подій A i В називають подію С, яка полягає в тому, що в одному досліді відбудеться або подія А, або В, або обидві разом. Суму записують так:
С=А+В або  .
.
Добутком (перетином) (product) двох подій A i В називають подію С, яка полягає в тому, що відбувається і подія А, і подія В одночасно, це записують:
С=АВ або 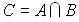 .
.
Узагальнюючи цi операції для кількох подій, матимемо
 ,
, 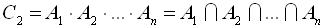 .
.
Різницею двох подій A i В називають подію С, яка настає тоді коли А вже настала, а В - ще не настала, i це записують: А-В=С, або А=В+С. Вірогідні події позначають
буквою U, а неможливі V. Тому 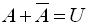 ,
, 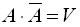 ; для несумісних A i В: AB=V. А — випадання 2 очок => Подія А={2}.
; для несумісних A i В: AB=V. А — випадання 2 очок => Подія А={2}.
В — випадання парного числа очок => Подія В={1,3,5}.
Е— випадання не більше 4 очок => Подія А={1,2,3,25,5}???.
АА {1,3};
B - E {5};
А {1.3,3,5,6};
BD;
CØ.
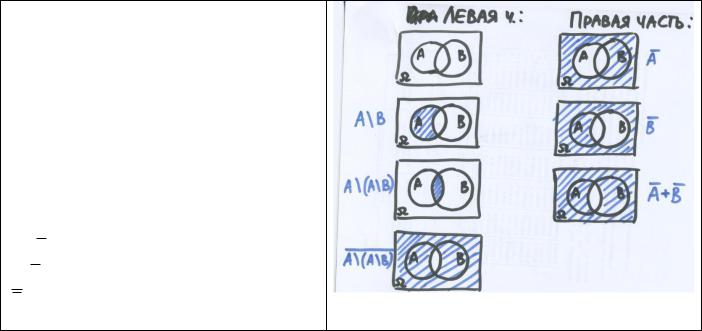
Події та дії над ними можна наочно ілюструвати за допомогою діаграм Ейлера-
Вена:
Достовірна подія зображується прямокутником;
Елементарні події зображуються точками;
Випадкова подія зображується областю в середині нього.
2
A B B A A B B A
( A B) C A C B C ( A B) C A (B C) ( A B) C A (B C)
A B A
A A A
A
A A
A A
A A Ø
A A
3
Тема: «Випадкова велечина».
Випадкова величина
Одним iз найважливiших понять теорiї ймовiрностей є поняття про випадковi величини.
Випадковою величиною називається величина, яка в результатi дослiду може прийняти те чи iнше значення, при цьому заздалегiдь невiдомо, яке саме.
Приклади випадкових величин:
число влучень при трьох пострiлах;
число викликiв, що надходили на телефонну станцiю за добу;
частота влучення при 10 пострiлах.
Увсiх трьох наведених прикладах випадковi величини можуть приймати окремi (iзольованi) значення, якi можна заздалегідь перерахувати.
Так,
в прикладi 1) цi значення: 0, 1, 2, 3;
в прикладi 2): 1, 2, 3, 4,...;
в прикладi 3): 0; 0,1; 0,2; ...;1,0.
Iснують випадковi величини iншого типу, наприклад:
абсциса точки влучення при пострiлi;
помилка зважування тiла на аналiтичних вагах;
швидкiсть лiтака в момент виходу на задану висоту;
вага навмання взятого зерна пшеницi i т.д.
Можливi значення таких випадкових величин не вiдокремленi один вiд одного; вони безперервно заповнюють певний промiжок, який iнодi має рiзко вираженi межi, а частiше - невизначенi, розпливчастi границi.
Такi випадковi величини, можливi значення яких безперервно заповнюють певний промiжок, називаються безперервними випадковими величинами.
Якщо "класична"теорiя ймовiрностей оперувала переважно з подiями, то сучасна теорiя ймовiрностей має справу з випадковими величинами.
Наведемо приклади типових для теорiї ймовiрностей прийомiв переходу вiд подiй до випадкових величин.
Здiйснюється дослiд (випробування), в результатi якого може з’явитися або нi деяка подiя A.
Замiсть подiї можна розглянути випадкову величину x, яка дорiвнює 1, якщо подiя A вiдбувається, i дорiвнює 0, якщо подiя не вiдбувається.
Випадкова величина x, очевидно, є дискретною; вона має два можливих значення:
0 i 1.
Ця випадкова величина називається характеристичною випадковою величиною
подiї A.
На практицi часто замiсть подiй виявляється зручніше оперувати їх характеристичними випадковими величинами.
Наприклад, якщо проводиться декiлька випробувань (дослiдiв), в кожному з яких можлива поява подiї A, то загальне число появ цiєї подiї дорiвнює сумi характеристичних випадкових величин подiї A в усiх дослiдах.
З iншого боку, дуже часто для обчислення ймовiрностi подiї виявляється зручно пов’язати цю подiю з якоюсь безперервною випадковою величиною (або системою безперервних величин).
Так, наприклад, вимiрюються координати будь-якого об’єкту.
4

Класичне визначення ймовiрностi.
Cукупнiсть подiй утворює повну групу подiй для даного випробування, якщо його результатом обов’язково стає хоча б одне з них.
Наведемо приклади повних груп подiй:
випадiння герба i випадання решки (цифри) при одному киданнi монети;
влучення в цiль i промах при одному пострiлi;
випадання одного, двох, трьох, чотирьох, п’яти i шести очок при одному киданнi гральної кiстки.
Розглянемо повну групу попарно несумiсних подiй x1, x2,...,xn, пов’язану з деяким випробуванням.
Припустимо, що в цьому випробуваннi здiйснення кожної з подiй xi (i = 1, 2,...,n) рiвноможливе, тобто умови випробування не створюють переваги появi якої-небудь подi перед iншими можливими.
Подiї x1, x2,...,xn, що утворюють повну групу попарно несумiсних i рівно можливих подiй, називають елементарними подiями.
До прикладу випробування з пiдкиданням гральною кiстки. xi - подiя, яка полягає у тому, що кiстка випала гранню з цифрою i.
Подiї x1, x2,...,x6 утворюють повну групу попарно несумiсних подiй.
Оскiiльки гральна кiстка передбачається однорiдною i симетричною, то події x1, x2,...,x6 є рiвноможливими, тобто елементарними.
Класичне визначення ймовiрностi
Ймовiрнiстю P(A) подiї A називається спiввiдношення m числа елементарних подiй, що сприяють подiї A, до числа N всіх елементарних подiй, Тобто P(A) mN
З наведеного класичного визначення ймовiрностi випливають наступнi її властивостi.
Iмовiрнiсть достовiрної подiї дорiвнює одиницi.
Дiйсно, достовiрнiй подiї повиннi сприяти всi N елементарних подiй, тобто m = N i, отже, P(A) mN NN 1
Iмовiрнiсть неможливо¨ı подi¨ı дорiвнює нулю.
Справдi, неможливiй подi¨ı не може сприяти жодна з елементарних подiй, тобто m
= 0, звiдки, P( A) Nm N0 0
Ймовiрнiстю випадкової подiї є позитивне число мiж нулем та одиницею. Дiйсно, випадковiй подiї сприяє лише частина iз загальногочисла елементарних
подiй. Тому в цьому випадку 0 < m < N, значить, 0 mN 1, Отже, 0 ≤ P(A) ≤ 1.
Тому, ймовiрнiсть будь-якої подiї задовольняє подвiйну нерiвнiсть.
З визначення ймовiрностi випливає, що елементарнi подiї є рiвноiмовiрними, тобто мають одну й ту саму iмовiрнiсть.
Застосування елементiв комбiнаторики до знаходження iмовiрностей
Комбiнаторика - роздiл математики, що вивчає питання про те, скiльки комбiнацiй певного типу можна скласти з даних предметів (елементiв). Як при вирiшеннi задач з використанням класичного визначення ймовiрностi, так i надалi нам знадобляться деякi формули комбiнаторики.
Наведемо найбiльш уживанi з них.
5
Комбінаторика
Якщо з безлiчi предметiв обирається деяка пiдмножина, то її називають
вибiркою.
Вибiрки бувають впорядкованi i невпорядкованi.
У впорядкованiй вибiрцi суттєвим є порядок, в якому слідують її елементи, iншими словами, змiнивши порядок елементiв, ми отримаємо iншу вибiрку.
Наприклад,
iз цифр 1, 2, 3, 4, 5 можна скласти наступнi тризначнi числа
123, 431, 524, ... i т.д.
Це впорядкованi трьохелементнi вибiрки, оскiльки 123 i 132 - рiзнi числа.
Або iнший приклад:
з 30-ти однакових деталей обрати двi - будь-яка пара деталей являє собою неупорядковану двохелементу вибiрку, оскiльки їх порядок не важливий.
Розміщення
Розмiщеннями з n рiзних елементiв по m елементiв (m ≤ n) називаються комбiнацiї, складенi з даних n елементiв по m елементiв, якi вiдрiзняються або самими елементами, або порядком елементiв.
Число розмiщень без повторень з n по m (n рiзних елементiв) обчислюється за
формулою: |
Am |
n! |
|
||
|
||
|
n |
(n m)! |
|
|
Розмiщеннями з повтореннями iз n елементiв по m називаються впорядкованi m- елементнi вибiрки, в яких елементи можуть повторюватися.
Число розмiщень з повтореннями обчислюється за формулою: A~nm nm
Наприклад, розглянемо, як iз трьох елементiв a,b,c можна скласти розмiщення по два елементи :
без повторень
ab, ac, bc, ba, ca, cb
(за формулою ( Am |
n! |
|
|
) A2 |
|
|
3! |
|
6, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
n |
(n m)! |
3 |
|
(3 2)! |
|
||||
|
|
|
|
||||||
з повтореннями |
|
|
|
|
|
|
|
|
|
aa, bb, cc, ab, ac, bc, ba, ca, cb |
|
|
|
||||||
~ |
|
~ |
|
32 |
9 |
|
|
|
|
(за формулою ( Am nm ) |
A2 |
|
|
|
|||||
n |
|
3 |
|
|
|
|
|
|
|
Перестановки
Перестановками з n рiзних елементiвназиваються розмiщення з цих n елементiв по
n.
Перестановки можна вважати окремим випадком розміщень при m = n. Отже, число всiх перестановок iз n елементiв без повторень обчислюється за
формулою: Pn = n(n − 1)(n − 2)... · 2 · 1 = n!
Число перестановок з повтореннями (k рiзних елементiв, де елементи можуть повторюватися m1, m2, ..., mk раз i
m1 + m2 + ... + mk = n, де n - загальна кiлькiсть елементiв)
~ |
|
,..., mk ) |
|
n! |
|
обчислюється за формулою: Pn |
(m1, m2 |
|
|
||
m1 |
!m2!...mk ! |
||||
|
|
|
Розглянемо попереднiй приклад, коли є три елементи a,b,c. Якi перестановки з цих букв можна отримати i скiльки таких наборiв вийде, якщо:
6

лiтери в наборi не повторюються;
лiтера a повторюється два рази? Розв’язок
Упершому випадку вийдуть набори: abc, acb, bac,bca, cab, cba. За формулою (Pn = n!) маємо P3 = 3! = 6.
Удругому випадку вийдуть набори:
aabc, aacb, baca,bcaa, caab, cbaa, abac, acab, abca, acba, baac, caab.
~ |
|
) |
|
n! |
|
~ |
|
|
4! |
|
12 |
|
За формулою ( Pn |
(m1 , m2 ,..., mk |
|
|
|
) маємо P4 |
(2,1,1) |
|
|
||||
m1 |
!m2 !...mk |
! |
2!1!1! |
|||||||||
|
|
|
|
|
|
|
||||||
Поєднання
Поєднаннями (сполученнями) з n елементiв по m елементiв називаються комбiнацiї, складенi з даних n елементiв по m елементiв, якi рiзняться хоча б одним елементом.
Вiдмiннiсть сполучень вiд розмiщень в тому, що в сполученнях не враховується порядок елементiв.
Число поєднань (сполучень) без повторень (n рiзних елементiв, узятих по m) обчислюється за формулою:
С m |
n! |
|
|
|
|
n |
m!(n m)! |
|
Числа Сnm є коефiцiєнтами у формулi бiнома Ньютона
( p q)n pn Cn1 pn 1q Cn2 pn 2q2 ... qn i тому часто називаються біноміальними
коефiцiєнтами, якi можна знайти за допомогою трикутника Паскаля.
Число сполучень c повтореннями (n елементiв, узятих по m, де елементи в наборi
~m |
|
(n m 1)! |
|
можуть повторюватися) обчислюється за формулою Сn |
|
||
m!(n 1)! |
|||
|
|
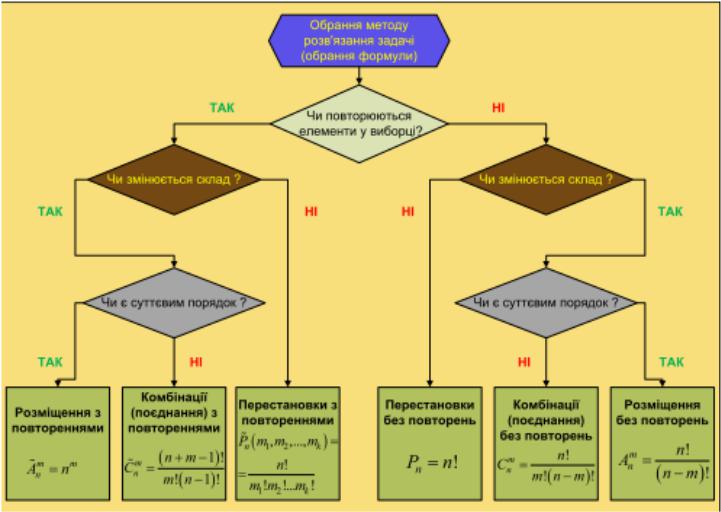
Схема визначення формули
7
8
