
Формулы к мод
.docxОбчислення роботи виходу для металу з урахуванням цих сил приводить до наступного результату
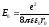 . (1.1)
. (1.1)
Звідси видно, що робота виходу для металів зменшується зі збільшенням міжатомної відстані. Величина роботи виходу виміряється декількома електрон-вольтами. Значення роботи виходу для основних речовин, що використовуються для створення катодів приведені в таб.1.
Величина
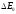 зменшення роботи виходу залежить не
тільки від фізичних властивостей керна
та активатора, а також і від товщини
адсорбованого шару. Найбільша величина
зменшення роботи виходу залежить не
тільки від фізичних властивостей керна
та активатора, а також і від товщини
адсорбованого шару. Найбільша величина
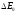 виходить при нанесенні одноатомного
шару. Так, наприклад, для вольфраму,
активованого барієм,
виходить при нанесенні одноатомного
шару. Так, наприклад, для вольфраму,
активованого барієм,
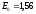 еВ,
а при активуванні вольфраму торієм
еВ,
а при активуванні вольфраму торієм
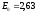 еВ.
еВ.
Тоді по
осі ординат відкладається величина
потенціалу
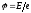 .
.
Струм з
одиниці поверхні катода – питомий струм
термоелектронної емісії визначається
вираженням (формулою Ричардсона-Дешмона):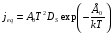
, (1.2)
де
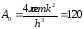 А/см2град
– стала термоелектронної емісії або
стала Зоммерфельда; DS
– коефіцієнт Шотки, що визначає прозорість
потенційного бар’єру для електронів;
e,
m
– заряд та маса електрона, відповідно;
h,
k
– сталі Планка та Больцмана, відповідно.
А/см2град
– стала термоелектронної емісії або
стала Зоммерфельда; DS
– коефіцієнт Шотки, що визначає прозорість
потенційного бар’єру для електронів;
e,
m
– заряд та маса електрона, відповідно;
h,
k
– сталі Планка та Больцмана, відповідно.
Експериментальна
перевірка формули (1.2) приводить до інших
величин цієї постійної: для різних
речовин стала
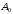 може приймати значення від 10 до 300. Данні
для основних матеріалів приведені в
таб.2.
може приймати значення від 10 до 300. Данні
для основних матеріалів приведені в
таб.2.
Таблиця 2
|
Метал |
W |
Mo |
Ta |
Th |
Ba |
Cs |
|
А0, А*м-2 *К-2 *106 |
60 |
55 |
60 |
70 |
60 |
162 |
|
Е0/k , K*103 |
52,4 |
48,1 |
47,5 |
39,2 |
24.5 |
2,1 |
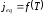 носить експонентний характер. На рис.1.3
показані якісні криві зміни струму
емісії від температури для двох катодів
площею 0,03см2,
але з різною роботою виходу.
носить експонентний характер. На рис.1.3
показані якісні криві зміни струму
емісії від температури для двох катодів
площею 0,03см2,
але з різною роботою виходу.
Якщо
електроду
 надати позитивний потенціал
надати позитивний потенціал
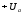 ,
крива зміни енергії приймає, вид,
показаний на рис.1.4б. При цьому енергетичний
бар'єр на поверхні катода зменшується
на величину
,
крива зміни енергії приймає, вид,
показаний на рис.1.4б. При цьому енергетичний
бар'єр на поверхні катода зменшується
на величину
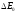 .
Обчислення цієї величини показує, що
вона залежить від напруженості зовнішнього
поля згідно
.
Обчислення цієї величини показує, що
вона залежить від напруженості зовнішнього
поля згідно
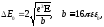 (1.3)
(1.3)
де
 – напруженість електричного поля,
– напруженість електричного поля,
 і
і
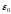 – діелектричні проникність середовища
та діелектрична стала, відповідно. З
урахуванням зовнішнього електростатичного
поля, питомий струм термоелектронної
емісії можна записати у вигляді
– діелектричні проникність середовища
та діелектрична стала, відповідно. З
урахуванням зовнішнього електростатичного
поля, питомий струм термоелектронної
емісії можна записати у вигляді
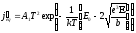 . (1.4)
. (1.4)
Збільшення струму емісії в результаті впливу зовнішнього прискорювального електростатичного поля називається ефектом Шоттки.
Щільність
струму тунельної емісії
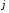 становить частину щільності потоку
електронів
становить частину щільності потоку
електронів
 ,
що падають зсередини провідника на
бар'єр і визначається прозорістю бар'єра
,
що падають зсередини провідника на
бар'єр і визначається прозорістю бар'єра
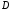 :
:
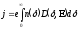 , (1.5)
, (1.5)
де
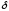 – частка енергії електрона, пов'язана
з компонентом його імпульсу, нормальним
до поверхні емітера (енергетичний
спектр);
– частка енергії електрона, пов'язана
з компонентом його імпульсу, нормальним
до поверхні емітера (енергетичний
спектр);
 – напруженість електричного поля на
поверхні;
– напруженість електричного поля на
поверхні;
 – заряд електрона;
– заряд електрона;
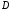 – прозорість енергетичного бар’єру,
який залежить від його висоти і форми.
– прозорість енергетичного бар’єру,
який залежить від його висоти і форми.
Найбільш
повно вивчена тунельна емісія металів
у вакуум. У цьому випадку величина
щільності струму польової емісії
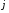 визначається законом Фаулера - Нордхейма:
визначається законом Фаулера - Нордхейма:
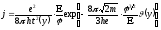 , (1.6)
, (1.6)
де
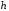 — постійна Планка,
— постійна Планка,
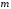 — маса електрона,
— маса електрона,
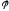 — потенціал роботи виходу металу,
— потенціал роботи виходу металу,
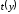 і
і
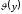 — табульовані функції аргументу
— табульовані функції аргументу
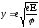 .
Підставивши значення констант і поклавши
.
Підставивши значення констант і поклавши
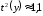 ,
а
,
а
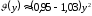 ,
одержимо з формули (1.6) наближене
співвідношення:
,
одержимо з формули (1.6) наближене
співвідношення:
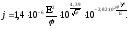 , (1.7)
, (1.7)
(величини
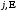 і
і
 відповідно в A/см2,
B/см і В).
відповідно в A/см2,
B/см і В).
Формула
(1.6) отримана для випадку нульової
температури
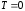 К
і що поза металом, під час відсутності
поля, на електрони діють тільки сили
дзеркального зображення. Форма
потенційного бар'єра для цього випадку
показана на мал.1.4,б. Прозорість бар'єра
К
і що поза металом, під час відсутності
поля, на електрони діють тільки сили
дзеркального зображення. Форма
потенційного бар'єра для цього випадку
показана на мал.1.4,б. Прозорість бар'єра
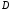 може бути розрахована по методу Венцеля
– Крамерса - Бриллюэна. Незважаючи на
спрощення, теорія Фаулера-Нордхейма
добре співпадає з експериментом.
може бути розрахована по методу Венцеля
– Крамерса - Бриллюэна. Незважаючи на
спрощення, теорія Фаулера-Нордхейма
добре співпадає з експериментом.
На
практиці вимірюють залежність струму
 (
(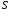 — площа поверхні, що емітує) від
— площа поверхні, що емітує) від
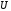 напруги
напруги
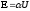 (
(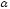 -
так званий польовий множник). Тунельна
емісія металів характеризується високими
граничними густинами струму до величин
-
так званий польовий множник). Тунельна
емісія металів характеризується високими
граничними густинами струму до величин
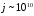 A/см2,
що пояснюється теорією Фаулера - Нордхейма.
Лише при
A/см2,
що пояснюється теорією Фаулера - Нордхейма.
Лише при
 A/см2
мають місце відхилення від формули
(1.6), пов'язані із впливом об'ємного заряду
або з особливостями форми потенційного
бар'єра поблизу поверхні металу.
Необмежене підвищення напруги приводить
при
A/см2
мають місце відхилення від формули
(1.6), пов'язані із впливом об'ємного заряду
або з особливостями форми потенційного
бар'єра поблизу поверхні металу.
Необмежене підвищення напруги приводить
при
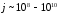 A/см2
до електричного пробою вакуумного
проміжку і руйнування емітера, якому
передує інтенсивна короткочасна вибухова
емісія електронів.
A/см2
до електричного пробою вакуумного
проміжку і руйнування емітера, якому
передує інтенсивна короткочасна вибухова
емісія електронів.
Якщо на поверхні металу є адсорбовані органічні молекули (або їхні комплекси), то для електронів вони відіграють роль хвилеводів відповідних хвиль де Бройля. При цьому спостерігаються типові для хвилеводів розподілу електронної щільності по перетині хвилеводу. Енергетичні спектри електронів у цьому випадку відрізняються аномаліями.
Відбір
струму при низьких температурах приводить
до нагрівання емітера, тому що електрони,
які емітують, забирають енергію в
середньому меншу, ніж енергія Фермі,
тоді як електрони, що входять у метал,
мають саме цю енергію (ефект Ноттингема).
Зі зростанням температури
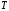 ,
нагрівання змінюється охолодженням
(інверсія ефекту Ноттингема) при досягнені
температури, що відповідає симетричному
(щодо енергії Фермі) розподілу емітованих
електронів по повних енергіях. При
великих струмах, коли емітер розігрівається,
інверсія ефекту Ноттингема частково
перешкоджає лавинному саморозігріву
і стабілізує струм тунельної емісії.
,
нагрівання змінюється охолодженням
(інверсія ефекту Ноттингема) при досягнені
температури, що відповідає симетричному
(щодо енергії Фермі) розподілу емітованих
електронів по повних енергіях. При
великих струмах, коли емітер розігрівається,
інверсія ефекту Ноттингема частково
перешкоджає лавинному саморозігріву
і стабілізує струм тунельної емісії.
Автоелектронні
емітери виготовляють у вигляді поверхонь
із великою кривизною (вістря, леза,
шорсткуваті краї фольги, напилені
мікракатоди і т.п.). У випадку, наприклад,
вістря з радіусом закруглення 0,1–1 мкм
напруги порядку 1–10 кВ звичайно буває
досить для створення біля поверхні
вістря поля
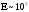 B/см.
Для відбору великих струмів та зменшення
теплового навантаження на мікракатоди
застосовуються багатовістрійні емітери.
B/см.
Для відбору великих струмів та зменшення
теплового навантаження на мікракатоди
застосовуються багатовістрійні емітери.
Відношення
загальної кількості вторинних електронів
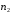 до кількості первинних електронів
до кількості первинних електронів
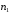 називають коефіцієнтом вторинної
електронної емісії:
називають коефіцієнтом вторинної
електронної емісії:
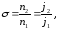 (1.8)
(1.8)
де
 — струм, утворений вторинними електронами,
— струм, утворений вторинними електронами,
 —
струм первинних електронів.
—
струм первинних електронів.
Кількісно
вторинна електронна емісія крім
коефіцієнта вторинної емісії
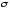 характеризується коефіцієнтами пружного
характеризується коефіцієнтами пружного
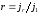 і непружнього
і непружнього
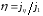 відбиття електронів, а також коефіцієнтом
емісії безпосередньо вторинних електронів
відбиття електронів, а також коефіцієнтом
емісії безпосередньо вторинних електронів
 (
(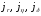 — струми, що відповідають пружно
відбитим, непружньо відбитим і істинно
вторинним електронам,
— струми, що відповідають пружно
відбитим, непружньо відбитим і істинно
вторинним електронам,
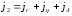 ).
).
Закон збереження енергії при фотоефекті виражається співвідношенням А. Эйнштейна:
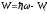 ,
,
де
 – кінетична енергія фотоелектрона,
– кінетична енергія фотоелектрона,
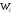 – енергія іонізації атома або робота
виходу електрона з тіла,
– енергія іонізації атома або робота
виходу електрона з тіла,
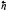 – постійна Планка,
– постійна Планка,
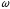 – частота випромінювання. При
– частота випромінювання. При
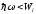 фотоефект неможливий.
фотоефект неможливий.
Якщо
середній вільний пробіг електронів
дорівнює
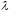 і відстань від катода до анода дорівнює
і відстань від катода до анода дорівнює
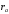 ,
то відношення числа електронів, що
проходять ця відстань без зіткнення з
газовими частками, до всього числа
електронів, що рухаються, визначається
формулою
,
то відношення числа електронів, що
проходять ця відстань без зіткнення з
газовими частками, до всього числа
електронів, що рухаються, визначається
формулою
 . (1.9)
. (1.9)
Таким чином питома потужність розжарення буде дорівнює
 .
.
Ефективність катода. Ефективністю катода називається відношення струму емісії катода до потужності, затрачуваної на його нагрівання
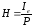 . (1.10)
. (1.10)
Ефективність показує, яку емісію можна одержати від катода на кожний Ватт потужності, затрачуваної на нагрівання катоду. Ця характеристика катода одночасно характеризує емісійні властивості катода і визначає потужність, що витрачається на розжарення. Для кожного матеріалу ефективність залежить тільки від температури, збільшуючись за експонентним законом при підвищенні температури
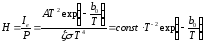 . (1.11)
. (1.11)
Із зазначеної залежності слідує, що використання катода при більше високих робочих температурах вигідно, тому що при цьому струм емісії катода збільшується, а відносна витрата потужності зменшується. Однак при високих робочих температурах значно зменшується довговічність катода.
Залежність кількості фотоелектронів, що виходять із фотокатода, тобто фотоемісійного струму jfe від величини світлового потоку Ф (від кількості квантів) при відповідній частоті v світлового потоку визначається законом Столетова Г.О.
jfe =() (1.12)
де коефіцієнт пропорційності () називається спектральною віддачею фотокатода.
Ia(екв.діода)=Iк(тріода)=Ia+Ic
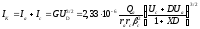
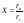
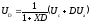
діючий потенціал,
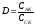
проникність тріода
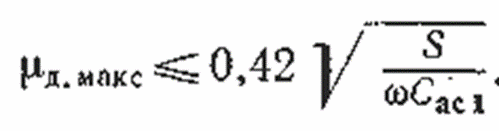
Формула Сифорова В.І., яка визначає максимальний динамічний коефіцієнт посилення каскаду
високих значеннях ККД схеми .
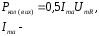
змінна складова анодного струму
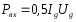
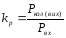
коефіцієнт посилення по потужності
Класифікація ламп по потужності розсіювання на аноді Ра .
Ра 25 Вт – малопотужні лампи. Працюють при Ua500В, за конструкцією подібні до приймально-підсилювальних ламп.
25 Вт Ра 1 кВт – лампи середньої потужності. 70% енергії джерела живлення перетворюється в коливну, решта -- на розігрів аноду. Працюють при Ua 20 кВ, застосовується примусове охолодження електродів (повітряне, водяне, вапатронне).
Ра 1 кВт – великої потужності (до 500 кВт). Виконуються, як правило, розбірними з постійною відкачкою газів, або напів-розбірними, застосовується примусове охолодження електродів (водяне, вапатронне).
Циклотронна частота обертання електронів визначається як
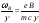
(1.1)
Коефіцієнт посилення визначається відношенням вихідної потужності Рвих до вхідної Рвх. Зазвичай цю величину визначають в децибелах:
Ку(р) = 10 lg(Рвих/Рвх). (1.1)
Ширина смуги пропускання ∆f визначається добротністю резонаторів для резонансних підсилювачів і смугою пропускання систем уповільнення хвилі, узгодженої із зовнішніми лініями передачі, для нерезонансних підсилювачів. Зазвичай ширина смуги пропускання вимірюється по рівню половинного значення вихідної потужності від максимального значення в смузі пропускання. Вона може бути вказана також у відсотках, тобто
∆f /fсер·100%
де fсер – середня частота смуги пропускання.
Коефіцієнт корисної дії визначається як відношення вихідної потужності до сумарної споживаної потужності Р0 (включаючи потужність напруження катода):
= Рвих/Р0. (1.2)
Часто використовується також поняття електронного ККД е, який дорівнює відношенню потужності, що віддається електронним пучком полю НВЧ, до потужності джерела живлення приладу.
Коефіцієнт шуму показує, в скільки разів відношення потужностей сигналу і шуму на виході підсилювача менше цього відношення на вході:
Кш = (Рш/Рш.вх)/(Рвих/Рш.вих). (1.3)
Для характеристики шумів використовують також поняття шумової температури Тш:
Кш = 1 + Тш/290 , Тш = 290(Кш - 1). (1.4)
Діапазон налаштування генератора характеризується коефіцієнтом перекриття
δп = fmax/fmin, (1.5)
де fmax і fmin – максимальна і мінімальна частоти, що генеруються.
Для автогенераторів НВЧ важливими э характеристики частоти і амплітуди коливань. Нестабільні коливання можна представити як коливання з амплітудою, що частотно змінюється:
u(t) = Uсер[1 + α(t)]cos[ωсерt + (t)dt], (1.6)
де α(t) і (t)– відносні флуктуації амплітуди і частоти, а Uсер і ωсер – середні значення амплітуди і частоти.
Як основні параметри, що характеризують шумові властивості автогенераторів, приймають спектральну щільність флуктуації амплітуди Sα (F) і частоти S (F), визначувані наближеними виразами:
Sα(F) ≈ [α2 (t)сер]∆F /∆F; S (F) ≈ [ 2(t)сер] ∆F /∆F, (1.7)
де [α2(t)сер]∆F і [ 2(t)сер]∆F – середні квадрати відносної флуктуації амплітуди і частоти, зміряні в смузі частот ∆F, F – відстань між бічною частотою модуляції і середньою частотою. Зазвичай F приймають рівною 1 кГц або 1 Гц.
Довговічність роботи приладів визначається в годинах.
Для того, щоб клістрон зміг генерувати незгасаючі НВЧ - коливання, згустки електронів, при зворотному русі, повинні проходити через резонатор в гальмівну фазу високочастотного поля. Цьому режиму відповідають оптимальний час прольоту tопт електронів в просторі групування і оптимальний кут прольоту:

опт
= tопт
= 3/2
(2)
опт
= tопт
= 3/2
(2)
Зміна кута прольоту приводить до зменшення часу ефективної взаємодії електронів, що повертаються зі НВЧ- полем резонатора і, як наслідок, зменшення амплітуди коливань і, нарешті, зриву генерації. Природно, що зміна кута прольоту на 2 знову відновлює оптимальну умову генерації. Таким чином, оптимальний кут прольоту
опт = tопт = 3/2 + 2 n (1.9)
де п =1, 2, 3...—ціле число, що визначає номер зони генерації.
Кут прольоту міняється регулюванням напруги Uвідб на відбивачі.
Коефіцієнт посилення ЛБХ залежить від вхідної потужності, частоти сигналу, режимів живлення, навантаження, а також інших факторів. Коефіцієнт посилення (у децибелах) в лінійному режимі роботи ЛБХ визначається рівнянням
![]() (1.10)
(1.10)
де
![]() параметр посилення; I0
— струм електронного пучка; U0
—
прискорювальний
потенціал; Rcв—
опір
зв'язку (величина, що визначає ефективність
зв'язку електронного пучка зі НВЧ - полем
уповільнюючої системи); lе=l
/ зам
— електрична
довжина уповільнюючої системи; l
— геометрична
довжина уповільнюючої системи; n
—
загасання
локального поглинача.
параметр посилення; I0
— струм електронного пучка; U0
—
прискорювальний
потенціал; Rcв—
опір
зв'язку (величина, що визначає ефективність
зв'язку електронного пучка зі НВЧ - полем
уповільнюючої системи); lе=l
/ зам
— електрична
довжина уповільнюючої системи; l
— геометрична
довжина уповільнюючої системи; n
—
загасання
локального поглинача.
Зміна фази вихідної напруги при зміні прискорюючої напруги Uo приблизно виражається формулою
= -105 lе (Uo /Uo ).
Для кращого розуміння роботи ЛЗХ у якості генератора НВЧ діапазону, потрібно проаналізувати фазову умову виконання позитивного зворотного зв‘язку ЛБХ, яка визначає можливість самозбудження в системі:
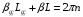 ,
,
де n=0,1,2,3…; Lзз, L – довжини системи зворотного зв‘язку та уповільнюючої системи відповідно; βзз, β – сталі розповсюдження хвиль в лінії зворотного зв‘язку та в уповільнюючій системі відповідно.
А для генерації в широкому інтервалі частот ω повинна виконуватись умова постійного значення фази хвилі в системі, при зміні частоти, або значення 0 похідної:
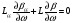 .
.
За
визначенням групової швидкості
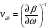 маємо:
маємо:
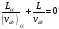 .
(1.11)
.
(1.11)
Діапазон електронної перебудови характеризується коефіцієнтом перекриття діапазону
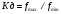
де fmах і fmin — максимальна і мінімальна граничні частоти діапазону перебудови.
Коефіцієнт перебудови ЛЗХ з коаксіальними виводами енергії Кд=2, а з хвилеводними виводами Кд ~1,5—1,6.
Ці співвідношення критичних значень прискорювального потенціалу та магнітного поля визначаються квадратним рівнянням
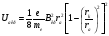 ,
,
Умовою резонансу анодного блоку магнетрона так само, як і звичайного кільцевого резонатора, є ціле число довжин хвилі, що укладаються по колу кільця-структури. Якщо позначити довжину хвилі в уповільнюючій системі упов, то умовою резонансу анодного блоку магнетрона буде
2 ra = n упов (1.13)
де ra — внутрішній радіус анодного блоку магнетрона; N — число резонаторів; п = 0, 1, 2, 3 ...
Цю ж умову можна виразити через різницю фаз коливань ( у будь-яких двох сусідніх резонаторах:
N = 2 πn (1.14)
З (1.14) видно, що різниця фаз коливань в резонаторах може набувати тільки дискретних значень: =2 n / N.
Види коливань анодного блока визначаються номером або величиною фазового зсуву .
Умова
випромінювання для швидких хвиль, що
виникають при дифракції власного поля
електронів пучка на періодичній
структурі, має вид:
де λ – довжина хвилі випромінювання, l – період структури, m = 1, 2, 3 – номер гармоніки швидких хвиль, с–швидкість світла, φ – кут дифракційного випромінювання (рис. 18а).
Для малих кутів дифракційного випромінювання (φ ≈ 0 и φ ≈ π), що генеруються пучком з попередньої модуляцією по щільності на частоті ωmod = 2πc/λ, швидкість пучка повинна складати
![]()
Так як кутовий спектр плоских хвиль, що утворюють гаусівське розподілення власного коливання відкритого резонатора, сконцентрований поблизу вісі резонатора, то для ефективної живлення резонансного коливання в ГДВ кут дифракційного випромінювання електронного пучка повинен складати φ ≈π/2.
При
цьому швидкість електронного пучка
повинна задовольняти наступному
співвідношенню:
