Практична робота №2

Тема: Тестування методом «Білого ящика».

Мета: отримати практичні навички виконання методів аналізу коду: визначення цикломатичної складності потокового графу, побудувати множини лінійних шляхів.

1 Теоретичний розділ.

1.1 Визначення потокового графа.

Для представлення програми використовується потоковий граф. Особливості потокового графа:

1. Граф будується відображенням структури програми, що управляє. При відображенні структури закриваючі|зачиняти| дужки умовних операторів і операторів циклів (end| if|; end| loop|) розглядаються|розглядують| як окремі (фіктивні) оператори.

2. 2. Вузли (вершини) потокового графа відповідають лінійним ділянкам програми, включають один або декілька операторів програми.

3. 3. Дуги потокового графа відображують|відображають| потік управління в програмі (передачі управління між операторами). Дуга — це орієнтоване ребро.

4. 4. Розрізняють операторні і предикативні вузли. З|із| операторного вузла виходить одна дуга, а з|із| предикативного — дві дуги.

5. Предикативні вузли відповідають простим умовам в програмі. Складена|складова| умова програми відображується|відображає| в декілька предикативних вузлів. Складеним|складовим| називають умову, в якій використовується одна або декілька булевих операцій (OR|, AND|).

6. Замкнуті області, утворені дугами і вузлами, називають регіонами.

7. Що оточує граф є середовище як додатковий регіон.

Наприклад, фрагмент програми

if| а OR| b |

then| x |

else| в|у|

end| if|;

замість прямого відображення в потоковий граф вигляду|виду|, показаного на Рисунку 1., відображується|відображає| в перетворений потоковий граф (рис. 2).

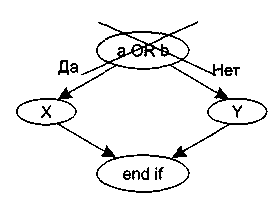
Рисунок 1. Пряме відображення в потоковий граф

Рисунок 2. Перетворений потоковий граф Наприклад, показаний тут граф має три регіони — Rl|, R2|, R3|.

Приклад 1. Розглянемо процедуру стискування:

1. виконувати доки|поки| немає EOF|

2. читати запис;

3. якщо запис пустий;|

4. то видалити|віддаляти| запис;|

5. інакше якщо поле а >= поля b

6. |то видалити|віддаляти| b;

7. інакше видалити|віддаляти| а;

7а кінець якщо; 7а кінець якщо; 7b кінець виконувати; 8. кінець стискування|стиснення|;

Рисунок 3. Перетворений потоковий граф процедури стискування

Цей потоковий граф має чотири регіони.

1.2 Порядок визначення цикломатичної складності.

Цикломатична складність - метрика ПЗ, яка забезпечує кількісну оцінку логічної складності програми. У способі тестування базового шляху|колії| цикломатична складність визначає:

• кількість незалежних шляхів|колій| в базовій множини програми;

• верхню оцінку кількості тестів, яка гарантує однократне|одноразове| виконання всіх операторів.

Незалежним називається будь-який шлях|колія|, який вводить|запроваджує| нового оператора обробки або нову умову. В термінах потокового графа незалежний шлях|колія| повинен містити|утримувати| дугу, що не входить в раніше відомі шляхи|колії|.

Шлях|колія| починається|зачинає| в початковому вузлі, а закінчується в кінцевому|скінченному| вузлі графа. Незалежні шляхи|колії| формуються в порядку|гаразд| від найкоротшого до найдовшого.

Перерахуємо незалежні шляхи|колії| для потокового графа з|із| прикладу 1|зразка|, що перед цим розглядали: |

Шлях 1: 1-8.

Шлях 2: 1-2-3-7а-7b-1-8.

Шлях 3: 1-2-4-5-7а-7b-1-8.

Шлях |колія| 4: 1-2-4-6-7а-7b-1-8.

Відмітимо|помітимо|, що кожна нова дорога|колія| включає нову дугу.

Всі незалежні шляхи|колії| графа утворюють базову множину|множину|.

Властивості базової множини: |

1) тести, що забезпечують його перевірку, гарантують:

• однократне|одноразове| виконання кожного оператора;

• виконання кожної умови по True-гілки| і по False-гілки|;

2) потужність базової множини|множини| дорівнює цикломатичної| складності потокового графа.

Значення 2-ої властивості важко переоцінити - воно дає апріорну оцінку кількості незалежних шляхфі|колій|, яка має сенс шукати в графі.

Цикломатична складність обчислюється|вичисляє| одним з трьох способів: |

1) цикломатична| складність дорівнює кількості регіонів потокового графа;

2) цикломатична| складність визначається по формулі |

V(G)=E-N+2, де Е - кількість дуг, N - кількість вузлів потокового графа;

3) цикломатична складність формується по формулі V(G)=p+ 1, де р - кількість предикативних вузлів в потоковому графові G.

Обчислимо|вичислятимемо| цикломатичну| складність графа з|із| прикладу 1|зразка|, який розглядали, кожним з трьох способів: |

1) потоковий граф має 4 регіони;

2) V(G) = 11 дуг - 9 вузлів + 2 = 4;

3) V(G) = 3 предикативних вузла +1=4.

Таким чином, цикломатическая| складність потокового графа з|із| прикладу|зразка| 1 рівна чотирьом.