4 Курс / Тестування / 04

Тема: Оцінка Покриття Програми й Проекту

Мета: дати поняття протестованості програмного продукту та навчити визначати ступінь опротестованості на основі КГП пласкої моделі та КГП ієрархічної моделі

1. Які вимоги можна сформулювати до ідеального критерію?

2. Дайте характеристику достатності критерію.

3. Дайте характеристику повноти критерію.

4. Дайте характеристику надійності критерію.

5. Які класи критеріїв можна виділити?

6. Охарактеризуйте Структурні критерії.

7. Охарактеризуйте Функціональні критерії.

8. Охарактеризуйте Критерії стохастичного тестування.

9. Охарактеризуйте Мутаційні критерії.

10. Що таке «білий ящик» в теорії тестування?

11. Що таке структурний критерій тестування команд?

12. Що таке структурний критерій тестування гілок?

13. Що таке структурний критерій тестування шляхів?

14. Що таке «чорний ящик» в теорії тестування?

15. Охарактеризуйте функціональний критерій Тестування пунктів специфікації

16. Охарактеризуйте функціональний критерій Тестування класів вхідних даних

17. Охарактеризуйте функціональний критерій Тестування правил

18. Тестування класів вихідних даних

19. Охарактеризуйте функціональний критерій Тестування функцій

20. Охарактеризуйте функціональний критерій Комбіновані критерії для програм і специфікацій

21. Дайте визначення стохастичних критеріїв.

22. Що таке Детермінований контроль тестування?

23. Що таке Стохастичний контроль тестування?

24. Які існують критерії стохастичного тестування?

25. Опишіть метод мутаційних критеріїв.

26. Що таке мутація?

27. Що таке програма-мутант?

ПЛАН

1 Оцінка опротестованості програмного продукту

2 Методика інтегральної оцінки протестованості

1 Оцінка опротестованості програмного продукту

Тестування програми Р за деяким критерієм С означає покриття множини компонентів програми P М = {m1...mk} по елементах або по зв'язках.

T = {t1...tn} - кортеж ненадлишкових тестів ti.

Тест ti ненадлишковий, якщо існує покритий їм компонент mi з M (P, C), (множини М по компонентам програми Р за критерієм С) не покритий жодним з попередніх тестів t1...ti-1. Кожному ti відповідає ненадлишковий шлях pi - послідовність вершин від входу до виходу.

V (P, C) - складність тестування Р за критерієм С - виміряється максимальним числом ненадлишкових тестів, що покривають всі елементи множини M (P, C)

DV (P, C, Т) - залишкова складність тестування Р за критерієм С - виміряється максимальним числом ненадлишкових тестів, що покривають елементи множини M (P, C), що залишилися непокритими, після прогону набору тестів Т. Величина DV строго й монотонно убуває від V до 0.

TV (P, C, Т) = (V - DV) / V - оцінка ступеня тестованості Р за критерієм С.

Критерій закінчення тестування TV (P, C, Т) >= L, де (0 <= L <= 1). L - рівень протестованості, заданий у вимогах до програмного продукту.

Рис. 4.1. Метрика протестованості додатка

Розглянемо дві моделі програмного забезпечення, використані при оцінці протестованості.

Для оцінки ступеня протестованості часто використається КГП - керуючий граф програми. КГП багатокомпонентного об'єкта G (Рис. 4.2, Приклад 4.4), що містить у собі два компоненти G1 й G2, для яких КГП розкриті.

Рис. 4.2. Плоска модель КГП компонента G

У результаті КГП компонента G має такий вигляд, ніби компоненти G1 й G2 у його структурі спеціально не виділялися, а КГП компонентів G1 й G2 вставлені в КГП G. Для тестування компонента G відповідно до критерію шляхів буде потрібно прогнати тестовий набір, що покриває наступний набір трас графа G (Приклад 4.1):

P1(G) = 1-2-3-4-5-6-7-10;

P2(G) = 1-2-3-4-6-7-10;

P3(G) = 1-2-11-16-18-14-15-7-10;

P4(G) = 1-2-11-16-17-14-15-7-10;

P5(G) = 1-2-11-16-12-13-14-15-7-10;

P6(G) = 1-2-19-20-23-22-7-10;

P7(G) = 1-2-19-20-21-22-7-10;

4.1. Набір трас, необхідних для покриття плоскої моделі КГП компонента G

Рис. 4.3. Ієрархічна модель КГП компонента G

КГП компонента G, представлений у вигляді ієрархічної моделі, наведений на Рис. 4.3, Приклад 4.5. В ієрархічному КГП G компоненти, що входять до його складу, представлені посиланнями на свої КГП G1 й G2 (Рис. 4.4, Приклад 4.5)

Рис. 4.4. Ієрархічна модель: КГП компонент G1 й G2

Для вичерпного тестування ієрархічної моделі компонента G відповідно до критерію шляхів потрібно прогнати наступний набір трас (Приклад 4.2):

P1(G) = 1-2-3-4-5-6-7-10;

P2(G) = 1-2-3-4-6-7-10;

P3(G) = 1-2-8-7-10;

P4(G) = 1-2-9-7-10.

4.2. Набір трас, необхідних для покриття ієрархічної моделі КГП компонента G

Наведений набір трас достатній за умови, що компоненти G1 й G2 у свою чергу вичерпно протестовані. Щоб забезпечити виконання цієї умови відповідно до критерію шляхів, треба прогнати всі траси Приклад 4.3.

P11(G1)=11-16-12-13-14-15;

P12(G1)=11-16-17-14-15;

P13(G1)=19-20-23-22;

P21(G2)=19-20-21-22;

P22(G2)=11-16-18-14-15.

4.3. Набір трас ієрархічної моделі КГП, необхідних для покриття КГП компонентів G1 й G2

Оцінка ступеня протестованості плоскої моделі визначається частку прогнаних трас із набору необхідних для покриття відповідно до критерію С.

(1) ,

де PTi(G) - тестовий шлях ( ti ) у графі G плоскої моделі. Дорівнює 1, якщо він протестований (прогнаний), або 0, якщо ні.

Наприклад, якщо в КГП (Приклад 4.1) тести t6 й t7, яким відповідають траси P6 й P8, не прогнані, то відповідно до співвідношення (1) для TV (G, С) ступінь протестованості складе 0.71.

Оцінка протестованості ієрархічної моделі визначається на основі обліку оцінок протестованості компонентів. Якщо траса деякого тесту tj КГП G включає вузли, що представляють компоненти Gj1,..Gjm, оцінка TV ступеня протестованості яких відома, то оцінка протестованості PTi(G) при реалізації цієї траси визначається не одиницею, а мінімальною з оцінок TV для компонентів.

Інтегральна оцінка визначається співвідношенням (2):

де PTi(G) - тестовий шлях ( ti ) у графі G рівний 1, якщо його протестовано, або 0, якщо ні. У шлях PTi графа G може входити j вузлів модулів Gij зі своїм ступенем протестованості TV(Gij,С) з яких ми беремо мінімальне значення, що дає гіршу оцінку ступеня протестованості шляху.

Нехай є наступне завдання:

Знайти значення параметра А, в залежності від Х, що може приймати лише три значення – 1, 2 або 3. у випадку, коли А знайти не можливо, прирівняти параметр -1.

Х = 1:

Х = 2: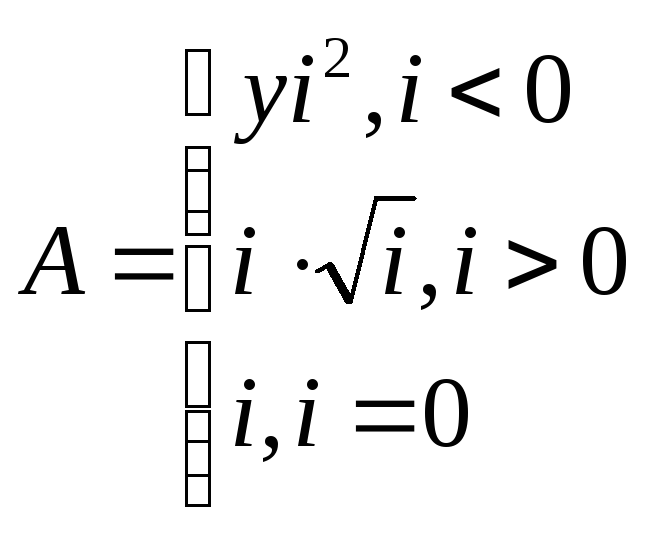

Х = 3:

#include <stdio.h>

#include <math.h>

#include <conio.h>

#include <stdlib.h >

void main()

{

int X;

int b, y,i;

float A;

puts ("input X");

scanf ("%i", &X);

puts ("input y");

scanf ("%i", &y);

switch (X){

case 1: {

puts ("input b");

scanf ("%i", &b);

if (X*y*y - b*X > 0)

A = b*y - (2*X*X - 4) / (X*y*y - b*x);

else

A = -1:

} break;

case 2: {

puts ("input i");

scanf ("%i", &i);

if (i<0) A = y*i*i;

else

if (i>0) A = i*sqrt(i);

else

A = i;

} break;

case 3:

if (X*y*y - y>0)

A = sqrt(X*y*y - y);

else

A = -1;

}break;

}

printf ("A = %f\n", A);

getch ();

}

// Приклад плоскої моделі проекту

void G()

{

int TerminalStatus=0, CommandStatus=0;

int IsPresent=1, CommandFound=1;

1 Init();

2 switch (TerminalStatus)

{

case 11 :

11 AddCommand();

16 switch (CommandStatus)

{

case 12 :

12 GetMessage();

13 ClearQueue(); break;

case 17 :

17 ClearQueue(); break;

case 18 :

18 DumpQueue(); break;

}

14 ProcessCommand();

15 Commit(); break;

case 3 :

3 AskTerminal();

4 if (IsPresent)

{

5 Connect();

}

6 RebuildQueue(); break;

case 19 :

19 SearchValidCommand();

20 if (CommandFound)

{

21 AnalyzeCommand();

}

else

{

23 LogError();

}

22 MoveNextCommand(); break;

}

7 LogResults();

10 DisposeAll();

}

Приклад 4.1. Приклад програми для плоскої моделі (Рис. 4.2)

// Приклад ієрархічної моделі проекту

void G1()

{

int CommandStatus=0;

AddCommand();

switch (CommandStatus)

{

case 12 :

GetMessage();

ClearQueue();

break;

case 17 :

ClearQueue();

break;

case 18 :

DumpQueue();

break;

}

ProcessCommand();

Commit();

}

void G2()

{

int CommandFound=1;

SearchValidCommand();

if (CommandFound)

{

AnalyzeCommand();

}

else

{

LogError();

}

MoveNextCommand();

}

void G()

{

int TerminalStatus=0;

int IsPresent=1;

1 Init();

2 switch (TerminalStatus)

{

case 11 :

8 G1(); break;

case 3 :

3 AskTerminal();

4 if (IsPresent)

{

5 Connect();

}

6 RebuildQueue(); break;

case 19 :

9 G2(); break;

}

7 LogResults();

10 DisposeAll();

}

Приклад 4.5.1. Приклад програми для ієрархічної моделі (Рис. 4.3)

2 Методика інтегральної оцінки протестованості

1. Вибір критерію С и припустимої оцінки протестованості програмного проекту - L

2. Побудова древа класів проекту й побудова КГП для кожного модуля

3. Модульне тестування й оцінка TV на модульному рівні

4. Побудова КГП, що інтегрує модулі в єдину ієрархічну ( класову ) модель проекту

5. Вибір тестових шляхів для проведення інтеграційного або системного тестування

6. Генерація тестів, що покривають тестові шляхи кроку 5

7. Інтегральна оцінка протестованості проекту з урахуванням оцінок протестованості модулів-компонентів

Повторення кроків 5-7 до досягнення заданого рівня протестованості L

Контрольні питання

1. Як можна розуміти тестування певної програми за деяким критерієм?

2. Який тест з множини всіх тестів є не надлишковим?

3. Що таке ненадлишковий шлях?

4. Що таке складність тестування за критерієм? Як і чим вона вимірюється?

5. Що таке залишкова складність тестування? Як і чим вона вимірюється?

6. Що таке критерій закінчення тестування?

7. Які значення він може приймати?

8. Що таке плоска модель КГП компонента? Як вона будується?

9. Що таке ієрархічна модель КГП компонента? Чим вона відрізняється від пласкої?

10. Як і навіщо можна визначити ступінь опротестованості моделі (програми)?

11. В чому полягає методика інтегральної оцінки опротестованості?

12. Опишіть та поясніть кроки даної методики.

8