Добавил:

masterdos Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сумский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Практична робота №4

.doc

Скачиваний:

Добавлен:

30.05.2020

Размер:

6.18 Mб

Скачать

☆

Практична робота № 4

Тема: Тестування методом «чорного ящика». Способи діаграм причин - наслідків.

Мета: Освоїти на практиці метод діаграм причин – наслідків. Сформувати тестові набори та побудувати причинно-наслідкову діаграму.

Теоретичний розділ

Діаграма причинно-наслідкових зв'язків допомагає відбити можливі причини, що впливають на якість продукту чи процесу в проекті. Така діаграма, яку також називають діаграмою Ішикави або діаграмою риб'ячого скелета, ілюструє зв'язок різних факторів з можливими проблемами або ефектами. Крім цього за діаграмою можна спрогнозувати очікуваний результат на основі внесених даних.

Призначення методу

Застосовується при розробці та безперервному вдосконаленні продукції. Діаграма Ішикави - інструмент, що забезпечує системний підхід до визначення фактичних причин виникнення проблем.

Мета методу

Вивчити, відобразити і забезпечити технологію пошуку справжніх причин розглянутої проблеми для ефективного їх вирішення.

Суть методу

Причинно-наслідковий діаграма - це ключ до вирішення виникаючих проблем.

Діаграма дозволяє в простій і доступній формі систематизувати всі потенційні причини розглянутих проблем, виділити найістотніші і провести пошук першопричини неполадки по рівням виконання.

План дій

У відповідності з відомим принципом Парето, серед безлічі потенційних причин (причинних факторів, у Ішикави) , що породжують проблеми (слідство) , лише дві – три є найбільш значущими , їх пошук і повинен бути організований. Для цього здійснюється :

збір та систематизація всіх причин, що прямо або побічно впливають на досліджувану проблему;
групування цих причин по смисловим і причинно-наслідковим блокам;
ранжування їх усередині кожного блоку;
аналіз картини, що вийшла.

Особливості методу

Причинно-наслідковий діаграма ("риб'ячий скелет")

Загальні правила побудови

Перш ніж приступати до побудови діаграми, всі учасники повинні прийти до єдиної думки щодо формулювання проблеми.

Досліджувана проблема записується з правого боку в середині чистого аркуша паперу і береться в рамку, до якої зліва підходить основна горизонтальна стрілка - "хребет" (діаграму Ішикави через зовнішній вигляду часто називають "риб'ячим скелетом").

Наносяться головні причини (причини рівня 1), що впливають на проблему, - "великі кістки". Вони беруться в рамки в рамки і з'єднуються похилими стрілками з "хребтом" .

Далі наносяться вторинні причини (причини рівня 2), які впливають на головні причини ("великі кістки"), а ті, в свою чергу, є наслідком вторинних причин . Вторинні причини записуються і розташовуються у вигляді " середніх кісток ", що примикають до "великих". Причини рівня 3, які впливають на причини рівня 2, розташовуються у вигляді "дрібних кісток", що примикають до "середніх", і т. д. (Якщо на діаграмі наведені не всі причини , то одна стрілка залишається порожньою).

При аналізі повинні виявлятися і фіксуватися усі фактори , навіть ті, які здаються незначними, оскільки мета схеми - відшукати найбільш правильний шлях і ефективний спосіб вирішення проблеми.

Причини (фактори) оцінюються і ранжуються за їх значимістю, виділяючи особливо важливі, які ймовірно мають найбільший вплив на показник якості.

У діаграму вноситься вся необхідна інформація: її назва; найменування виробу; імена учасників; дата і т. д.

Додаткова інформація:

Процес виявлення , аналізу і пояснення причин , є ключовим у структуруванні проблеми і переходу до коригувальних дій.

Задаючи при аналізі кожної причини питання "чому ?" , Можна визначити першопричину проблеми (за аналогією з виявленням головної функції кожного елемента об'єкта при функціонально - вартісному аналізі).

Спосіб поглянути на логіку в напрямку "чому?" полягає в тому, щоб розглядати цей напрям у вигляді процесу поступового розкриття всього ланцюга послідовно пов'язаних між собою причинних факторів, що роблять вплив на проблему якості.

Переваги методу

Діаграма Ішикави дозволяє:

стимулювати творче мислення ;
представити взаємозв'язок між причинами і зіставити їх відносну важливість.

Недоліки методу

Не розглядається логічна перевірка ланцюжка причин, що ведуть до першопричини, тобто відсутні правила перевірки в зворотному напрямку від першопричини до результатів .
Складна і не завжди чітко структурована діаграма не дозволяє робити правильні висновки.

Практичний розділ

Виконання роботи передбачає наступну послідовність дій:

Визначення причин (умов введення) і наслідків;
Побудова графа причинно-наслідкових зв'язків;
Створення таблиць рішень;
Побудова тестових варіантів;
Оформлення результатів тестування.

У звіт по лабораторній роботі входять:

Перелік причин і наслідків;
Граф причинно-наслідкових зв'язків;
Таблиця рішень;
Тестові варіанти;
Програмний код;
Результати тестування (відповідні скрін-шоти).

Приклад виконання роботи

Завдання:

Використовуючи операторів if/else розв’язати квадратне рівняння вигляду:

Текст програми:

#include<iostream.h>

#include<math.h>

void main()

{

double а,c,b,D,x1,x2,x,x3;

cout<<"Vvedite Chisllo с - ";

cin>>c;

cout<<"Vvedite Chisllo а - ";

cin>>a;

cout<<"Vvedite Chisllo b - ";

cin>>b;

D=a*a-4*c*b;

// if| (a=0)

// else

if (c==0)

if(a==0)

{ cout<<"Net| kornei|";}

else|

if| (b==0|)

{

cout<<"Mnogestvo| rewenii|";

}

else|

{ x=-b/a;

cout<<"\n| x="<<x|;

}

else|

if| (D<0|)

{

cout<<"\n| Net| kornei|";

}

else|

//if| (b=0|)

if| (D>0|)

{

x1=|(-a*a+sqrt(D)/2*c|);

x2=|(-a*a-sqrt(D)/2*c|);

cout<<"\n| x1=| "<<x1|;

cout<<"\n| x2=| "<<x2|;

}

else|

{

x3=-a/2*c;

cout<<"x3=| "<<x3|;

}

//cout<<"\n| D: "<<D|;

//cout<<"\n| Press| any| key| to| EXIT|";

}

Крок 1. Причинами є:

C = 0|
C > 0|
D > 0|
D = 0|
D < 0|
B = 0|, А = 0|
А ≠ 0, В ≠ 0

На основі різних комбінацій причин можна перерахувати наступні дії|:

101 - 2 кореня

102 - 1 корінь

103 - немає коріння

104 – безкінечна множина рішень

Крок 2. Розробка графа причинно-наслідкових зв'язків. Вузли причин перераховують по вертикалі зліва, а вузли наслідків – справа.

Крок 3. Генерація таблиці рішень. Причини розглядаються як умови, а следствия – як дії.

Номери стовпців			1	2	3	4	5	6
Умови (причини)	Причини	1	1	1	1	0	0	0
		2	0	0	0	1	1	1
		3	x	x	x	1	0	0
		4	x	x	x	0	1	0
		5	x	x	x	0	0	1
		6	1	0	0	x	x	x
		7	0	1	0	x	x	x
		8	0	0	1	x	x	x
	Вторинні	11	1	0	0	0	0	0
	причини	12	0	1	0	0	0	0
		13	0	0	1	0	0	0
		14	0	0	0	1	0	0
		15	0	0	0	0	1	0
		16	0	0	0	0	0	1
Дія	слідство	101	0	0	0	1	0	0
		102	0	0	1	0	1	0
		103	0	1	0	0	0	1
		104	1	0	0	0	0	0

Крок 4. Перетворення кожного стовпця таблиці в тестовий варіант. У нашому прикладі 4 тестових варіанту.

ТВ 1 (стовпець 1):

ВД|: с=0| b=0| a=0|

Очікуваний результат: Mnogestvo| rewenii|

ТВ 2 (стовпець 2):

ВД|: C=0| a=0| b=2|

Очікуваний результат: Net| kornei|

ТВ 3 (стовпець 3):

ВД|: C=0| a=| -4 b=2|

Очікуваний результат: x=| 0,5

ТВ 4 (стовпець 4):

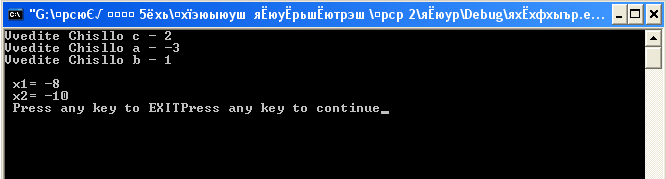
ВД|: C=2| a=| -3 b=1| (D=1|)

Очікуваний результат: x1=| -8 x2=| -10

ТВ 5 (стовпець 5):

ВД|: C=2| a=4| b=2| (D=0|)

Очікуваний результат: x=| -4

ТВ 6 (стовпець 6):

ВД|: C=8| a=-2| b=6| (D=-188|)

Очікуваний результат: Net| kornei|

ТВ 1

ТВ 2

ТВ3

ТВ 4

ТВ 5

ТВ 6

Завдання

Згідно списку академічної групи обрати завдання з таблиці. Перші два стовпчики містить фігури на площині, третій – характеристики. Завдання полягає в наступному – проаналізувати масиви координат з додатку до роботи, щодо положення точок відносно базових фігур. Крім цього треба створити програмний код, що здійснить перевірку положення точки щодо фігури. Варто враховувати, що запропоновані точки не враховують граничних умов – їх необхідно задавати самостійно. За даними розрахунків будується діаграма Ішикави.

			Діаметр більшого кола – 2 одиниці, діаметр меншого кола – одиниця. Відстань від точок –d та d до початку координат – 2 одиниці, відстань від точок –с та с до початку координат – одиниця.
			Координати точок: е (0, 6); е1 (0, 4); с (2, 0); с1 (3,0); d1 (5,0); d (6,0). Діаметр кола – 4 одиниці.
			Діаметр кола – 3 одиниці. Координати точки А (-π/2, -1), точки В (π/2, 1)
			Координати точок f(0, 4); g (0, 1); с (1,0); d (2, 0); е (3,0). Довжина сторони більшого квадрату – 4 одиниці, меншого квадрату – 2 одиниці.
			Діаметр кола – 4 одиниці. Координати центра кола А – (-1, 1); кола В – (1, -1)
			Довжина сторони більшого квадрату – 4 одиниці, меншого квадрату – 2 одиниці. Діаметр кола – 3 одиниці.
			Діаметр кола – 4 одиниці. Діаметр меншого кола – 6 одиниць, більшого – 12.
			Довжина сторони більшого квадрату – 4 одиниці, меншого квадрату – 2 одиниці. Координати точки с (0, 2.5), точки d(3, 0)
			Координати точок d(0, 1), d1 (0, 3), d2 (0, 6), с (2, 0), с1 (6, 0), с2 (10, 0), А (6, 3). Діаметр кола – 2 одиниці. Відстань від точок –d та d до початку координат – 2 одиниці, від точки с – 2,5 одиниці.
			Координати точки е (1, 0), довжина сторони шестикутника – 2 одиниці. Довжина сторони квадрату – 4 одиниці.
			Відстань до точки d до початку координат – 2 одиниці, від точки с – 3 одиниці. Довжина сторони квадрату – 4 одиниці.
			Діаметр більшого кола – 2 одиниці, діаметр меншого кола – одиниця. Діаметр кола – 2,5 одиниці.
			Довжина сторони квадрату – 4 одиниці. Координати точки А (-π/2, 1), точки В (π/2, 2)
			Координати точки е (1, 0), довжина сторони шестикутника – 2 одиниці. Відстань від точок –d та d до початку координат – 2 одиниці, від точки -с – 2,5 одиниці.
			Координати центра кола А – (-1, 1); кола В – (1, -1) Відстань до точки d до початку координат – 2 одиниці, від точки с – 3 одиниці.
			Координати точок d(0, 1), d1 (0, 3), d2 (0, 6), с (2, 0), с1 (6, 0), с2 (10, 0), А (6, 3). Діаметр кола – 2 одиниці. Радіус кола – 2,5 одиниці.