1.4.Алгебра множеств

Множество всех подмножеств универсального множества U вместе с операциями над множествами образуют так называемую алгебру подмножеств множества U или алгебру множеств.

Основными составляющими алгебры множеств являются операции над множествами и свойства этих операций, которые формулируются в виде основных тождеств или законов алгебры множеств.

1.4.1Операции над множествами

Над множествами определены следующие операции: объединение, пересечение, разность (относительное дополнение), симметрическая разность и дополнение (абсолютное).

Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1.3 а):

AB = {x | x A или xB}.

Операцию объединения можно распространить на произвольное, в том числе и бесконечное количество множеств, например, М=АВСD. В общем случае используется обозначение А, которое читается так: “объединение всех множеств А, принадлежащих совокупности S ”.

Если же все множества совокупности индексированы (пронумерованы с помощью индексов), то используются другие варианты обозначений:

1. А_i, если S={A₁,A₂,…,A_k};

2. А_i, если S – бесконечная совокупность пронумерованных множеств;

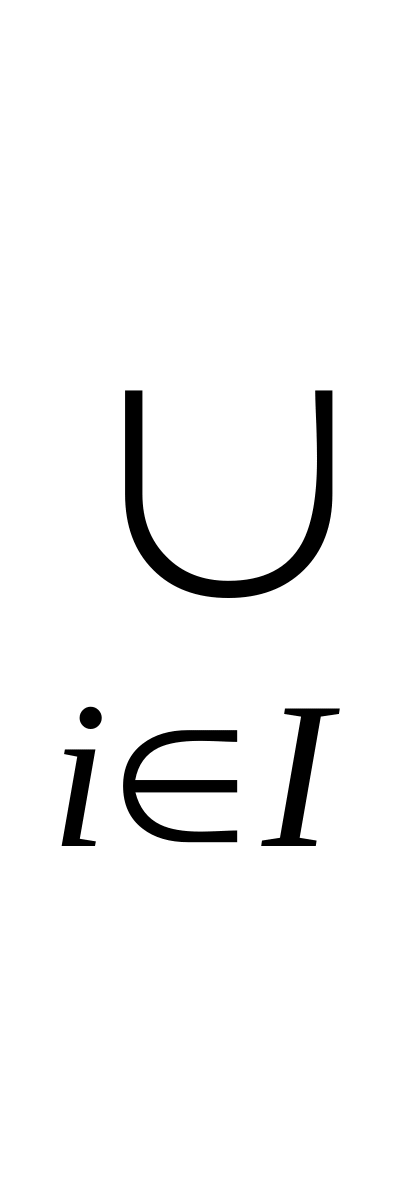3. А_i, если набор индексов множеств задан множеством I.

Пример 1.2.

А={a,b,c}, B={b,c,d}, C={c,d,e}.

AB={a,b,c,d}; AC={a,b,c,d,e}; BC={b,c,d,e}; ABC={a,b,c,d,e}.

Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 1.3 б):

AB = {x | x A и xB}.

Аналогично определяется пересечение произвольной (в том числе бесконечной) совокупности множеств. Обозначение для пересечения системы множеств аналогичны рассмотренным ранее обозначениям для объединения.

Пример 1.3. (для множеств из примера 1.2):

АВ={b,c}; AC={c}; BC={c,d}; ABC={c}.

Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 1.3 в):

A \ B = {x | x A и xB}.

Разность множеств А и В иначе называется дополнением множества А до множества В (относительным дополнением).

Пример 1.4. (для множеств из примера 1.2)

А\В={а, b, c} \ {b,c,d}={a}.

Симметрической разностью множеств А и В называется множество, состоящее из элементов, которые принадлежат либо только множеству А, либо только множеству В (рис. 1.3 г). Симметрическую разность обозначают как AΔB, A – B или A  B:

AΔB = {x | (x A и xB) или ( x В и xА)}.

Таким образом, симметрическая разность множеств A и B представляет собой объединение разностей (относительных дополнений) этих множеств: AΔB = (A \ B)  (B \ A).

Пример 1.5. (для множеств из примера 1.2)

AΔB ={a}{d}={a,d}.

Дополнением (абсолютным) множества А называется множество всех тех элементов х универсального множества U, которые не принадлежат множеству А (рис. 1.3 д). Дополнение множества А обозначается :

={x xA}=U \ A.

С учетом введенной операции дополнения, разность множеств А и В можно представить в виде: A \ B=A .

Операции над множествами используются для получения новых множеств из уже существующих. Порядок выполнения операций над множествами определяется их приоритетами в следующем порядке: ,  , , \ , Δ.