t = [0 0.3 0.8 1.1 1.6 2.3]';
y = [0.5 0.82 1.14 1.25 1.35 1.40]';
plot(t,y,'o'); grid on
В следующих разделах мы рассмотрим три способа моделирования(аппроксимации) этих данных:
·Методом полиномиальной регрессии
·Методом линейно-параметрической (linear-in-the-parameters) регрессии
·Методом множественной регрессии
Полиномиальная регрессия
Основываясь на виде графика, можно допустить, что данные могут быть аппроксимированы полиномиальной функцией второго порядка:
y = a0 + a1t + a2t2
Неизвестные коэффициенты a0 , a1 и a2 могут быть найдены методом среднеквадратической подгонки (аппроксимации), которая основана на минимизации суммы квадратов отклонений данных от модели. Мы имеем шесть уравнений относительно трех неизвестных,
представляемых следующей матрицей 6х3:
57
|
X = [ones(size(t)) |
t t.^2] |
|
X = |
1.0000 |
0 |
0 |
|
1.0000 |
0.3000 |
0.0900 |
|
1.0000 |
0.8000 |
0.6400 |
|
1.0000 |
1.1000 |
1.2100 |
|
1.0000 |
1.6000 |
2.5600 |
|
1.0000 |
2.3000 |
5.2900 |
Решение находится при помощи оператора \ :
a = X\y
a =
0.5318
0.9191 - 0.2387
Следовательно, полиномиальная модель второго порядка наших данных будет иметь вид
y = 0.5318 + 0.9191t – 0.2387 t2
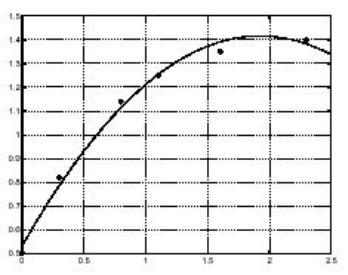
Оценим теперь значения модели на равноотстоящих точках (с шагом 0.1) и нанесем кривую на график с исходными данными.
T = (0 : 0.1 : 2.5)';
Y = [ones(size(T)) T T.^2]*a;
plot(T,Y,'-',t,y,'o'); grid on
Очевидно, полиномиальная аппроксимация оказалась не столь удачной. Здесь можно или повысить порядок аппроксимирующего полинома, или попытаться найти какую-либо другую функциональную зависимость для получения лучшей подгонки.
58
Линейно-параметрическая регрессия1
Вместо полиномиальной функции, можно было-бы попробовать так называемую линейнопараметрическую функцию. В данном случае, рассмотрим экспоненциальную функцию
y = a0 + a1℮-t + a2t℮-t
Здесь также, неизвестные коэффициенты a0 , a1 и a2 могут быть найдены методом наименьших квадратов. Составим и решим систему совместных уравнений, сформировав регрессионную матрицу X, и применив для определения коэффициентов оператор \ :
X = [ones(size(t)) exp(- t) t.*exp(- t)];
a = X\y
a =
1.3974
-0.8988
0.4097
Значит, наша модель данных имеет вид
y = 1.3974 – 0.8988℮-t + 0.4097t℮-t
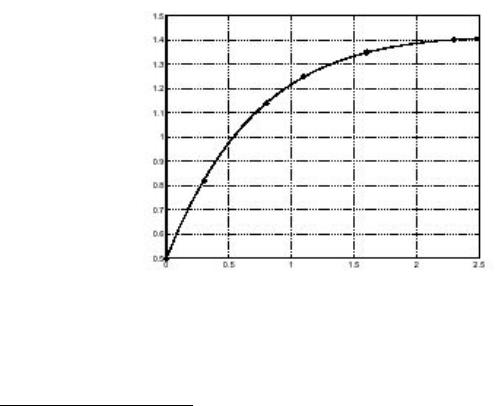
Оценим теперь, как и раньше, значения модели на равноотстоящих точках (с шагом 0.1) и нанесем эту кривую на график с исходными данными.
Как видно из данного графика, подгонка здесь намного лучше чем в случае полиномиальной функции второго порядка.
1 Данная терминология не совсем соответствует принятой в русско-язычных изданиях.
59
Множественная регрессия
Рассмотренные выше методы аппроксимации данных можно распространить и на случай более чем одной независимой переменной, за счет перехода к расширенной форме записи. Допустим, мы измерили величину y для некоторых значений двух параметровx1 и x2 и получили следующие результаты
x1 = [0.2 |
0.5 |
0.6 |
0.8 |
1.0 |
1.1]' ; |
x2 = [0.1 |
0.3 |
0.4 |
0.9 |
1.1 |
1.4]' ; |
y = [0.17 0.26 0.28 |
0.23 |
0.27 0.24]' ; |
|||
Множественную модель данных будем искать в виде
y = a0 + a1x1 + a2x2
Методы множественной регрессии решают задачу определения неизвестных коэффициентов a0 , a1 и a2 путем минимизации среднеквадратической ошибки приближения. Составим совместную систему уравнений, сформировав матрицу регрессии X и решив уравнения относительно неизвестных коэффициентов, применяя оператор \ .
X = [ones(size(x1)) x1 x2];
a = X\y
a =
0.1018
0.4844 -0.2847
Следовательно, модель дающая минимальную среднеквадратическую ошибку аппроксимации имеет вид
y = 0.1018 + 0.4844x1 – 0.2847x2
Для проверки точности подгонки найдем максимальное значение абсолютного значения отклонений экспериментальных и расчетных данных.
Y = X*a;
MaxErr = max(abs(Y - y))
MaxErr =
0.0038
Эта ошибка дает основание утверждать, что наша модель достаточно адекватно отражает результаты наблюдений.
60