
Лекция 6
.docАсиметричні криптосистеми
План
1 Концепція криптосистеми з відкритим ключем
2 Односпрямовані функції
3 Криптосистема шифрування даних RSA
4 Схема шифрування Поліга - Хеллмана
5 Алгоритм шифрування Ель Гамаля
6 Схема шифрування Рабіна
1 Концепція криптосистеми з відкритим ключем
Ефективними системами криптографічного захисту даних є асиметричні криптосистеми, які називають також криптосистемами з відкритим ключем. У таких системах для зашифрування даних використовується один ключ, а для розшифрування – інший ключ (звідси й назва – асиметричні). Перший ключ є відкритим і може бути опублікований для використання всіма користувачами системи, які зашифровують дані. Розшифрувати дані за допомогою відкритого ключа неможливо.
Для розшифрування даних одержувач зашифрованої інформації використовує другий ключ, що є таємним. Зрозуміло, таємний ключ не може бути визначений, виходячи з відкритого ключа.
Узагальнена
схема криптосистеми з відкритим ключем
показана на рисунку 1. В цій криптосистемі
застосовують два різних ключі:
![]() – відкритий ключ відправника A;
– відкритий ключ відправника A;
![]() – таємний ключ одержувача В.
– таємний ключ одержувача В.
Генератор
ключів доцільно розташовувати на стороні
одержувача B,
щоб не пересилати таємний ключ
![]() незахищеним каналом. Значення ключів
незахищеним каналом. Значення ключів
![]() і
і
![]() залежать від початкового стану генератора
ключів.
залежать від початкового стану генератора
ключів.
Розкриття
таємного ключа
![]() за значенням відомого відкритого ключа
за значенням відомого відкритого ключа
![]() повинно бути обчислювально нерозв’язаною
задачею.
повинно бути обчислювально нерозв’язаною
задачею.
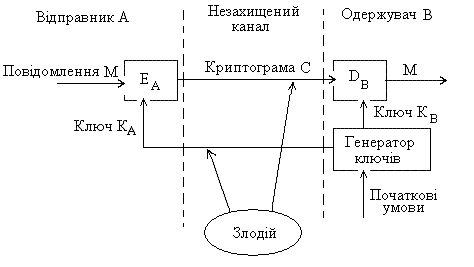
Рисунок 1 – Узагальнена схема асиметричної криптосистеми
Характерні риси асиметричних криптосистем:
-
Відкритий ключ
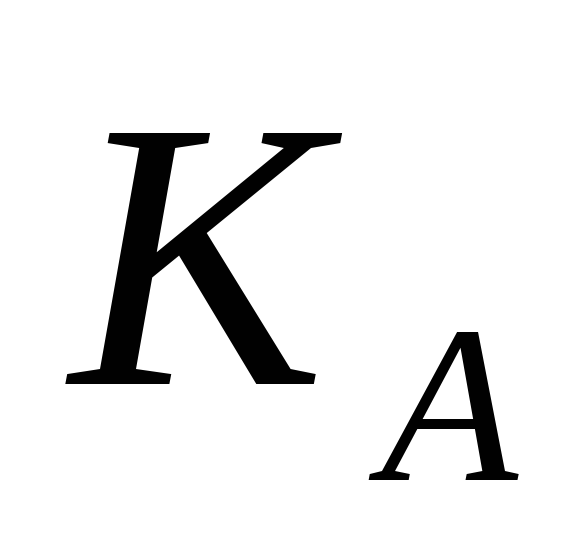 і криптограма C
можуть бути відправлені по незахищених
каналах, тобто зловмиснику відомі
значення
і криптограма C
можуть бути відправлені по незахищених
каналах, тобто зловмиснику відомі
значення
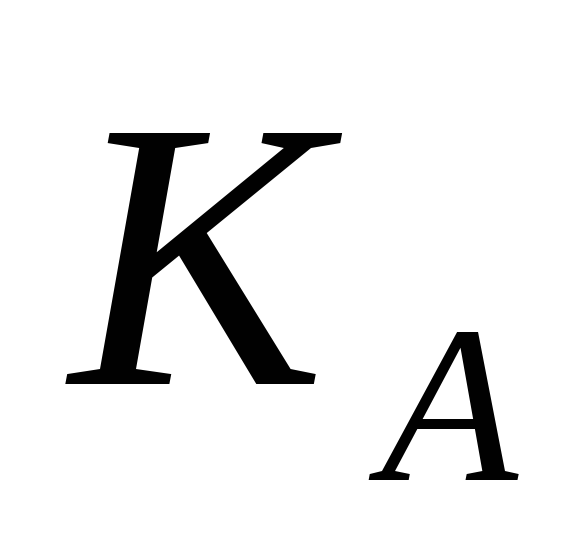 та C.
та C. -
Алгоритми шифрування (
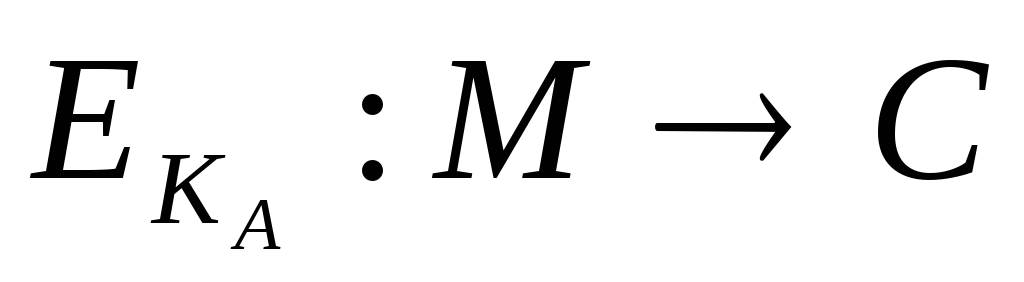 )
і розшифрування
)
і розшифрування
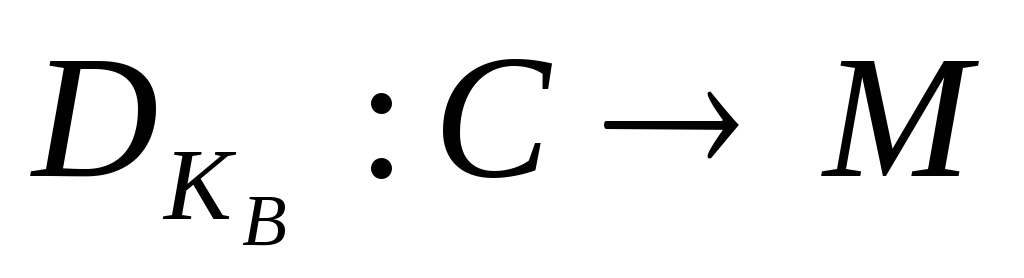 є
відкритими.
є
відкритими.
Захист
інформації в асиметричній криптосистемі
засновано на таємності ключа
![]() .
.
У.Діффі та М.Хеллман сформулювали вимоги, які забезпечують безпеку асиметричної криптосистеми:
-
Обчислення пари ключів (
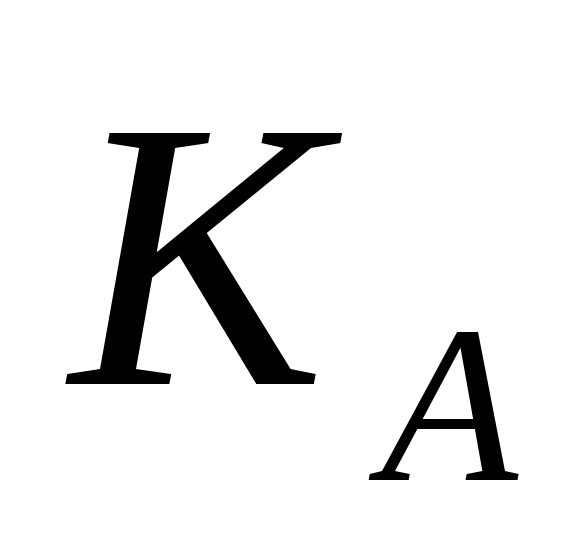 ,
, 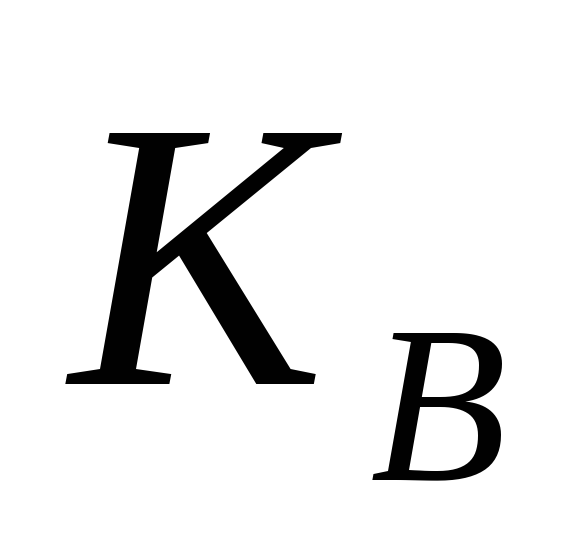 )
одержувачем B
на основі початкової умови повинно
бути простим.
)
одержувачем B
на основі початкової умови повинно
бути простим. -
Відправник A, знаючи відкритий ключ
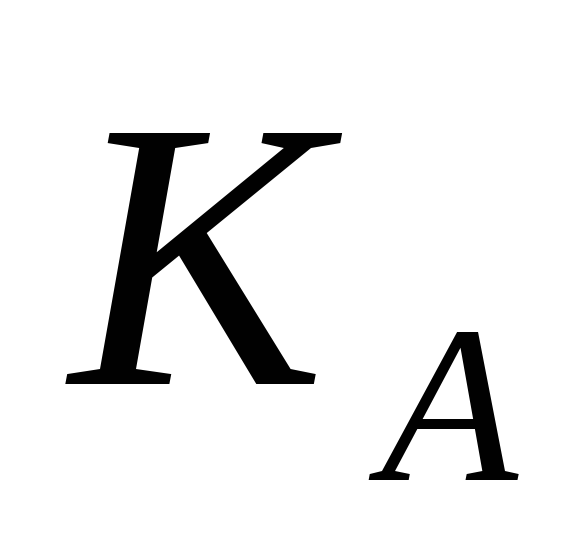 і повідомлення М,
може легко обчислити криптограму
і повідомлення М,
може легко обчислити криптограму
![]() . (4.1)
. (4.1)
3 Одержувач В,
використовуючи таємний ключ
![]() і криптограму C,
може легко відновити вихідне повідомлення
і криптограму C,
може легко відновити вихідне повідомлення
![]() . (4.2)
. (4.2)
4 Зловмисник,
знаючи відкритий ключ
![]() ,
при спробі обчислити таємний ключ
,
при спробі обчислити таємний ключ
![]() натрапляє на непереборну обчислювальну
проблему.
натрапляє на непереборну обчислювальну
проблему.
5 Зловмисник,
знаючи пари (![]() , C),
при спробі обчислити вихідне повідомлення
M
натрапляє на непереборну обчислювальну
проблему.
, C),
при спробі обчислити вихідне повідомлення
M
натрапляє на непереборну обчислювальну
проблему.
2 Односпрямовані функції
Концепція асиметричних криптографічних систем з відкритим ключем заснована на застосуванні односпрямованих функцій. Неформально односпрямовану функцію можна визначити в такий спосіб.
Нехай
Х
і Y
–
деякі довільні множини. Функція
![]() є
односпрямованою,
якщо для всіх
є
односпрямованою,
якщо для всіх
![]() можна легко обчислити функцію
можна легко обчислити функцію
![]() ,
але для більшості
,
але для більшості
![]() досить складно одержати значення
досить складно одержати значення
![]() ,
таке, що
,
таке, що
![]() (при цьому вважають, що існує принаймні
одне таке значення
(при цьому вважають, що існує принаймні
одне таке значення
![]() ).
).
Основним
критерієм віднесення функції
![]() до класу
односпрямованих функцій є відсутність
ефективних алгоритмів зворотного
перетворення
до класу
односпрямованих функцій є відсутність
ефективних алгоритмів зворотного
перетворення
![]() .
.
Як
приклад односпрямованої функції
розглянемо множення цілих чисел. Пряма
задача – обчислення добутку двох дуже
великих цілих чисел
![]() й
й
![]() ,
тобто знаходження значення
,
тобто знаходження значення
![]() (4.3)
(4.3)
є простою задачею для ЕОМ.
Зворотна
задача – розкладання на множники
великого цілого числа, тобто знаходження
дільників
![]() і
і
![]() великого цілого числа
великого цілого числа
![]() ,
є практично нерозв’язною задачею при
досить великих значеннях
,
є практично нерозв’язною задачею при
досить великих значеннях
![]() .
.
За
сучасними оцінками теорії чисел при
цілому
![]() й
й
![]() для розкладання числа
для розкладання числа
![]() буде потрібно близько 1023
операцій, тобто задача практично
нерозв’язна.
буде потрібно близько 1023
операцій, тобто задача практично
нерозв’язна.
Наступний
характерний приклад односпрямованої
функції – це модульна експонента з
фіксованими підставою й модулем. Нехай
![]() й
й
![]() –
цілі
числа, такі, що
–
цілі
числа, такі, що
![]() .
Визначимо множину
.
Визначимо множину
![]()
![]() .
.
Тоді
модульна експонента з основою
![]() за модулем N
являє собою функцію
за модулем N
являє собою функцію
![]()
![]() ,
,
де
![]() – ціле число,
– ціле число,
![]() .
.
Існують
ефективні алгоритми, що дозволяють
досить швидко обчислити значення функції
![]() .
.
Якщо
![]() ,
то, природно,
,
то, природно,
![]() .
.
Тому,
задачу обернення функції
![]() називають
задачею знаходження
дискретного логарифма
або задачею дискретного
логарифмування.
називають
задачею знаходження
дискретного логарифма
або задачею дискретного
логарифмування.
Задача дискретного логарифмування формулюється в такий спосіб.
Для
відомих цілих
![]() знайти ціле число
знайти ціле число
![]() ,
таке, що
,
таке, що
![]() .
.
Алгоритм обчислення дискретного логарифма за прийнятний час поки не знайдена, тому модульна експонента вважається односпрямованою функцією.
За
сучасними оцінками теорії чисел при
досить великих цілих числах A2664
й N2664
рішення задачі дискретного логарифмування
(знаходження показника ступеня
![]() для відомого
для відомого
![]() )
потребує близько 1026
операцій, тобто ця задача має в 103
разів більшу обчислювальну складність,
ніж задача розкладання на множники.
Різниця в оцінках складності задач
зростає при збільшенні довжини чисел.
)
потребує близько 1026
операцій, тобто ця задача має в 103
разів більшу обчислювальну складність,
ніж задача розкладання на множники.
Різниця в оцінках складності задач
зростає при збільшенні довжини чисел.
Відзначимо, що поки не вдалося довести, що не існує ефективного алгоритму обчислення дискретного логарифма за прийнятний час. Виходячи з цього, модульна експонента віднесена до односпрямованих функцій умовно, що однак не заважає з успіхом застосовувати її на практиці.
Другим важливим класом функцій, що використовуються при побудові криптосистем з відкритим ключем, є односпрямовані функції з "потаємним ходом".
Функція
![]() належить
до класу односпрямованих функцій з
"потаємним ходом" у тому випадку,
якщо вона є односпрямованою й, крім
того, можливо ефективне обчислення
зворотної функції, якщо відомо "потаємний
хід" (таємне число, рядок або інша
інформація, що асоціюється з даною
функцією).
належить
до класу односпрямованих функцій з
"потаємним ходом" у тому випадку,
якщо вона є односпрямованою й, крім
того, можливо ефективне обчислення
зворотної функції, якщо відомо "потаємний
хід" (таємне число, рядок або інша
інформація, що асоціюється з даною
функцією).
Як приклад односпрямованої функції з "потаємним ходом" можна вказати модульну експоненту з фіксованими модулем і показником ступеня, що використовується в криптосистемі RSA. Змінна основа модульної експоненти використовується для вказівки числового значення повідомлення М або криптограми С.
3 Криптосистема шифрування даних RSA
Алгоритм RSA запропонували в 1978 р. Р.Райвест (Rivest), А.Шамір (Shamir) і А.Адлеман (Adleman). Алгоритм одержав свою назву від перших букв прізвищ його авторів. Алгоритм RSA став першим повноцінним алгоритмом з відкритим ключем, що може працювати як у режимі шифрування даних, так і у режимі електронного цифрового підпису.
Надійність алгоритму ґрунтується на труднощі факторизації великих чисел і труднощі обчислення дискретних логарифмів.
У
криптосистемі RSA розглядають: відкритий
ключ
![]() ;
таємний ключ
;
таємний ключ
![]() ;
повідомлення
;
повідомлення
![]() й криптограма
й криптограма
![]() належать множині цілих чисел
належать множині цілих чисел
![]() , (4.4)
, (4.4)
де
![]() -
модуль
-
модуль
![]() .
(4.5)
.
(4.5)
Тут
![]() й
й
![]() – випадкові
великі прості числа. Для забезпечення
максимальної безпеки вибирають
– випадкові
великі прості числа. Для забезпечення
максимальної безпеки вибирають
![]() і
і
![]() однакової
довжини й зберігають у секреті.
однакової
довжини й зберігають у секреті.
Множина
![]() з операціями додавання та множення за
модулем
з операціями додавання та множення за
модулем
![]() утворює арифметику за модулем
утворює арифметику за модулем
![]() .
.
Відкритий
ключ
![]() вибирають випадково так, щоб виконувалися
умови:
вибирають випадково так, щоб виконувалися
умови:
![]() (4.6)
(4.6)
![]() , (4.7)
, (4.7)
де
![]() – функція
Ейлера.
– функція
Ейлера.
Функція
Ейлера
![]() вказує
кількість додатних цілих чисел в
інтервалі від 1
до
вказує
кількість додатних цілих чисел в
інтервалі від 1
до![]() ,
які взаємно прості з N
,
які взаємно прості з N
![]() .
.
Умова
(3.7) означає, що відкритий ключ
![]() і функція Ейлера
і функція Ейлера
![]() повинні
бути взаємно простими.
повинні
бути взаємно простими.
Далі,
використовуючи розширений алгоритм
Евкліда, обчислюють таємний ключ
![]() ,
такий, що
,
такий, що
![]() (4.8)
(4.8)
або
![]() .
.
Це
можна здійснити, тому що одержувач B
знає пару простих чисел
![]() і може легко знайти
і може легко знайти
![]() .
Помітимо, що
.
Помітимо, що
![]() й
й
![]() повинні бути взаємно простими.
повинні бути взаємно простими.
Відкритий
ключ
![]() використовують для шифрування даних,
а таємний ключ
використовують для шифрування даних,
а таємний ключ
![]() – для
розшифрування.
– для
розшифрування.
Процес
зашифрування визначає криптограму
![]() через пару (
через пару (![]() ,
М)
у відповідності до формули (4.9).
,
М)
у відповідності до формули (4.9).
(4.9)
Обернення функції
![]() ,
тобто визначення значення M
за відомим значенням
,
тобто визначення значення M
за відомим значенням
![]() практично не здійсненне при N2512.
практично не здійсненне при N2512.
Однак
обернену задачу, тобто задачу розшифрування
криптограми C,
можна вирішити, використовуючи пару
(![]() ,
, ![]() )
за формулою
(4.10).
)
за формулою
(4.10).
![]() .
(4.10)
.
(4.10)
Процес розшифрування можна записати так:
![]() (4.11)
(4.11)
Підставляючи в (4.11) значення (4.9) і (4.10), одержуємо:
![]()
або
![]() . (4.12)
. (4.12)
Відповідно
до теореми Ейлера, яка стверджує, що
якщо
![]()
![]() ,
то
,
то
![]()
або
![]() . (4.13)
. (4.13)
Порівнюючи вираження (4.12) і (4.13), одержуємо
![]()
або, що те саме,
![]() .
.
Саме
тому для обчислення таємного ключа
![]() використовують співвідношення (4.8).
використовують співвідношення (4.8).
Таким чином, якщо криптограму
![]()
піднести до
степеня
![]() ,
то в результаті відновлюється вихідний
відкритий текст М,
тому що
,
то в результаті відновлюється вихідний
відкритий текст М,
тому що
![]() .
.
Отже,
одержувач B,
що створює криптосистему, захищає два
параметри: таємний
ключ
![]() і пару
чисел
і пару
чисел
![]() ,
добуток
яких дає значення модуля N.
З іншого боку, одержувач B
відкриває значення модуля N
і відкритий ключ
,
добуток
яких дає значення модуля N.
З іншого боку, одержувач B
відкриває значення модуля N
і відкритий ключ
![]() .
.
Зловмиснику
відомі лише значення
![]() та N.
Якби він зміг розкласти число N
на множники P
й Q,
то він довідався б "потаємний хід"
– трійку чисел
та N.
Якби він зміг розкласти число N
на множники P
й Q,
то він довідався б "потаємний хід"
– трійку чисел
![]() ,
обчислив значення функції Ейлера
,
обчислив значення функції Ейлера
![]() та визначив значення таємного ключа
та визначив значення таємного ключа
![]() .
.
Однак, як було відзначено раніше, розкладання дуже великого числа N на множники не здійсненно обчислювальними методами (за умови, що довжини обраних Р и Q становлять не менше 100 десяткових знаків).
Процедури шифрування та розшифрування в криптосистемі RSA
Припустимо, що користувач A хоче передати користувачеві B повідомлення в зашифрованому вигляді, використовуючи криптосистему RSA. У такому випадку користувач A є в ролі відправника повідомлення, а користувач B – у ролі одержувача. Як відзначалося вище, криптосистему RSA повинен сформувати одержувач повідомлення, тобто користувач В. Розглянемо послідовність дій користувача В і користувача A.
-
Користувач B вибирає два довільних великих простих числа P й Q.
-
Користувач B обчислює значення модуля N згідно з (4.5).
-
Користувач B обчислює функцію Ейлера
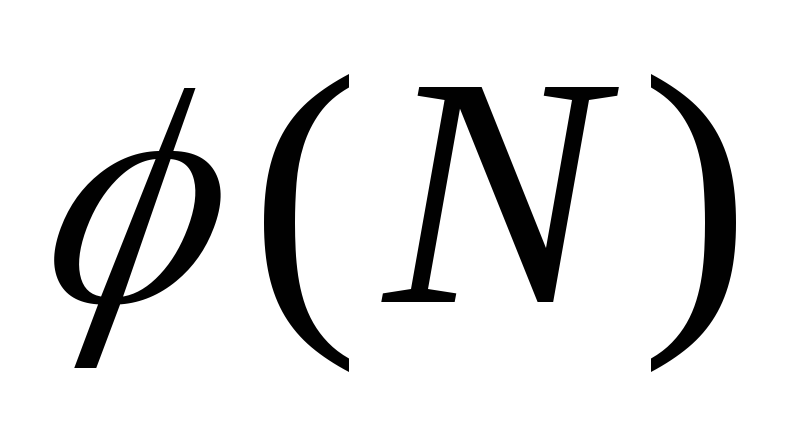 й вибирає значення відкритого ключа
й вибирає значення відкритого ключа
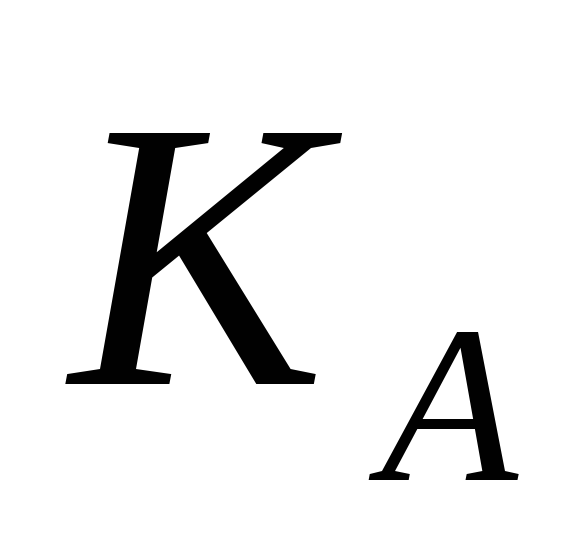 з
урахуванням виконання умов (4.6) і (4.7).
з
урахуванням виконання умов (4.6) і (4.7). -
Користувач B обчислює значення таємного ключа
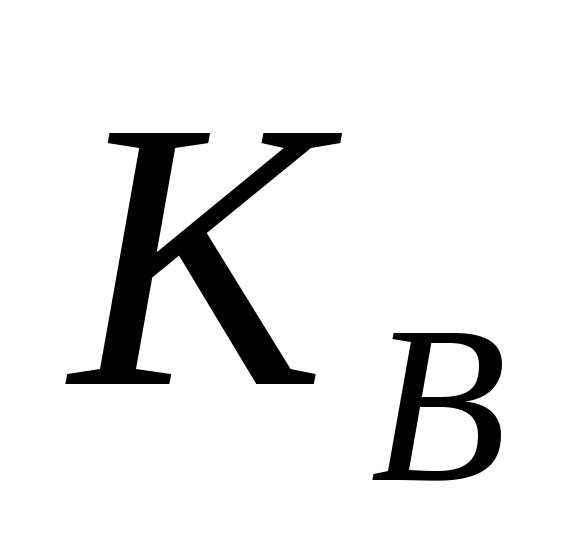 за формулою (4.8),
використовуючи розширений алгоритм
Евкліда.
за формулою (4.8),
використовуючи розширений алгоритм
Евкліда. -
Користувач B пересилає незахищеним каналом користувачу A пару чисел (N,
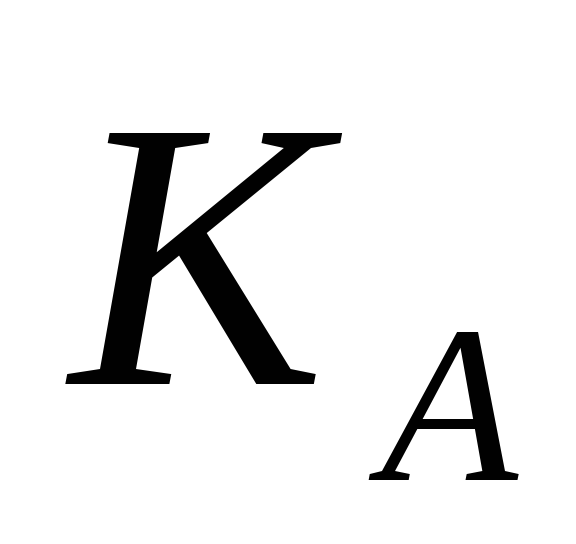 ).
).
Якщо користувач A має бажання передати користувачу B повідомлення М, він виконує такі кроки.
-
Користувач A розбиває вихідний відкритий текст М на блоки, кожний з яких може бути поданий у вигляді числа
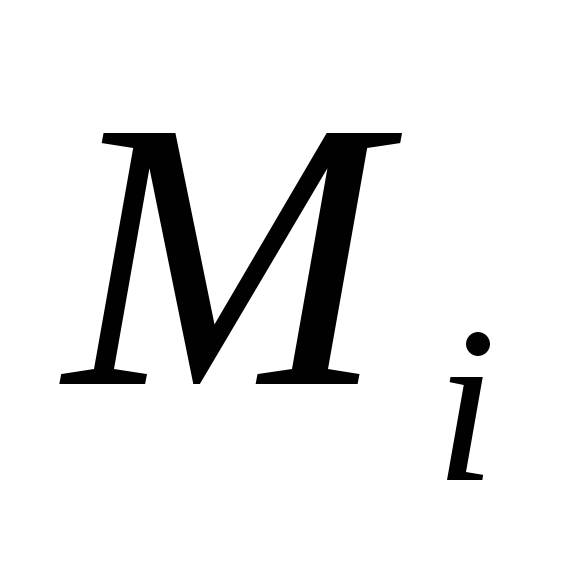 ,
,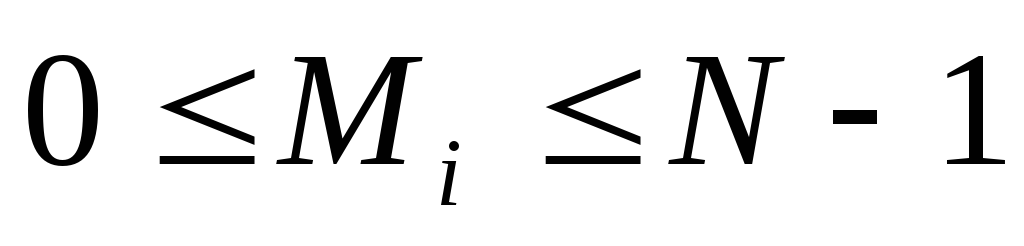 .
. -
Користувач A шифрує текст, поданий у вигляді послідовності чисел М, за формулою
![]()
і відправляє користувачеві В криптограму
![]() .
.
-
Користувач B розшифровує прийняту криптограму
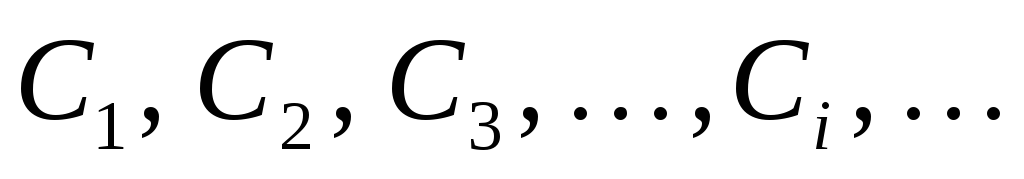 ,
використовуючи таємний ключ
,
використовуючи таємний ключ
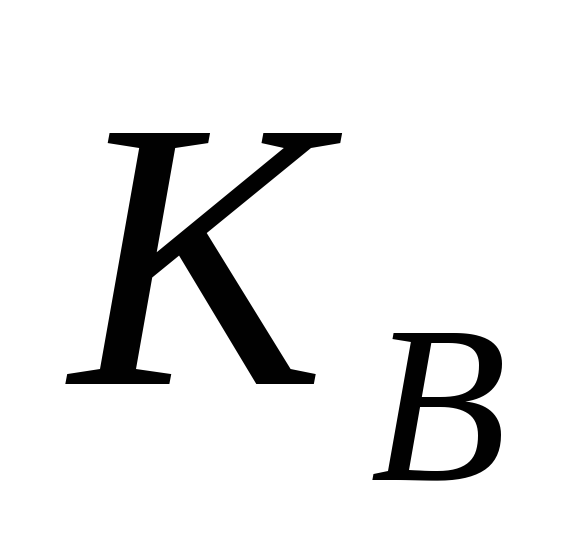 ,
за формулою
,
за формулою
![]() .
.
У
результаті буде отримана послідовність
чисел
![]() ,
які являють собою вихідне повідомлення
М. Щоб
алгоритм RSA мав практичну
цінність, необхідно мати можливість
без істотних витрат генерувати великі
прості числа, вміти оперативно обчислювати
значення ключів
,
які являють собою вихідне повідомлення
М. Щоб
алгоритм RSA мав практичну
цінність, необхідно мати можливість
без істотних витрат генерувати великі
прості числа, вміти оперативно обчислювати
значення ключів
![]() та
та
![]() .
.
Наприклад, виконаємо шифрування повідомлення “Буду завтра”.
Нехай
P=59,
Q=61.
Тоді
![]() ,
а
,
а
![]() .
Виберемо як відкритий ключ
.
Виберемо як відкритий ключ
![]() довільне число з урахуванням виконання
умов (4.6)
і (4.7).
Нехай
довільне число з урахуванням виконання
умов (4.6)
і (4.7).
Нехай![]() . Згідно (4.8) таємний ключ
. Згідно (4.8) таємний ключ
![]() .
.
Подамо повідомлення як послідовність цілих чисел у діапазоні від 1 до 32. Нехай A – 01, Б – 02, В – 03, ..., Я – 32.
Тоді повідомлення “Буду завтра” буде подано у вигляді
02 20 05 20 08 01 03 19 17 01.
Розбиваємо повідомлення на блоки по чотири цифри
0220 0520 0801 0319 1701
і кодуємо кожен блок:

У результаті одержимо шифр 0099 3273 2050 0719 1664.
Для
відновлення вихідного тексту необхідно
обчислити модульну експоненту, підвівши
зашифроване значення
![]() в степінь
в степінь
![]() за модулем N:
за модулем N:
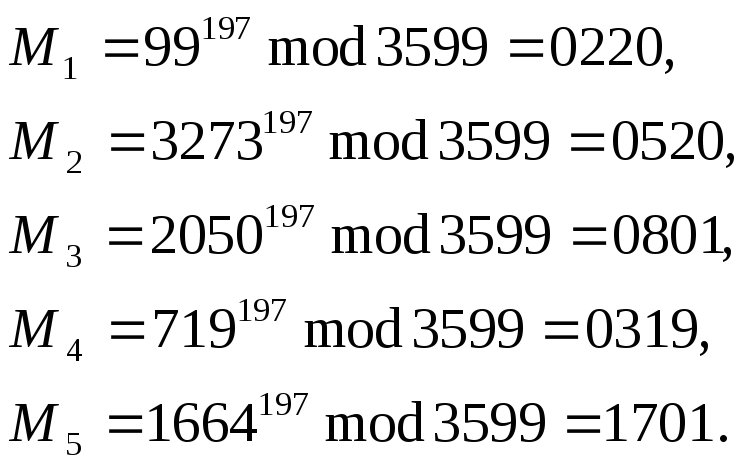
Таким чином, отримали відновлене вихідне повідомлення
0220 0520 0801 0319 1701.
Криптосистеми RSA реалізуються як апаратним, так і програмним шляхом.
Для апаратної реалізації операцій зашифрування та розшифрування RSA розроблені спеціальні процесори. Ці процесори, реалізовані на надвеликих інтегральних схемах, дозволяють виконувати операції RSA, пов’язані з піднесенням великих чисел у колосально великий ступінь за модулем N, за відносно короткий час.
Слід відзначити, що і апаратна, і програмна реалізації алгоритму RSA в декілька сот разів повільніші від реалізацій симетричних криптосистем. Мала швидкодія криптосистеми RSA обмежує сферу її застосування, але не перекреслює її цінність.
Безпека й швидкодія криптосистеми RSA
Безпека
алгоритму RSA базується на труднощах
розв’язання задачі факторизації великих
чисел, що є добутками двох великих
простих чисел. Дійсно, крипостійкість
алгоритму RSA визначається тим, що після
формування таємного ключа
![]() й відкритого ключа
й відкритого ключа
![]() "стираються" значення простих
чисел P
й Q,
і тоді винятково важко визначити таємний
ключ
"стираються" значення простих
чисел P
й Q,
і тоді винятково важко визначити таємний
ключ
![]() за
відкритим ключем
за
відкритим ключем
![]() ,
оскільки для цього необхідно розв’язати
задачу знаходження дільників P
та Q
модуля N.
,
оскільки для цього необхідно розв’язати
задачу знаходження дільників P
та Q
модуля N.
Розкладання
величини N
на прості множники Р
і Q
дозволяє обчислити функцію
![]() ,
а потім визначити таємне значення
,
а потім визначити таємне значення
![]() ,
використовуючи рівняння (4.8).
,
використовуючи рівняння (4.8).
Іншим
можливим способом криптоаналізу
алгоритму RSA є безпосереднє обчислення
або підбір значення функції
![]() .
Якщо встановлено значення
.
Якщо встановлено значення
![]() ,
то співмножники P
й Q
обчислюються досить просто. Справді,
нехай
,
то співмножники P
й Q
обчислюються досить просто. Справді,
нехай
![]()
Знаючи (N), можна визначити х і потім y; знаючи х та y, можна визначити числа P і Q з таких співвідношень:
![]() .
.
Однак ця атака не простіша задачі факторизації модуля N.
Задача факторизації є задачею, яка важко розв’язується для великих значень модуля N.
Спочатку автори алгоритму RSA пропонували для обчислення модуля N вибирати прості числа P й Q випадковим чином, по 50 десяткових розрядів кожне. Вважалося, що такі великі числа N дуже важко розкласти на прості множники. Один з авторів алгоритму RSA, Р.Райвест, вважав, що розкладання на прості множники числа з майже 130 десяткових цифр, наведеного в їхній публікації, зажадає більше 40 квадрильйонів років машинного часу. Однак цей прогноз не виправдався через порівняно швидкий прогрес обчислювальної потужності комп’ютерів, а також поліпшення алгоритмів факторизації.
Один з найбільш швидких алгоритмів, відомих у цей час, алгоритм NFS (Number Field Sieve) може виконати факторизацію великого числа N (із числом десяткових розрядів більше 120) за число кроків, оцінюваних величиною
![]()
У 1994 р. було факторизовано число з 129 десятковими цифрами. Це вдалося здійснити математикам А.Ленстра й М.Манассі за допомогою організації розподілених обчислень на 1600 комп’ютерах, об’єднаних мережею, протягом восьми місяців. На думку А.Ленстра та М.Манассі, їхня робота компрометує криптосистеми RSA і створює більшу погрозу їхнім подальшим застосуванням. Тепер розроблювачам криптоалгоритмів з відкритим ключем на базі RSA доводиться уникати застосування чисел довжиною менше 200 десяткових розрядів. Останні публікації пропонують застосовувати для цього числа довжиною не менше 300 десяткових розрядів.
4 Схема шифрування Поліга - Хеллмана
Схема шифрування Поліга - Хеллмана подібна RSA. Розглянута схема не є симетричним алгоритмом, оскільки використовуються різні ключі для шифрування та розшифрування. З іншого боку її не можна віднести й до класу криптосистем з відкритим ключем, тому що ключі шифрування та розшифрування легко виходять один з одного. Обидва ключі (відкритий і таємний) необхідно тримати в таємниці.
Аналогічно схемі RSA криптограма C і відкритий текст M визначаються зі співвідношень:
![]() , (4.14)
, (4.14)
![]() , (4.15)
, (4.15)
де
![]() . (4.16)
. (4.16)
На
відміну від алгоритму RSA у цій схемі
число N
не визначається через два великих
простих числа; число N
повинне залишатися частиною таємного
ключа. Якщо хто-небудь довідається
значення
![]() та N,
він зможе обчислити значення
та N,
він зможе обчислити значення
![]() .
.
Не
знаючи значень
![]() або
або
![]() ,
зловмисник буде змушений обчислювати
значення
,
зловмисник буде змушений обчислювати
значення
![]() .
.
