
Лекции / 50 лекций по микроэкономике / 50_Ответы на задачи и вопросы
.pdf
Ответы на задачи и вопросы 709
нополии ( QM ) удовлетворяет уравнению MR = a - bQM = c . Так как c есть в то же время минимум средних затрат отдельного завода, в конкуре нтной отрасли уста-
новится равновесная цена, равная c. Равновесный объем для конкурентной отрасли (QC ) удовлетворяет уравнению PD = a - bQC = c . Сравнивая условия равновесия для разных структур, найдем, что QC = 2QM . Так как эффективный размер завода в обоих случаях один и тот же, число заводов в конкурентной отрасли вдвое больше, чем в монополии, т. е. в данном случае оно равно 200.
4а. Если заводы имеют одинаковые функции затрат, то объем вы пуска фирмы (Q) окажется распределенным поровну между заводами, так что на каждый из них
придется объем Q n. Функция затрат фирмы равна |
|
|
|||
æ |
Qö |
|
Q2 |
|
|
TC(Q)= n × TCi ç |
|
÷ |
= 100n + 10Q + |
|
. |
|
n |
||||
è n ø |
|
|
|||
4б. Распределение объемов производства |
между |
заводами хар актеризуется ра- |
||||
венством |
предельных |
10 + 2Q1 |
= |
10 + 0.5 |
× Q2 , откуда |
Q2 = 4Q1 . Òàê |
затрат: |
= 0.8Q . Отсюда |
|
||||
êàê Q = |
Q1 + Q2 , находим Q1 = 0.2Q, Q2 |
|
||||
|
TC(Q)= [100 + 10 × 0.2Q + (0.2Q)2]+ [200 + 10 × 0.8Q + 0.25(0.8Q)2]= |
|||||
|
|
= 300 + 10Q + 0.2Q2 . |
|
|
||
4â. MC1(Q1)= 10 + 2Q1 ; |
MC2(Q2)= 5 + 0.5Q2 . Заметим, что малый объем выпуска |
|||||
не может быть распределен между заводами так, чтобы выпол нялось равенство
MC1 = MC2 |
: òàê êàê MC1 ³ 10 , à MC2 может принимать меньшие значения, малые |
||||
объемы ( Q |
£ 10 ) должны выпускаться только 2-м заводом. При бó льших значениях |
||||
Q равенство предельных затрат дает уравнение |
|||||
|
|
10 + 2Q1 = 5 + 0.5 × Q2 , |
|||
÷òî |
совместно с равенством Q1 + Q2 = Q äàåò |
распределение объема Q1 = 0.2Q - 2; |
|||
Q2 |
= 0.8Q + 2. Èòàê, |
|
|
|
|
|
|
Q |
= ì0, |
|
Q £ 10, |
|
|
1 |
í |
, |
Q > 10; |
|
|
|
î0.2Q - 2 |
||
|
|
Q |
= ìQ, |
|
Q £ 10, |
|
|
2 |
í |
, |
Q > 10. |
|
|
|
î0.8Q + 2 |
||
Опуская промежуточные выкладки, приведем окончательный результат:
ì |
300 + 5Q + 0.25Q2, |
Q £ 10, |
||
TC(Q)= í |
|
2 |
, |
Q > 10. |
î295 |
+ 6Q + 0.2Q |
|||
Êлекции 27
1.Сегменты различаются только масштабами: при любой цене Q1D(P)= 5Q2D(P); следовательно, при любой цене совпадают и эластичности сп роса. Так как предель-
ная выручка и цена связаны соотношением MR = P(1 − 1 η), ãäå h — эластичность спроса, то отсюда следует, что при совпадающих значениях предельной выручки на сегментах будут совпадать также цены спроса. Фирма не мож ет осуществить эффективную ценовую дискриминацию.
η), ãäå h — эластичность спроса, то отсюда следует, что при совпадающих значениях предельной выручки на сегментах будут совпадать также цены спроса. Фирма не мож ет осуществить эффективную ценовую дискриминацию.

710 Ответы на задачи и вопросы
2. На первом сегменте MR1 £ P1D £ 100, но MC ³ 100. Ни при продажах по единой цене, ни при попытке осуществить ценовую дискриминаци ю на первом сегменте покупки совершаться не будут.
3. Распределение выпуска между заводами должно удовлетвор ять условию
MC1(q1)= MC2(q2)= K = MCm(qm)= MC(Q),
где Q — объем выпуска фирмы. С другой стороны, распределение объема продаж между сегментами рынка подчинено условию
MR1(Q1)= MR2(Q2)= K = MRm(Qm)= MR(Q),
чем и исчерпывается доказательство.
4. Прямые функции спроса на сегментах: |
|
QD1 (P)= 60 - 0.2P, |
P £ 300; |
QD2 (P)= 5 - 0.025P, |
P £ 200. |
При продаже продукта по единой цене функция спроса для вс его рынка определяется как сумма функций спроса на сегментах:
ì65 |
- 0.225P, |
P £ 200, |
QD(P)= í |
- 0.2P, |
200 < P £ 300. |
î60 |
Кривая спроса имеет излом при P = 200, Q = 20. Обратная функция спроса:
|
P (Q)= ì300 - 5Q, |
|
Q £ 20, |
|
|||||||
|
|
D |
|
|
í |
|
|
|
|
Q > 20. |
|
|
|
|
|
|
î288.9 - 4.44Q, |
|
|||||
Общая выручка: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì300Q - |
5Q2, |
Q £ 20, |
|
TR Q |
) = |
Q |
× |
P |
Q |
) |
= í |
|
2 |
|
|
( |
|
|
D ( |
|
î288.9Q |
- 4.44Q , |
Q > 20. |
||||
|
|
|
|
|
|
|
|
||||
Предельная выручка: |
|
|
|
|
|
|
|
|
|
|
|
|
MR(Q)= |
ì300 - 10Q, |
|
Q £ 20, |
|||||||
|
í |
|
|
Q > 20. |
|
||||||
|
|
|
|
|
|
î288.9 - 8.89Q, |
|
||||
Для расчетов, связанных с ценовой дискриминацией, нам пон адобятся функции предельной выручки для каждого из сегментов:
MR1(Q)= 300 - 10Q;
MR2(Q)= 200 - 80Q.
Чтобы выполнить «горизонтальное суммирование» соответс твующих кривых, найдем обратные функции:
Q1(MR)= 30 - 0.1MR, MR £ 300;
Q2(MR)= 2.5 - 0.0125MR, MR £ 200,
и их сумму:

|
Ответы на |
задачи и вопросы 711 |
|
|
|
Q(MR) = Q1(MR)+ Q2 |
ì30 - 0.1MR, |
MR £ 200, |
(MR) = í |
|
|
|
î32.5 - 0.1125MR, MR > 200. |
|
Обратная функция представляет собой предельную выручку дискриминирующей фирмы:
ì300 |
- |
10Q, |
Q £ 10, |
MR(Q)= í |
|
- 8.89Q, |
Q > 10. |
î288.9 |
|||
Для нахождения общей выручки требуется проинтегрироват ь предельную выручку; интегрирование придется выполнить раздельно по уч асткам:
0
TR(Q) = ò(300 - 10x)dx = 300Q - 5Q2 , Q £ 10.
0
Отметим, что TR(10)= 2500, и перейдем к интегрированию для второго участка:
0
TR(Q)= TR(10)+ ò(288.9 - 8.89x)dx =
10
= 2500 + 288.9(Q - 10)- 8.89(Q2 - 102)=
= 55.5 + 288.9Q - 8.89Q2 , Q > 10.
Êлекции 28
1.–0.2.
2.Точка равновесия длительного периода — точка касания кр ивыхLAC и спроса; в этой точке одновременно выполняются равенства:
LAC(Q)= PD(Q)
è
dLAC(Q) = dPD(Q). dQ dQ
Следовательно, в этой точке совпадают эластичности средн их затрат и цены спроса по объему; последняя равна –0.2 (см. решение предыдущей задач и). Таким образом,
|
[LAC] = |
|
Q |
|
æ |
|
10 |
ö |
|
E |
|
|
× |
ç |
- |
|
+ 2 |
= -0.2, |
|
|
|
|
|||||||
Q |
|
10 |
Q + 20 + 2Q |
|
|
|
÷ |
|
|
|
|
|
è Q2 |
ø |
|
||||
откуда Q » 117. . В точке равновесия цена и средние затраты совпадают; подс тавляя найденное значение Q в выражение для LAC, найдем, что P » 30.9.
3. Используя решение предыдущей задачи, найдем, что объем от раслевого спроса в условиях монополистической конкуренции равен 1000 Ч 117. = 1170. В условиях совершенной конкуренции равновесная цена равна min LAC = 28.9; соответствующий выпуск фирмы равен 2.24. Зная эластичность отраслевого спро са, найдем, что в условиях совершенной конкуренции объем спроса при равн овесной цене равен 1179(28.9 30.9)−0.5 = 1212. Этот объем производят 1212
30.9)−0.5 = 1212. Этот объем производят 1212 2.24 = 542 фирмы.
2.24 = 542 фирмы.

712 Ответы на задачи и вопросы
Êлекции 30
1.До объединения индекс Херфиндаля—Хиршмана равен 202 + 102 + k32 + k42 + K , ãäå k3 , k4 , ... — рыночные доли остальных фирм; после объединения он при мет значение (20 + 10)2 + k32 + , т. е. увеличится на 900 – 500 = 400 пунктов и будет равен 2100.
2.На остальные фирмы приходится 5 % рыночного объема. Индекс Херфиндаля— Хиршмана лежит в границах от 502 + 302 + 152 = 3625 (в пределе, если фирм очень
много и каждая из долей k3 , k4 , ... ничтожно мала) до 502 + 302 + 152 + 52 = 3650 |
|
(если одна из долей близка к 5 %, а остальные ничтожно малы). |
|
3à. |
1. |
3á. |
2.25. |
К лекции 32
1. Так как фирма продает продукт на конкурентном рынке, для нее MRPx = P·MPx. |
||||||||||||
Находим MP = d(2 |
x )/ |
dx |
= 1 / x |
. Отсюда MRP |
= P / |
x . Из условия MRP |
= p |
x |
||||
x |
|
|
|
P2 |
X |
|
x |
|
||||
находим функцию спроса на ресурс: |
xD = |
. При ценах продукта, указанных |
||||||||||
2 |
||||||||||||
в условии, xD = 25 / px2; |
|
|
|
px |
|
|
|
|
|
|||
100 / px2; |
225 / px2. |
|
|
|
|
|
||||||
2. В отличие от предыдущей задачи здесь MR = 20 – 2q. Подстановка вместо q
производственной |
функции |
|
äàåò |
|
MR = 20 - 4 |
x , |
откуда |
|
MRPx = |
|||||||||
= (20 - 4 |
x)/ x = 20 / |
x - 4 . Из условия MRP |
x |
= p |
x |
находим: x |
= 400 / ( p |
x |
+ 4)2. |
|||||||||
|
= ¶Q / ¶x = 6x−0.7 × y−0.7 |
|
|
|
|
|
|
|
|
D |
|
|
||||||
3. MP |
Åñëè p |
x |
— цена первого фактора, то спрос подчи- |
|||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
нен уравнению |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
x |
= P·MP |
x |
= 30x–0.7·y0.7, |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
èëè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
30ö |
|
|
|
|
|
–1.43 |
|
|
|
|
|
||
|
|
x = |
ç |
|
÷1 / 0.7 ≈129y·px |
|
. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
è |
px ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
При y = 10 спрос описывается равенством x = 1290px–1.43, а при y = 20 — равенством x = 2580px–1.43.
К лекции 33
1. Предельный продукт пряжи MP = ¶q / ¶x = 2 - 0.5x , ценность предельного продукта VMP = P·MP = 20 – 5x. Условие VMP = p позволяет определить функцию спроса фирмы xD = 4 – 0.2p; функция спроса отрасли xD = 400 – 20p.
2. Поскольку цена пряжи в данном случае не является заданно й, необходимо найти совместное равновесие на двух рынках — шерсти и пря жи.
Условие VMP = p позволяет записать функцию индивидуального спроса фирм ы в виде xD = 4 – 2p/P, а функцию отраслевого спроса — в виде xD = 400 – 200p/P.
Определим функцию предложения на рынке пряжи. Производст венная функция фирмы q = 2x – 0.25x2 позволяет определить затраты шерсти на производство q единиц пряжи: x = 4 - 2 4 - q (в силу задания производственной функции x £ 4). Общие затраты фирмы TC = px = p(4 – 2 4 - q ), а предельные затраты MC = = p/ 4 - q . Условие MC = P дает функцию предложения фирмы qS = 4 – (p/P)2, а отсюда функция рыночного предложения пряжи QS = 400 – 100(p/P)2.
Приравнивая заданную функцию спроса на шерсть найденной функции предложения, находим условие равновесия на рынке шерсти:

Ответы на задачи и вопросы 713
æ |
pö 2 |
2 |
|
400 – 100 ç |
|
÷ |
= 400 – P . |
|
|||
è |
Pø |
|
|
Равновесие на рынке шерсти удовлетворяет условию
p
80p – 1100 = 400 – 200 P .
(1)
(2)
Решая систему уравнений (1) и (2), находим: P = 12.5, p = 15.6. Равновесные объемы: Q = 243.75, X = 150.
К лекции 34
|
|
|
|
|
dq |
1. |
MRP = MR·MP = P· dx = 20·1 = 20; |
||||
обратная функция предложения томатов: pS = 5 + x/2; |
|||||
|
ME = |
d |
|
x |
|
|
|
(5 + |
|
) · x = 5 + x. |
|
|
|
2 |
|||
|
dx |
||||
Условие MRP = ME дает 20 = 5 + x, откуда x = 15, p = 12.5. 2. а) P = 50, Q = 20.
б) Появление фирмы-посредника разделяет рынок на два: заку пки производятся по цене p в количестве x, продажа населению — по цене P в количестве Q. На первом рынке фирма выступает в качестве монопсониста, на втором — в качестве монополиста. Ее формальная производственная функция Q = x.
Обратная функция предложения на первом рынке pS = 30 + x, так что для посредника ME = 30 + 2x. Обратная функция спроса на втором рынке PD = 60 – Q/2, и для посредника MRP = 60 – Q. Приравнивая MRP и ME с учетом Q = x, получим Q = = x = 10. Условие предложения на первом рынке дает p = 40, а по условию спроса на втором — P = 55.
3.Задача особенно просто решается графически. Пусть точка E (рис. 13) соответствует конкурентному равновесию. Точка B делит отрезок AE пополам, так что через нее проходит и линия MRP, и линия ME, чем по существу и исчерпывается решение.
4.При цене ресурса p прибыли фирм
определяется выражениями:
p A = 25x – 20 – px, p B =
= px – TCB(x) = px – (30 + 5x + x2). Суммарная прибыль обеих фирм
p A + p B = 25x – 20 – (30 + 5x + x2)
принимает наибольшее значение при x = = 10. Это значит, что при любом фиксированном значении p A наибольшее зна- чение p B достигается при x = 10, и наоборот.

714 Ответы на задачи и вопросы
Фирма A не вступит в сделку, если p A < 0. Следовательно, для ее согласия необходимо p A ³ 0:
25·10 – 20 – p·10 ³ 0, èëè p £ 23.
Для согласия фирмы B необходимо p B ³ 0:
p·10 – (30 + 5·10 + 102) ³ 0, èëè p ³ 18.
Итак, контрактная линия на плоскости (x, p) — отрезок прямой x = 10, ограниченный значениями p = 18 и p = 23.
Êлекции 35
1.а) Определим норму замещения дохода досугом:
¶U |
= |
1 |
, |
¶U |
= |
1 |
0.1 |
, |
¶F |
2 F - 10 |
¶I |
2 |
I |
||||
откуда |
|
|
|
I |
|
|
|
|
|
|
MRS = |
0.1(F - 10) . |
|
|
|
||
Подставляя значения I = 8·10 = 80, F = 24 – 8 = 16, найдем: MRS ≈11.5, что не совпадает со ставкой заработной платы w = 10; состояние работника неравновесное. Так как MRS > w, оценка работником дополнительного свободного времени в ыше ставки заработной платы, и он ощущает нехватку свободного времени.
б) Полученный в предыдущем пункте вывод подтверждается р асчетом оптимальной для работника продолжительности рабочего дня L. В условие оптимума
MRS = w подставим I = wL = 10L; F = 24 – L:
10L
 0.1(14 - L) = 10,
0.1(14 - L) = 10,
откуда L = 7.
Êлекции 36
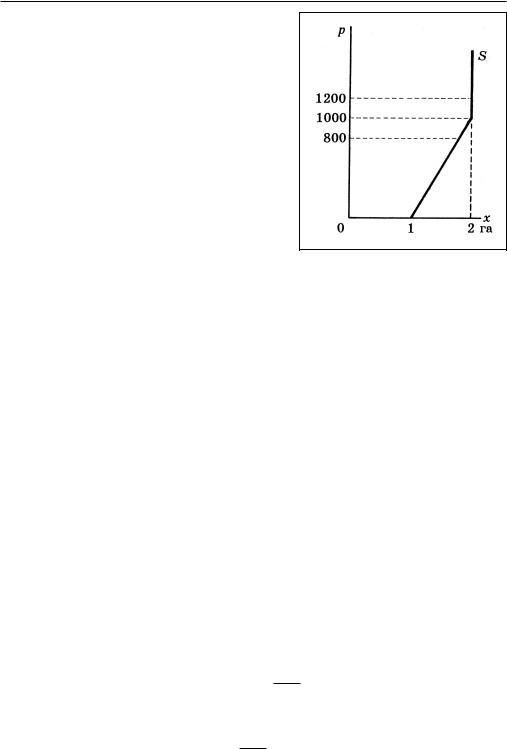
1.а) Часть участка, не требующая орошения, может быть предложена по любой цене; остальная часть — только по цене, покрывающей затраты на орошение. Таким образом,
|
S |
ì5, |
0 < p £ 1000, |
x |
|
= í |
p > 1000 |
|
|
î15, |
(ðèñ. 14).
б) При p = 800 экономическая рента R = = 5·800 = 4000 р./год; удерживающий доход T = 0. При p = 1200 R = 5·1200 + 10·200 = = 8000 р./год, T = 10·1000 = = 10000 р./год.
2. Ни при какой цене субъекту не потребуется более 1 га для дачного участка, так что он
Ответы на задачи и вопросы 715
для дачи может воспользоваться частью своего собственного участка. Платой за использование площади в качестве дачного участка является отказ от получения арендной платы за не сдаваемую в аренду площадь. Поэтому функция предложения xS(p) = 2 – xD(p);
|
S |
ì1 + 0.001p, |
p < 1000, |
x |
|
( p) = í |
p ³ 1000 |
|
|
î2, |
(ðèñ. 15).
При p = 800 сдаваемый участок имеет площадь 1.8 га; экономическая рента R = 800(1 +
+1.8)/2 = 1120; удерживающий доход T = = 800·0.8/2 = 320. При p = 1200 R = 1000(1 +
+2)/2 +200·2 = 1900; T = 1000·1/2 = 500.
Êлекции 37
1.а) Найдем норму замещения текущего потребления будущим:
¶U |
= c |
, |
¶U |
= c . |
|
|
|||
1 |
|
0 |
||
¶c0 |
|
¶c1 |
||
Отсюда MRS0.1 = c1/c0. Равновесие потребителя достигается при MRS0.1 = 1 + r, èëè c1 = (1 + r) c0. Подставляя полученное выражение в бюджетное ограничени е
c0 |
+ |
|
c1 |
= m0 + |
m1 |
, |
|
1 |
+ r |
1 + r |
|||||
|
|
|
|
найдем 2c0 = 100 + 180/(1 + r), èëè c0 = 50 + 90/(1 + r). Функция спроса— предложения — разность между потреблением и доходом тек ущего периода:h =
= c0 – m0 = 90/(1 + r) – 50. |
|
|
б) Потребитель предъявит спрос, если h = 90/(1 + r) – 50 > 0, т. е. если r < 0.8. |
||
Предложению соответствуют значения r > 0.8. |
|
|
в) Спрос потребителя описывается выражением |
|
|
|
ì90 / (1 + r) - 50, |
r < 0.8, |
D = |
í0, |
r ³ 0.8, |
|
î |
|
предложение — |
|
|
|
ì0, |
r £ 0.8, |
S = |
í50 - 90 / (1 + r), |
r > 0.8. |
|
î |
|
2. а) При решении предыдущей задачи получено равенство
2c0
из которого следует
h =
= m0 +
1 é m1
2 êë1 + r
m1 , 1 + r
- m0 ùú .
û

716 Ответы на задачи и вопросы
Òàê êàê m0 > 0, при достаточно больших значениях r величина h окажется отрицательной, каково бы ни было значение m1. Следовательно, при любом сочетании m0 è m1 потребитель выйдет на рынок с предложением, если процентн ая ставка достаточно велика.
Åñëè m1 > m0, то при малых значениях r величина h будет положительной, так что потребитель предъявит спрос при низких процентных ставк ах. Если жеm1 ≤ m0, то тем более m1/(1 + r) ≤ m0, и величина h не будет положительной ни при каких значениях r. Таким образом, если текущий доход больше или равен будуще му, то потребитель не захочет брать деньги в долг ни при каких пр оцентных ставках.
б) Для симметрической функции полезности карта безразлич ия симметрична относительно биссектрисы центрального угла, так что MRS0.1 = 1 ïðè c0 = c1. Условие равновесия потребителя MRS0.1 = 1 + r > 1 может выполняться только в верхней половине карты, при c1 > c0. Пусть m0 > m1. Если бы при этом потребитель взял некоторую сумму взаймы, то оказалось бы, что c0 > m0 > m1 > c1. Но, как мы видели, при c0 > c1 равновесие потребителя не может иметь места. Итак, при m0 > m1 потребитель не предъявит спрос на заемные деньги ни при какой процентной ставке.
Êлекции 38
1.Например, (0, 1210, 1331). При процентной ставке 10 % за период первона- чальная цена равна 2000; в возрасте 1 период цена равна 2200, так что обесценение в первом периоде равно –200.
2.0.1 â ãîä.
3. 150 р./га·год. Арендный доход должен покрывать текущие затраты (50 р./га·год) и первоначальные затраты (1000 р./га· 0.1 год–1 = 100 ð./ãà·ãîä).
4. Ds = As – r·Ps – 1.
Ценность в зависимости от возраста:
Ps = 1000 – 200s.
Отсюда
200 = As – 0.25[1000 – 200(s – 1)],
òàê ÷òî
As = 200 + 0.25[1000 – 200(s – 1)] = 500 – 50s.
Поток доходов равен (500; 450; 400; 350; 300).
Êлекциям 41—42
1.Представим исходную комбинацию благ индивида 1 через избыточный cпрос
X1 = EX1 + 78 è Y1 = EY1. Введем избыточный спрос в функцию полезности индивида и максимизируем ее при наличии бюджетного ограничен ия P(XEX1 + PY EY1).
V1 = (EX1 + 78) EY1 + 2(EX1 + 78) + 5EY1 – l(PXEX1 + PYEY1).
Приравняем частные производные по V1 ê 0:
∂V1 = E + 2 – lP = 0, |
||
∂EX1 |
Y1 |
X |
|
||

Ответы на задачи и вопросы 717
|
∂V1 |
= E + 83 – lP = 0, |
||||
|
∂EY1 |
|||||
|
X1 |
Y |
|
|||
|
|
|
|
|||
∂V1 |
= – ( P E |
+ P E |
) = 0, |
|||
∂λ |
||||||
|
X X1 |
Y Y1 |
|
|||
Решаем систему уравнений и получаем функции избыточного спроса для индивида 1:
l = |
EX1 + 83 |
= |
EY1 |
+ 2 |
– P1EX1 |
– P2 EY1 |
= 0, |
PY |
|
PX |
|||||
|
|
|
|
|
|||
PYEY1 + PY2 = PXÅÕ1 + PX83,
EX1 = –PYEY1/PX,
EY1 = (PXÅX1 + PX83 – PY2)/PX,
Ex1 = – (PXÅX1 + PX83 – PY2)/PX,
EX1 = PY/PX – 41.5,
EY1 = 41.5 PX/PY – 1.
Таким образом, избыточный спрос представлен как функции о т соотношения цен. Увеличение PX относительно PY уменьшит EX1 и увеличит EY1. Увеличение PY относительно PX увеличит EX1 и уменьшит EY1.
Аналогичным образом поступаем с функцией полезности инд ивида 2.
В итоге решения новой системы уравнений получаем следующ ие функции избыточного спроса для индивида 2:
EX2 = 84 PY/PX – 1,
EY2 = PX/PY – 84.
В соответствии с требованиями «расчищения» рынка можно з аписать:
ÅX = EX1 + EX2 = 85 PY/PX – 42.5 = 0, EY = EY1 + EY2 = 42.5 PX/PY – 85 = 0.
При решении первого из уравнений имеем PY/PX = 0.5, а при решении второго — PX/PY = 2, что, как видно, одно и то же.
Подставляем соотношения цен в индивидуальные функции из быточного спроса и получаем
EX1 = –41; EX2 = 82; EY1 = 41; EY2 = –82.
Индивид 1 отдает 41 ед. блага X индивиду 2 в обмен на 82 ед. блага Y. Cледовательно, парето-эффективная комбинация благ:
X1 = 37, X2 = 41, Y1 = 82, Y2 = 82.
2. Максимизируем прибыли каждой из фирм для нахождения равновесной ставки заработной платы.

718 Ответы на задачи и вопросы
p |
A |
= P X – wl |
X |
|
= 20·10l 1/2 |
– wl , |
|
|
|||||
|
|
X |
|
|
|
X |
|
X |
|
|
|||
¶p A / ¶lX = 100lX–1/2 |
– w = 0 |
Þ lX–1/2 |
= w/100 |
Þ lX = 10000/w2, |
|||||||||
p |
B |
|
= P Y – wl |
Y |
= 10·8l 1/2 |
– wl , |
|
|
|||||
|
|
|
Y |
|
|
|
Y |
|
Y |
|
|
||
¶pB / ¶lY = 40l |
–1/2 |
– w = 0 |
|
Þ l –1/2 |
= w/40 |
Þ l |
Y |
= 1600/w2. |
|||||
Y |
|
|
|
|
|
|
Y |
|
|
|
|
||
Теперь можно составить и решить следующую систему уравне ний:
lX = 10000/w2, lY = 1600/w2, lX + lY = 100.
В результате решения получаем: w* = 10.77.
Далее находим lX* = 10000/10.772 = 86.2 è lY* = 100 – 86.2 = 13.8.
Отсюда X* = 92.85 è Y* = 29.71
Теперь перейдем к нахождению доходов и оптимальных объем ов потребления индивидов.
Мы знаем, что оптимум потребителя в экономике с ценами дос тигается тогда,
когда |
MRS1 |
= |
MRS2 |
= P /P . |
|
XY |
|
XY |
X Y |
Найдем |
|
= MUX1 / MUY1 = Y1/X1 и составим следующую систему урав- |
||
нений: |
|
|
|
|
Y1/X1 = 2,
I1 = PXX1 + PYY1.
I1 — сумма «трудового дохода» и прибыли от фирмы А.
«Трудовой доход» равен 50w* = 50·10.77 = 538.5, p A = 20·92.85 – 10.77·86.2 = = 1857 – 928.37 = 928.63
Cледовательно, I1* = 538.5 + 928.63 = 1467.13.
В результате для индивида 1 можно составить следующую сис тему уравнений:
Y1 = 2X1,
1467.13 = 20X1 + 10Y1.
Ее решение дает X1* = 36.68; Y1* = 73.36.
Аналогичным образом поступаем и в отношении индивида 2.
MRSXY2 = MUX2 / MUY2 = 3Y2/X2.
Его доход I2* = p B + 50w
p B = 10·29.71 – 10.77·13.8 = 297.1 – 148.63 = 148.47,
I2* = 148.47 + 538.5 = 686.97.
Система уравнений для индивида 2:
Y2 = 2/3·X2,
