
Лекции / 50 лекций по микроэкономике / 50_III. Выпуклые множества и функции
.pdf
III. Выпуклые множества и функции 569
3.Все функции одной переменной с постоянной эластичность ю имеют вид (8) (воспользоваться равенством (4)).
4.Функции нескольких переменных с постоянными частными эластичностями — это степенные функции вида
y= Ax1B1x2B2,...,xNBN .
III.Выпуклые множества и функции
При исследовании экономических явлений математическими методами весьма значительным оказывается такое свойство м ногих множеств и функций, как выпуклость. Характер поведения мн огих экономических объектов связан с тем. что определенные зав исимости, описывающие эти объекты, являются выпуклыми. С выпукл о- стью функций и множеств часто связано существование или е динственность решения экономических задач: на этом же свойст ве основаны многие вычислительные алгоритмы.
Справедливость многих утверждений, относящихся к выпукл ым множествам и функциям, совершенно ясна, они почти очевидн ы. В то же время их доказательство зачастую очень сложно. Поэтому здесь будут изложены некоторые основные факты, связанные с выпу клостью, без доказательств, в расчете на их интуитивную убедит ельность.
1. Выпуклые множества на плоскости
Любая геометрическая фигура на плоскости может рассматр иваться как множество точек, принадлежащих этой фигуре. Одни множества (например, круг, прямоугольник, полоса между параллел ьными прямыми) содержат и внутренние, и граничные точки; другие ( например, отрезок, окружность) состоят только из граничных точе к.
Множество точек на плоскости называется выпуклым, если он о обладает следующим свойством: отрезок, соединяющий любые две точки этого множества, целиком содержится в этом множестве (рис . 1).
Примерами выпуклых множеств являются: треугольник, отрезок, полуплоскость (часть плоскости, лежащая по одну сторону от какой-либо прямой), вся плоскость. Другие примеры выпуклых множеств приведены на рис. 2,а. На рис. 2,б приведены примеры невыпуклых множеств.
Множество, состоящее из одной-единственной точки, и пусто е множество, не содержащее ни одной точки, по принятому соглаше нию, также считаются выпуклыми. Во всяком случае, в этих множес твах невозможно провести отрезок, соединяющий какие-то точки э тих множеств и не принадлежащий этим множествам целиком, — в них

570 Математическое приложение
Рис. 1. Отрезок, соединяющий любые две точки выпуклой фигуры , содержится в ней целиком.
Рис. 2. Выпуклые (а) и невыпуклые (б) множества на плоскости.
вообще невозможно выбрать две точки. Поэтому их включение в число выпуклых множеств не приведет к противоречию с опре делением, а для математических рассуждений этого достаточно.
Пересечение, т. е. общая часть двух выпуклых множеств, всегда выпукло: взяв любые две точки пересечения (а они — общие, т. е. принадлежат каждому из пересекающихся множеств) и соедин ив их отрезком, мы легко убеждаемся в том, что все точки отрезка я вляются общими для обоих множеств, так как каждое из них выпукло. Вы - пуклым будет и пересечение любого числа выпуклых множест в.
Важным свойством выпуклых множеств является их отделимость: если два выпуклых множества не имеют общих внутрен них точек, то плоскость можно разрезать по прямой таким образ ом, что одно из множеств будет целиком лежать в одной полупло скости, а другое — в другой (на линии разреза могут располагат ься точки обоих множеств). Отделяющая их прямая в одних случая х оказывается единственно возможной, в других — нет (рис. 3).
Граничная точка любого выпуклого множества сама может ра с- сматриваться как выпуклое множество, не имеющее с исходным множе-
Рис. 3. Отделяющие прямые. Рис. 4. Опорные прямые.

III. Выпуклые множества и функции 571
ством общих внутренних точек, следовательно, она может быть отделена от него некоторой прямой. Прямая, отделяющая от выпуклого множества его граничную точку, называется опорной прямой этого множества в данной точке. Опорные прямые в одних точках контура могу т быть единственными, в других — не единственными (рис. 4).
Введем на плоскости систему декартовых координат х, у. Теперь у нас появилась возможность рассматривать различные фиг уры как множества таких точек, координаты которых удовлетвор яют тем или иным уравнениям или неравенствам (если координат ы точки удовлетворяют какому-либо условию, будем для кратко сти говорить, что сама точка удовлетворяет этому условию).
Упражнение 1
Рассмотрите фигуры, точки которых удовлетворяют неравен ствам: а) y ³ x2; á) xy ³ 1; â) xy ³ 1, õ > 0; ã) |õ| + |ó| £ 2;
ä) (õ+1)2 + (ó – 2)2 £ 9. Какие из них выпуклы?
Линейному уравнению ах + by = с удовлетворяют точки прямой. Иными словами, прямая является решением этого уравнения. Решением линейного неравенства
àõ + by ³ ñ |
(1) |
является полуплоскость (проверьте!). |
|
Рассмотрим систему из N неравенств вида |
(1): |
aix + bif ³ ci, i = 1, 2, ..., N. |
(2) |
Решением каждого из неравенств является полуплоскость. Р ешение системы — это множество точек, каждая из которых удовл етворяет всем неравенствам системы, т. е. решение системы неравенств — это пересечение всех решений отдельных неравенств, составляющих систему. Полуплоскость — выпуклое множество, а пересече- ние выпуклых множеств всегда выпукло. Таким образом, решение системы (2) — выпуклое множество. На рис. 5 показано решение системы неравенств
ì |
x - y ³ -1; |
ï |
x + 2y ³ 5; |
í |
ïî- 2x - y ³ -7.
Рис. 5. Решение системы из трех линейных неравенств.
572 Математическое приложение
Заметим, что неравенство ах + by £ с может быть заменено равносильным ему неравенством –ах – by ³ –с, имеющим вид (1). Кроме того, уравнение ах + by = с равносильно такой паре неравенств:
{ax + by ³ c; ax + by £ c.
Таким образом, решение системы линейных уравнений и неравенств — всегда выпуклое множество.
Упражнение 2
Будет ли решение системы
aix + biy > ci, i = l, 2, ..., N
выпуклым множеством? Чем оно отличается от решения систем ы (2)?
Упражнение 3
Придумайте системы неравенств, решениями которых будут: а ) параллелограмм; б) внутренность угла; в) полоса между двумя параллельными прямыми; г) единственная точка; д) пустое множество.
2. Выпуклые функции одной переменной
Проще всего определить выпуклую функцию геометрически. Д ля этого полезно ввести понятие надграфика функции. Надграфиком функции называется множество точек, расположенных над графиком ф ункции и на самом графике. Более строго, надграфик функции f(х) — это множество таких точек, координата х которых лежит в области определения функции, а координата у удовлетворяет неравенству у ³ f(x).
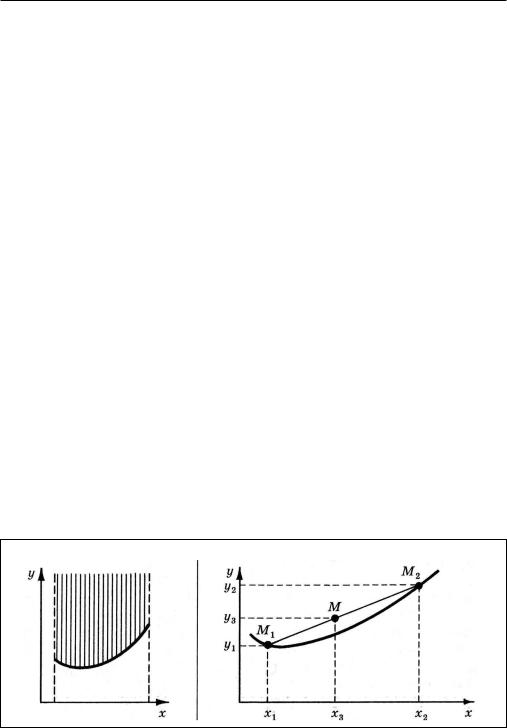
Функция называется выпуклой вниз, если ее надграфик — выпуклое множество. Рис. 6 иллюстрирует это определение.
Рис. 6. Надграфик выпуклой функции.
Рис. 7. Точка хорды не может располагаться ниже графика.

III. Выпуклые множества и функции 573
Приведенное определение является вполне строгим и может быть однозначно переведено на аналитический язык.
Во-первых, функция f(х) должна иметь выпуклую область определения — отрезок, луч или всю прямую.
В противном случае надграфик распался бы на несколько отдельных областей, и отрезок, соединяющий точки из разных о бластей, проходил бы через «запретную зону».
Для выяснения того, какому условию должны отвечать значе- ния выпуклой вниз функции f(x) «выберем какие-либо две точки M1 è M2 на ее графике и проведем хорду M1 M2 (рис. 7). Она целиком должна лежать в надграфике, т. е. надграфику должна принадлежать любая точка М хорды.
Рассмотрим число l, показывающее, в какой пропорции точка M делит хорду:
l = M2M .
M2M1
Эта величина лежит в пределах 0 £ l £ 1. Ясно, что в такой же пропорции абсцисса и ордината точки М делят отрезки [x1, õ2] è [ó1, ó2]:
õ2 – õ3 = l·(õ2 – x1); y2 – y3 = l·(y2 – y1);
èëè
õ3 = l·x1 + (1 – l)õ2; y3 = l·y1 + (1 – l)y2.
Условие принадлежности точки ние неравенства y3 ³ f(õ3). А так неравенство можно представить в
М надграфику — это выполне- âèäåêàê y1 = f(x1), y2 = f(õ2) — ýòî
lf(x1) + (1 - l)f(x2 ) ³ f(lx1 + (1 - l)x2). |
(3) |
Если неравенство (3) выполняется для любых значений x1 è õ2, то любая хорда лежит в надграфике, тем более в надграфике л ежит любой отрезок, соединяющий точки, расположенные выше.
Таким образом, функция f(х), заданная на выпуклом множестве, выпукла вниз, если она обладает следующим свойством: для л ю- бых двух чисел x1 è õ2 из области определения функции и любого числа l из отрезка [0, 1 ] выполняется неравенство (3).
Неравенство (3) часто записывают в «симметричном» виде
l1f(x1 ) + l2f(x2 ) ³ f(l1x1 + l2x2 ), |
(4) |

574 Математическое приложение
Рис. 8. Функции: выпуклая вниз (а), выпуклая вверх (б), не имеющая постоянного знака выпуклости (в).
ãäå
l1 ³ 0, l2 ³ 0, |
l1 + l2 = 1. |
Аналогично можно определить и функции, выпуклые вверх: дл я этого нужно знаки неравенства (3) и (4) заменить на противоположные.
Функции, выпуклые вниз, часто называют просто «выпуклыми» . Выпуклые функции обладают свойством более общим, чем нера венство (4). Если x1, õ2,..., xN — произвольные значения аргумента l1, l2,...,
lN — неотрицательные числа, сумма которых равна единице, то
N |
æ N |
ö |
ålif(xi ) ³ fçålixi÷. |
||
i=1 |
è i=1 |
ø |
Выберем четыре значения аргумента x1 < õ2 < õ3 < õ4 è ïðî- |
|||||||||
ведем хорду M1M4 (ðèñ. 9). |
|
|
|
|
|
|
|
|
|
Промежуточные точки M2 è Ì3 |
лежат в надграфике, так что угол |
||||||||
|
наклона хорды M M * не больше, |
||||||||
|
а хорды М *M |
|
1 |
2 |
|
|
|||
|
|
— не меньше, чем |
|||||||
|
|
3 |
4 |
|
M M * |
ê îñè |
|||
|
угол наклона хорды |
||||||||
|
|
|
|
|
|
1 |
4 |
|
|
|
абсцисс (углы наклона — с учетом |
||||||||
|
знаков!). Следовательно, |
скорость |
|||||||
|
возрастания выпуклой функции в |
||||||||
|
области «больших» значений ар- |
||||||||
|
гумента (на участке [х3, õ4]) íå |
||||||||
|
меньше, чем в области «малых» |
||||||||
|
значений ( [x1, x2]). Переходя к |
||||||||
|
пределам |
ïðè |
|
x2 ® x1 è |
õ4 |
® õ3, |
|||
|
найдем, |
÷òî |
|
f¢(x3 ) |
³ f¢(x1), |
ò. å. |
|||
|
|
||||||||
Рис. 9. Хорда, проведенная в области |
производная |
f |
¢(x) дифференциру- |
||||||
емой выпуклой функции f(х)— не- |
|||||||||
больших значений аргумента, имеет |
|||||||||
больший угол наклона, чем хорда в |
убывающая функция. |
|
|
области малых значений. |
|
III. Выпуклые множества и функции 575
Если производная f¢(x) дифференцируема (т. е. выпуклая функция f(х) дважды дифференцируема), то f¢¢(x) ³ 0. Для дважды дифференцируемых функций это неравенство оказывается р авносильным приведенному выше определению выпуклой функции ; в курсах математического анализа выпуклость обычно опред еляют по знаку второй производной. Но в экономических приложени ях, где часто приходится иметь дело с функциями, графики кото рых имеют изломы, такое определение оказывается мало полезны м.
Если f(х) и g(x) — выпуклые функции и а ³ 0, то выпуклыми будут функции
à) àf(õ);
á) f(x) + g(x);
â) max(f(õ), g(x)).
Выпуклость функций в а) и б) проверяется непосредственно с помощью неравенства (3) или (4). Функция в) при каждом х принимает значение, равное большему из значений f(х) и g(x) (и любому из них, если они равны). Надграфик функции max(f(x), g(x)) есть пересечение надграфиков функций f(х) и g(x) (проверьте!) — отсюда и выпуклость функции в).
Упражнение 4
Существуют ли функции, выпуклые вниз и выпуклые вверх одновременно?
Упражнение 5
Êак выглядит график функции f(х) = = mах (0, а + bх) при различных значе- ниях параметров а и b? Выпуклы ли эти функции?
Упражнение 6
Выпукла ли функция
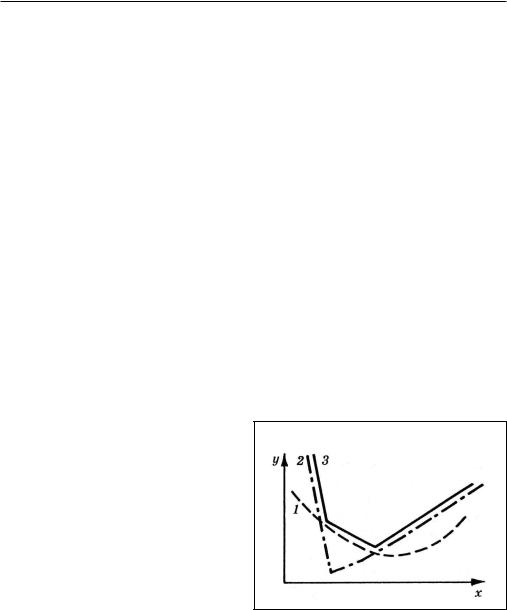
Рис. 10. Графики функций f(х) (1), g(x)
N (2) è max(f(x), g(x)) (3). f(x) = åfi (x),
i=1
ãäå
fi(x) = max (0, ai + bix)?
Как выглядит ее график?

576 Математическое приложение
Упражнение |
7 |
|
|
|
Рассмотрим |
функцию |
|
|
|
|
ìax, |
x < 0; |
||
|
ï |
1 |
|
|
|
ï |
x, |
0 £ x < 1; |
|
|
f(x) = í |
|
||
|
2 |
|||
|
ïï |
1 |
+ b × (x - 1), x ³ 1. |
|
|
2 |
|||
|
î |
|
|
|
При каких значения а и b эта функция
—выпукла вниз?
—выпукла вверх?
—не имеет постоянного знака выпуклости?
IV. Пространство благ
Основные понятия
Многие теоретические вопросы обсуждаются в нашем учебни ке применительно к случаю двух продуктов. В качестве удобного средства, существенно упрощающего их анализ, использовались г рафические построения, в которых набор, включающий два продукта в коли- чествах x1, è x2 изображался точкой на плоскости с декартовыми координатами (x1, x2). Перевод теоретических понятий на геометри- ческий язык делал свойства обсуждаемых явлений весьма на глядными и при этом не приводил к потере строгости: все геометрические понятия (прямые, кривые, углы наклона и т. п.) имели точно определенные аналитические эквиваленты — уравнения, производные, с оотношения между параметрами и т. д. Поэтому такие построения широко используются и в учебниках по экономике, и в научных публикациях.
Однако эти геометрические рассуждения были строгими и то ч- ными лишь для случаев, когда перечень потребляемых благ в клю- чал всего два наименования. В действительности же число б лаг, которыми пользуются люди, значительно больше. Выводы, пол у- ченные геометрическим путем, можно считать обладающими д остаточной общностью, если их удастся распространить на слу чаи произвольного числа благ.
Будем считать, что мы присвоили всем мыслимым благам номера i = 1,2,..., n, и xi обозначает количество i-того блага. Тогда набор благ Х может быть представлен n числами, расположенными
в порядке номеров благ: |
|
X = (x1,x2,...,xn ). |
(1) |
