4. Потенциальная энергия центральных сил

Определение: силы, действующие только по прямой, соединяющей

частицы, и зависящие только от расстояния между ними, называются

центральными. Следовательно, общим для центральных сил будет следующий

силовой закон:

Работа любой центральной силы будет:

,

следовательно, результат интегрирования не зависит от пути и определяется

лишь начальным r₁ и конечным r₂ положениями траектории:

.

Поэтому любая центральная сила является консервативной, и частица в поле центральных сил обладает потенциальной энергией. Примерами центральных сил могут служить гравитационная, кулоновская и упругая силы.

5. Градиент потенциальной энергии

Консервативная сила выражается через потенциальную энергию

следующим образом:

.

Введем дифференциальный оператор градиент (grad) или "набла"

() -- это одно и то же.

.

Зная потенциальную энергию частицы, можно простым дифференцированием найти действующую на нее консервативную силу:

.

Наоборот, по выражению для силы можно интегрированием найти потенциальную энергию частицы.

Эквипотенциальные поверхности.

Геометрическое место точек, в которых потенциальная энергия (или

потенциал) одинакова, называется эквипотенциальной поверхностью. Уравнение такой поверхности имеет вид: .

При перемещении по этой поверхности dU=0, и из выражения следует, что проекция силы на эквипотенциальную

поверхность F_l всегда равна нулю.

Поэтому вектор силы всегда перпендикулярен эквипотенциальной

поверхности.

Вектор силы направлен в сторону убывания (уменьшения)

потенциальной энергии, и в этом же направлении под действием этой силы

будут ускоряться все тела.

Вывод: grad U -- это вектор, направленный по нормали к эквипотенциальной поверхности в сторону возрастания U и равный по величине наибольшей скорости изменения потенциальной энергии в пространстве: .

6. Механическая энергия частицы и закон ее изменения

Сумма кинетической и потенциальной энергий частицы называется ее

полной механической энергией: E=K+U.

Если на частицу действуют только консервативные силы, то с одной стороны, по определению dA=-dU, а с другой стороны, как следствие второго закона Ньютона, dA=dK. Поэтому -dU=dK или d(U+K)=dE=0.

Иначе говоря, механическая энергия частицы, подверженной действию только консервативных сил, сохраняется.

Неконсервативные силы

Неконсервативными называются силы, работа которых зависит от длины и формы пути. Примерами неконсервативных сил являются: сила трения скольжения (но не трение покоя), вязкие силы, силы Ампера и Лоренца.

Пусть на частицу действуют как консервативные, так и неконсервативные силы.

dE=d(K+U)=dA_неконс

Изменение полной механической энергии частицы равно работе всех неконсервативных сил.

.

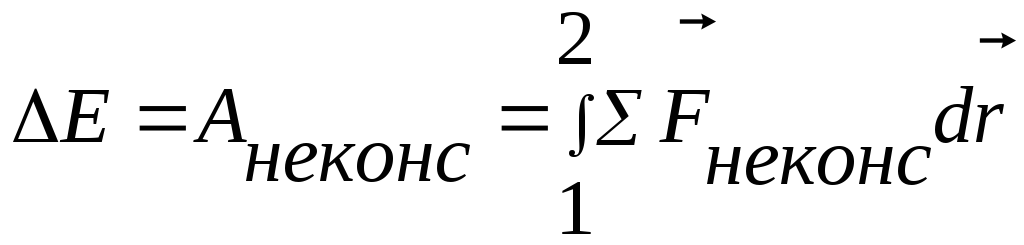При этом изменение механической энергии в замкнутой системе компенсируется изменением тепловой, химической и других видов энергии.

Важным частным случаем неконсервативных сил являются диссипативные силы. Это -- силы, зависящие от скорости частицы и направленные против скорости:

,

например, сила вязкого трения. При действии диссипативных сил

механическая энергия всегда убывает (и превращается во внутреннюю).