Интерференция электромагнитных волн

1 Интерференция когерентных волн

Интерференция волн - это явление устойчивого увеличения или

уменьшения результирующей амплитуды колебаний при суперпозиции

(наложении) двух или более когерентных волн. При этом в разных

точках пространства результирующая амплитуда различна, но в

любой точке она остается постоянной в течение довольно большого

промежутка времени (времени наблюдения).

(Примером интерференции волн являются стоячие волны.)

Пусть в некоторую точку пространства, обычно называемую точкой наблюдения и обозначаемую буквойP, приходят от разных источников две волны с одинаковой частотой и с одинаковым направлением колебаний электрических векторов и . Тогда, согласно принципу

суперпозиции, результирующее колебание в точке P будет иметь вид

,

причем начальные фазы колебаний ибудут зависеть от координат источников и точки наблюдения.

Для сложения колебаний применим метод векторной диаграммы.

,

так как .

Волны называются некогерентными, если их разность фаз

зависит от времени. Тогда среднее значение быстропеременной гармонической функции за время наблюдения , и среднее значение квадрата амплитуды результирующего колебания

.

Интенсивность (или энергия) волны (а для света - освещенность

экрана) пропорциональна квадрату ее амплитуды, т.е. .

Поэтому при наложении некогерентных волн их интенсивности

складываются, и результирующая (усредненная) интенсивность будет

одинакова во всех точках пространства : .

Когерентными называются волны, для которых разность фаз постоянна во времени .

В тех точках пространства (экрана), где разность фаз когерентных волн равна нечетному числу , т.е.

, где m - целое число ( условие минимума ),

результирующая амплитуда будет минимальной и равной

.

В тех же точках, где разность фаз когерентных волн равна четному

числу , т.е.

, где m - целое число (условие максимума ),

результирующая амплитуда будет максимальной: .

Таким образом, при сложении когерентных волн наблюдается

интерференционная картина, состоящая из устойчивых максимумов и

минимумов интенсивности (освещенности) экрана.

Если амплитуды интерферирующих волн одинаковы: ,

в точках минимума освещенность падает до нуля, а в точках максимума

возрастает в четыре раза: .

2 Интерференция света в тонких пленках

Пусть пленка с показателем преломления n, находящаяся в воздухе,

имеет всюду одинаковую толщину d.

Пучок света 1, падая на пленку под углом , частично отражается от оптически более плотной среды со сдвигом фазы на  (т.е. с изменением разности хода на - так называемая "потеря полуволны"), образуя пучок 1'. Но, частично преломляясь, он отражается от нижней поверхности пленки ( в данном случае - без потери полуволны ) и выходит из нее в виде пучка 1'' параллельно пучку 1'.

Пучки света 1' и 1'' когерентны, так как образуются из одного пучка 1, и поэтому могут интерферировать на экране, если их собрать с помощью линзы (роль линзы может выполнять и глаз наблюдателя, что

обычно и происходит).

Оптическая разность хода световых пучков .

Максимумы освещенности для данной длины волны будут наблюдаться при отражении света под определенными углами_max, получаемыми из условия

.

Получаемая таким образом интерференционная картина называется

полосами равного наклона.

Если пленка имеет переменную толщину d, а свет падает на нее

практически нормально, то условие усиления отраженного света с длиной волны имеет вид :

.

Усиление света происходит в тех точках, где пленка имеет определенную величину, удовлетворяющую этому условию. Такая интерференционная картина называется полосами равной толщины.

3. Многолучевая интерференция.

Дифракционная решетка

Практический интерес представляет интерференция не двух, а

большего числа когерентных пучков. Например, интерференция в системе, называемой дифракционной решеткой. Это - система из N одинаковых щелей, расположенных на равном расстоянии d (постоянная решетки) друг от друга. При нормальном падении на решетку плоского волнового фронта с длиной волны каждая щель будет когерентным источником, излучающим свет во всех направлениях. Линза (роль которой может выполнять глаз) соберет параллельные пучки света в одну точкуP экрана (параллельные пучки, распространяющиеся в других направлениях, будут собраны в других точках экрана). Разность хода волн, приходящих от соседних щелей, равна

, т.е. колебания вектора от каждой последующей щели сдвинуты по фазе на

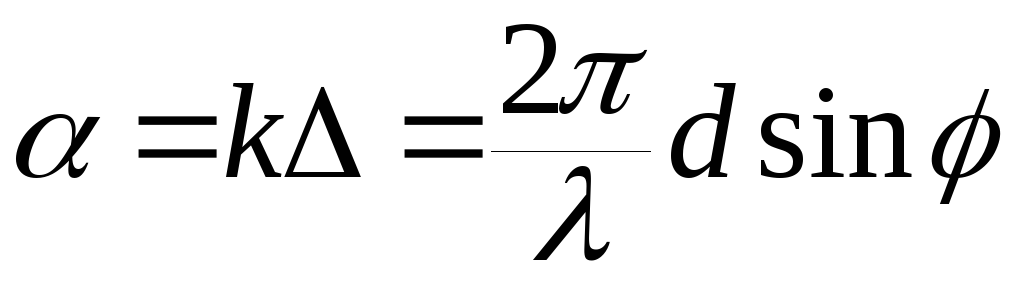
по сравнению с колебаниями от предыдущей щели.

Следовательно,

,

(так как амплитуды колебаний в световой волне, приходящей от каждой щели, одинаковы).

Складывая эти колебания методом векторной диаграммы определяем главные максимумы интенсивности света, прошедшего через дифракционную решетку. Они получаются из условия , где m - целое число.

При выполнении этого условия, т.е. в точках экрана, соответствующих условиям главных максимумов, интенсивность света возрастает по сравнению с интенсивностью света, приходящего от одной щели, враз :

(Решетку можно изготовить, нанеся на основу

штрихов - тогда яркость света возрастет

в раз !)

Но между соседними главными максимумами расположены (N-1) минимумов интенсивности, соответствующих нулям числителя :

, где m - целое число, не равное

- условие дополнительных минимумов. Получаемая при этом интерференционная картина такова :

очень яркие и узкие линии, соответствующие главным максимумам для света с длиной волны , разделены участками, где интенсивность света очень мала из-за наличия дополнительных минимумов. Если на решетку направить белый свет с разными длинами волн, то она разделит его на все цвета радуги, образуя спектры порядкаm.

По критерию Рэлея два пика интенсивности еще можно увидеть раздельно, если минимум первого пика совпадает с максимумом второго, т.е. или

.

Отношение называется разрешающей способностью ди-фракционной решетки. Из этой формулы следует, что разрешающая способность пропорциональна числу щелей N. Чем больше N , тем более узкие и яркие линии получаются в интерференционной картине.