Волновые процессы. Электромагнитные волны

1. Волновая функция

Соседние частицы среды взаимодействуют друг с другом, и если одна частица начнет колебаться, то эти колебания передаются

остальным частицам с некоторой скоростью v. Процесс распространения таких колебаний в пространстве называется волной.

Волны бывают продольные и поперечные. В продольных волнах частицы колеблются (смещаются) вдоль направления распространения волны, т.е. вдоль вектора скорости волны.

Пример: колебания плотности среды, звук.

В поперечных волнах смещение частиц среды перпендикулярно к направлению распространения волны. Продольные волны возникают, если на частицы среды действуют силы потенциального поля, а поперечные волны - при действии сил вихревого поля.

Геометрическое место точек, до которых в данный момент времени дошли колебания (волна), называется волновым фронтом (это поверхность, по одну сторону которой частицы среды колеблются, а по другую – еще нет.

Волновой поверхностью называется геометрическое место точек, в

которых частицы среды колеблются в одинаковой фазе или испытывают

одинаковые смещения. Волновой фронт и волновые поверхности всегда

перпендикулярны к направлению распространения волны .

Если волновой фронт и волновые поверхности являются плоскостями, то волна называется плоской, если сферами, то волна -

сферическая.

Длина волны - это расстояние между двумя соседними точками,

колеблющимися в одинаковой фазе (испытывающими одинаковое смещение).

Период колебаний T - это время, за которое волна со скоростью v

проходит путь :

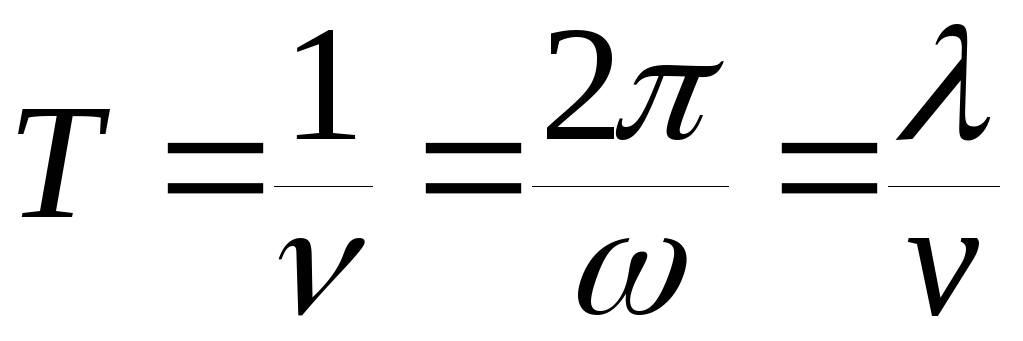, a величина

называется волновым числом.

Учитывая это, получаем выражение для волновой функции

плоской волны, распространяющейся вдоль оси x :

,

где - фаза волны, зависящая и от времени, и от координаты.

В точке с координатой x начальной фазой колебаний будет величина

. Волновая функция описывает колебания всех частиц среды в произвольный момент времени. Волны с одной фиксированной частотой и постоянной амплитудой называются монохроматическими . Для монохроматической волны волновая функция является бесконечной косинусоидой (или синусоидой), распространяющейся в

пространстве со скоростью . Такие волны называют бегущими.

2 Волновое уравнение. Скорость распространения волны

Любой процесс распространения волны в пространстве описывается одним и тем же дифференциальным уравнением – волновым уравнением :

.

Используя оператор Лапласа, волновое уравнение можно записать в

виде : . Решением волнового уравнения всегда будет вол -новая функция . Все результаты, полученные для монохроматической гармонической волны, будут справедливыми и для волн произвольной формы (сумма решений уравнения также является его решением). Поэтому далее будут исследоваться только монохроматические гармонические волны. Коэффициент, который стоит при производной в волновом уравнении, обязательно будет обратным квадратом скорости v волны. Это скорость перемещения волнового фронта и волновых поверхностей, т.е. точек, имеющих одинаковую фазу колебаний. Поэтому скорость v называют фазовой скоростью волны.

3 Электромагнитные волны

Рассмотрим электромагнитное поле в вакууме или в однородной диэлектрической среде, где нет свободных зарядов и токов проводимости : . Запишем для этого случая систему уравнений Максвелла :

(1) , (2) ,

(3) , (4) .

Выполнив ряд преобразований, получаем волновые уравнения

. .

В непроводящей среде электромагнитное поле существует в виде

электромагнитных волн - это колебания вихревых электрического и

магнитного полей, распространяющиеся со скоростью

.

Например, волновые функции для плоской электромагнитной волны

имеют вид

,.

Амплитуды электрического и магнитного полей в плоской электро - магнитной волне связаны соотношением

или .

Следовательно, в электромагнитной волне плотность энергии магнит –ного поля всегда равна плотности энергии электрического поля :

.

В любой электромагнитной волне векторы иколеблются в одинаковой фазе и образуют с вектором скорости волныправую тройку векторов.

4 Шкала электромагнитных волн

микро инфра ультра [Гц]

радио – волны красное фиолет. рентген.

вещание излучение излучение излучение

(тепло) видимый

телевидение спутниковое свет гамма -

TV излучение

радиоволны

Рис.1

Все излучения, показанные на диаграмме (рис.1), ( в том числе и видимый свет ) являются электромагнитными волнами, т.е. быстро - переменными колебаниями электрического и магнитного поля. Все

они распространяются с одной скоростью, скоростью света

, и отличаются только частотой колебаний и длиной волны.

Для видимого света 400 нм 780 нм или 3,7

.

Замечание : каждое из излучений, показанных на диаграмме

(рис.1), обладает свойствами волны (непрерывность, сплошной волновой фронт) и частицы (корпускулы) или фотона. Чем больше частота излучения, тем заметнее его корпускулярные свойства, и наоборот - чем частота меньше, тем сильнее проявляются волновые свойства. При малых частотах (радиоволны) практически проявляются только волновые свойства, а при больших частотах (  - излучение) его можно представить потоком частиц - фотонов.

5 Энергия и импульс электромагнитной волны

Электромагнитная волна - это электромагнитное поле в непроводящей среде. Вектор потока энергии, или вектор Пойнтинга для нее имеет вид , так как векторы образуют правую тройку векторов.

Поток энергии, переносимой электромагнитной волной, равен произведению плотности энергии электромагнитного поля на скорость распространения волны :

.

- это энергия, переносимая через единичную площадку за единицу времени.

Направление вектора Умова - Пойнтинга показывает направление переноса энергии волной, а его величина (энергия волны) всегда пропорциональна квадрату амплитуды колебаний.

Заметим, что амплитуда колебаний в сферической волне уменьшается обратно пропорционально расстоянию r от источника волны.

Импульс единицы объема электромагнитной волны равен

.

Tаким же импульсом обладает единица объема любого электромагнитного поля в любой среде.

Все электромагнитные волны отталкивают поглощающие или отражающие их тела, т.е. создают на них давление

.