Энергия магнитного поля

1 Энергия проводника с током

При изменении тока в замкнутой цепи в ней возникает самоиндукции.

Работа по перемещению заряда против этой э.д.с. идет

на изменение энергии тока.

-_c = L = L .

Пусть ток возрастает от 0 до , тогда в случае отсутствия ферромагнетикаи

Эта энергия W проводника с током индуктивностью L.

Работа источника сторонней э.д.с. идет и на изменение

внутренней энергии проводника, т.е. на выделение джоулева тепла

, и на изменение энергии тока в нем (в таком виде формула справедлива и в присутствии ферромагнетика):

W_ист=Q+.

Обычно проводники с токами взаимодействуют друг с другом.

Энергия системы двух замкнутых проводников с токами I₁ и I₂ имеет вид W = L₁I₁²/2 + L₂I₂²/2 + L₁₂I₁I₂ . Здесь величина (L₁I₁²/2 + L₂I₂²/2 ), которая всегда положительна, называется собственной энергией проводников с токами I₁ и I₂ , а величина L₁₂I₁I₂ - взаимной энергией токов, т.е. энергией их взаимодействия.

2 Энергия магнитного поля.

Рассмотрим бесконечно длинный соленоид с током I. Постоянное магнитное поле с индукцией / имеется только внутри соленоида, а энергия тока, текущего по участку соленоида длины , равна

,

где V - объем участка. Эта энергия будет одновременно энергией

магнитного поля, созданного таким током. Плотность энергии

магнитного поля, т.е. для энергии единицы объема:

.

Энергию магнитного поля, заключенного в произвольном объеме V , определяют по формуле : W = . Но эта формула справедлива, строго говоря, только для неферромагнитной среды !

Энергии контуров с токами не аддитивны.

Электрические колебания

1 Собственные электрические колебания

Электрический колебательный контур - это замкнутая электрическая цепь, обладающая некоторой емкостью C и индуктивностью L.

Если конденсатор емкости C первоначально был заряжен, то он начинает разряжаться, и в цепи возникает ток , вызывающий

появление э.д.с. самоиндукции _c, препятствующей изменению этого тока. В момент, когда конденсатор полностью разрядится, в цепи протекает ток I . Э.д.с. самоиндукции препятствует его мгновенному исчезновению, и он, постепенно затухая, начинает перезаряжать конденсатор. Затем конденсатор снова разряжается, ток течет в противоположном направлении и т.д. Электрические колебания

происходят за счет превращения электрической энергии заряженного конденсатора в магнитную энергию тока в цепи и наоборот.

Если к электрическому контуру не подключены никакие внешние источники переменной э.д.с., то колебания называются собственными.

Изменяться по периодическому закону будет величина заряда на конденсаторе, величины тока и напряжения в цепи.

Уравнение собственных затухающих колебаний имеет вид:

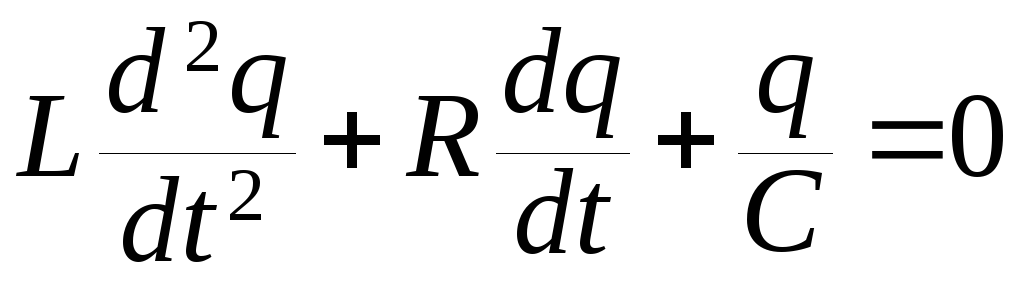или ,

где , .

Электрических колебаний в контуре не возникает, если его омическое

сопротивление R велико, или очень мала индуктивность L контура,

или слишком велика его емкость C, т.е. если выполнено условие

. Но если < , то e^{- t}. Собственные

электрические колебания в контуре происходят с частотой  (это частота собственных затухающих колебаний) :

и с уменьшающейся по экспоненциальному закону амплитудой e^-t . Причиной затухания колебаний в электрическом колебательном

контуре является превращение части энергии тока в джоулево тепло на

омическом сопротивлении R : dQ и рассеянии этого тепла в

окружающую среду.

Если сопротивление контура R пренебрежимо мало или отсутствует (для сверхпроводящего контура R=0 ), то колебания в контуре будут

незатухающими:

с частотой и с периодом .

2 Вынужденные электрические колебания

Подключим к электрическому колебательному контуру внешний источник э.д.с., изменяющейся по гармоническому закону с частотой_в.

Уравнение вынужденных гармонических колебаний: или .

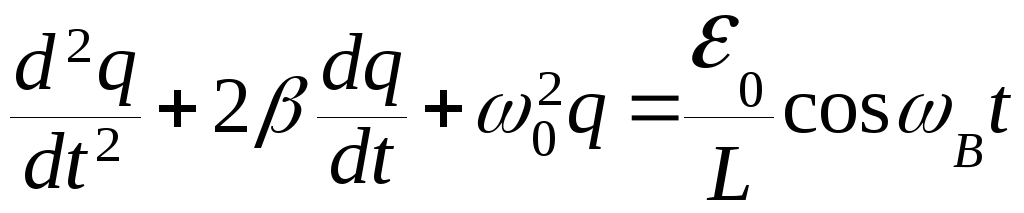Зависимость амплитуды A и начальной фазы вынужденных

колебаний заряда на конденсаторе от частоты вынуждающей э.д.с. и параметров контура:

и

(эти колебания происходят и в случае >).

Напряжение на конденсаторе при этом изменяется по закону

и отстает по фазе точно на от колебаний тока в контуре:

Если в цепь подключен источник постоянного напряжения U₀, то ток в цепи равен . Если же в цепь включен источник переменного напряжения , то амплитуды э.д.с. и тока в цепи связаны соотношением , где величина

называется полным сопротивлением или импедансом цепи. Составляющая R называется активным сопротивлением, а

- реактивным сопротивлением цепи.

Для переменного тока сопротивлением обладает как емкость, так и индуктивность. Величину называют емкостным сопротивлением , а- индуктивным сопротивлением.

Главное различие активного и реактивного сопротивления состоит

в том, что на активном сопротивлении R выделяется джоулево тепло,

а на реактивных сопротивлениях и- нет !

3 Резонанс. Характеристики электрического колебательного контура

Амплитуда вынужденных колебаний зависит от частоты внешнего источника э.д.с. График зависимости амплитуды от этой частоты называется амплитудно - частотной характеристикой контура.

При некоторой частоте внешнего источника амплитуда колебаний достигает максимума. Это явление называется резонансом, а

соответствующая частота - резонансной частотой .

Резонанс тока в контуре наступает при наименьшем значении

полного сопротивления , т.е. при или .

Резонансная частота для тока .

Резонанс напряжения на конденсаторе ищем из условия максимума 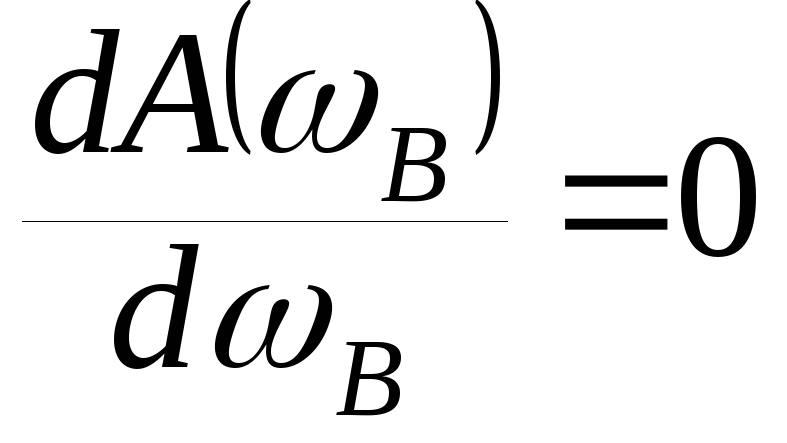. Резонансная частота для напряжения (заряда) на конденсаторе . При амплитуда напряжения на конденсаторе стремится к бесконечности ! Таким образом, даже если к контуру прикладывать малое внешнее

напряжение , то напряжение на отдельных элементах контура может быть очень большим ! В этом отношении резонансные явления опасны (пробой конденсатора, возникновение искры и т.п.).