4. Преобразования Лоренца

Преобразования Лоренца, связывают координаты и моменты времени одного и того же события в разных инерциальных системах отсчета (они аналогичны преобразованиям Галилея в классической теории).

Прямые Обратные

преобразования преобразования

Лоренца Лоренца

Особенности полученных выражений:

1) Прямые и обратные преобразования Лоренца связаны простой заменой v₀

на –v₀.

2) При эти преобразования переходят в преобразования Галилея:

x' = x - v₀t, y' = y, z' = z, t' = t. Иначе говоря, классическая механика является предельным случаем релятивистской (как того и требует принцип соответствия), если предположить возможность мгновенной передачи

взаимодействий на любые расстояния, т.е. с бесконечной скоростью c.

3) Преобразования имеют физический смысл только при v₀<c.

4) Такой простой вид преобразования имеют потому, что ось Ox направлена

по скорости движения системы K'.

5. Энергия релятивистской частицы

Полная энергия релятивистской частицы . Полная энергия включает в себя все виды энергии: механическую, тепловую, химическую, ядерную и т.д.

Энергия частицы при v=0, т.е. называетсяэнергией покоя. Это -- максимальная энергия, заключенная в покоящейся в данной системе отсчета частице (теле); она включает в себя энергию внутриатомных и внутриядерных взаимодействий.

Согласно определению, кинетическая энергия частицы (энергия движения) будет равна разности полной энергии и энергии покоя

Из формулы следует, что ни одна частица с массой, отличной от нуля, не может двигаться со световой скоростью ! И наоборот, безмассовые частицы (m=0) могут существовать, только двигаясь со скоростью света !

При малых скоростях (v << c)

и ,

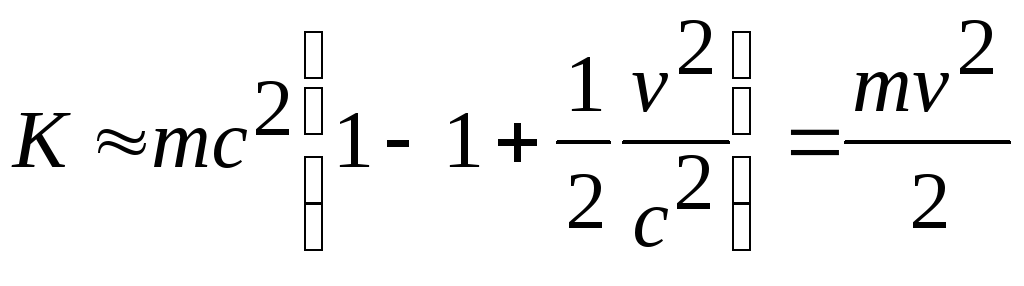т.е. формула приводит к хорошо известному классическому выражению

для кинетической энергии частицы.

С другой стороны, полную энергию можно представить, как сумму энергии покоя и кинетической энергии частицы .

Можно энергию и импульс объединить в один общий 4-вектор энергии--

импульса

или

Последнюю формулу можно применять и для безмассовых частиц, к которым относятся фотоны. Для них формула дает: E = pc.

Введение в термодинамику

1 Термодинамический и молекулярно-кинетический способы

описания

Термодинамической системой называется совокупность

макроскопических тел, состоящих из огромного числа независимо

движущихся молекул (материальных точек). Под телом может

подразумеваться и жидкость, и газ, и кристалл, и плазма и т.д.

Следовательно, термодинамическая система --- это система с огромным числом степеней свободы. Описать ее можно с помощью микроскопических параметров, т.е. скоростей, координат, масс отдельных молекул. Тогда изменение состояния системы, т.е. процесс, протекающий в ней, будет суммарным результатом движения всех молекул. Такой способ описания называется молекулярно--кинетическим или статистическим. Он используется в статистической физике.

Но можно описать термодинамическую систему, не интересуясь движением отдельных молекул, т.е. с помощью макроскопическихилитермодинамических параметров,характеризующих состояние системыв целом. Такими параметрами являются: объем V, давление p, температура T, поляризованность, намагниченностьи т.п. Этот способ описания называетсятермодинамическими изучается в термодинамике.

Если значения всех термодинамических параметров одинаковы во всех точках термодинамической системы и неизменны во времени, то она называется равновесной, а состояние такой системы - равновесным состоянием. Если же значения хотя бы одного термодинамического параметра различны в разных точках системы или он изменяется во времени,

то ее состояние называется неравновесным. Если любую физическую систему изолировать от внешних тел, то она приходит в равновесие: значения всех термодинамических параметров выравниваются во всех ее точках. Процесс перехода системы из неравновесного в равновесное состояние называется релаксацией, а время, за которое устанавливаются равновесные значения всех параметров системы, - временем релаксации .