2. Физический и математический маятники

Физический маятник -- это любое физическое тело, совершающее

колебания вокруг оси, не проходящей через центр масс, в поле сил тяжести.

Для того, чтобы собственные колебания системы были гармоническим, необходимо, чтобы амплитуда этих колебаний была мала. Кстати, то же справедливо и для пружинки: F_упр=-kx только для малых деформаций пружинки x.

Период колебаний определяется формулой:

.

Заметим, что квазиупругим здесь является момент силы тяжести

M_я = - mgd , пропорциональный угловому отклонению .

Частным случаем физического маятника является математический маятник -- точечная масса, подвешенная на невесомой нерастяжимой нити длины l. Период малых колебаний математического маятника

3. Затухающие гармонические колебания

В реальной ситуации на осциллятор со стороны окружающей среды всегда действуют диссипативные силы (вязкого трения, сопротивления среды)

, которые замедляют движение. Уравнение движения тогда принимает вид:

.

Обозначая и, получаем динамическое уравнение собственных затухающих гармонических колебаний:

.

Как и в случае незатухающих колебаний, это общая форма уравнения.

При не слишком большом сопротивлении среды <₀ колебания осциллятора совершаются по закону:

Функция представляет собою убывающую по экспоненте амплитуду колебаний. Это уменьшение амплитуды называетсярелаксацией (ослаблением) колебаний, а  называется коэффициентом затухания колебаний.

Время , за которое амплитуда колебаний уменьшается в e=2,71828 раз,

называется временем релаксации.

.

Кроме коэффициента затухания, вводится еще одна характеристика,

называемая логарифмическим декрементом затухания -- это натуральный

логарифм отношения амплитуд (или смещений) через период:

.

Частота собственных затухающих колебаний

зависит не только от величины квазиупругой силы и массы тела, но и от

сопротивления среды.

4. Сложение гармонических колебаний

Рассмотрим два случая такого сложения.

a) Осциллятор участвует в двух взаимно-перпендикулярных колебаниях.

В этом случае вдоль осей x и y действуют две квазиупругие силы. Тогда

Для того, чтобы найти траекторию осциллятора, следует исключить из этих уравнений время t.

Проще всего это сделать в случае кратных частот:

, где n и m -- целые числа.

В этом случае траекторией осциллятора будет некоторая замкнутая кривая, называемая фигурой Лиссажу.

Пример: частоты колебаний по x и y одинаковы (₁=₂=), а разность фаз колебаний (для простоты положим₁=0).

.

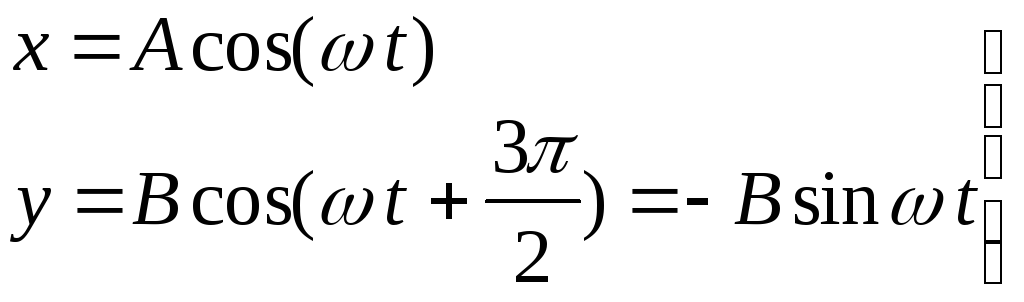Отсюда находим: -- фигурой Лиссажу будет эллипс.

б) Осциллятор совершает колебания одного направления.

Пусть таких колебаний пока будет два; тогда

где и-- фазы колебаний.

Аналитически колебания складывать очень неудобно, особенно, когда их

не два, а несколько; поэтому обычно используется геометрический метод векторных диаграмм.

5. Вынужденные колебания

Вынужденные колебания возникают при действии на осциллятор

внешней периодической силы, изменяющейся по гармоническому закону

с частотой _вн: .

Динамическое уравнение вынужденных колебаний:

Для установившегося режима колебаний решением уравнения будет гармоническая функция:

где A -- амплитуда вынужденных колебаний, а  -- отставание по фазе

от вынуждающей силы.

Амплитуда установившихся вынужденных колебаний:

Отставание по фазе установившихся вынужденных колебаний от внешней

вынуждающей силы:

.

\hs Итак: установившиеся вынужденные колебания происходят

с постоянной, не зависящей от времени амплитудой, т.е. не затухают,

несмотря на сопротивление среды. Это объясняется тем, что работа

внешней силы идет на

увеличение механической энергии осциллятора и полностью компенсирует

ее убывание, происходящее из-за действия диссипативной силы сопротивления

среды.