10. Регрессиялық талдау.
438~«Регрессия» терминін ... енгізген.
|Р. Фишер
|Ф. Гальтон
|К. Пирсон
|А. Кетле
|В. Уэлдон
439~Бір немесе бірнеше себептер және салдардың арасындағы байланысты өлшеуге мүмкіндік беретін статистикалық өңдеу әдісі – бұл ... талдау.
|дисперсиялық
|дискриминанталық
|регрессиялық
|корреляциялық
|статистикалық
440~Белгілері саны бойынша регрессияның бөлініуі:
|қарапайым, күрделі
|жұпталған, көпше
|әлсіз, күшті
|тура, кері
|тұрақты, айнымалы
441~Байланыстың бағыты бойынша регрессияның бөлініуі:
|жұпталған, көпше
|тура, кері
|қарапайым, күрделі
|әлсіз, күшті
|тұрақты, айнымалы
442~Егер нәтижелі белгі бір аргументтің функциясы ретінде қарастырылса, онда регрессия:
|дара
|көпше
|жұп
|қарапайым
|сызықты
443~Егер нәтижелі белгі бірнеше аргументтің функциясы ретінде қарастырылса, онда регрессия:
|көпше
|жұп
|дара
|қарапайым
|сызықты
444~Жұпталған регрессия теңдеуінің жалпы түрі:
|y=f(x1, x2,…, xn)
|y=ax+b
|y=f(x)
|y=a+b/x
|y= axb
445~Көпше регрессия теңдеуінің жалпы түрі:
|y=ax+b
|y=a+b/x
|y=f(x1, x2,…, xn)
|y= axb
|y=f(x)
446~Жұпталған регрессияның сызықты теңдеуі:
|y=eax+b
|у=a+bx
|y=a+b/x
|y=a+b1x+b2x2
|y=abx
447~Жұпталған регрессияның экспоненциалды теңдеуі:
|у=a+bx
|y=eax+b
|y=a+b/x
|y=a+b1x+b2x2
|y=abx
448~Жұпталған регрессияның гиперболалы теңдеуі:
|y=eax+b
|у=a+bx
|y=a+b1x+b2x2
|y=a+b/x
|y=abx
449~Жұпталған регрессияның параболалы теңдеуі:
|y=a+b1x+b2x2
|y=a+b/x
|y=eax+b
|у=a+bx
|y=abx
450~Жұпталған регрессияның көрсеткіштік теңдеуі:
|y=a+b1x+b2x2
|y=a+b/x
|y=abx
|y=eax+b
|у=a+bx
451~у=a+bx - жұпталған регрессияның ... теңдеуі.
|экспоненциалды
|гиперболалы
|сызықты
|параболалы
|көрсеткіштік
452~y=a+b1x+b2x2 - жұпталған регрессияның ... теңдеуі.
|сызықты
|параболалы
|экспоненциалды
|гиперболалы
|көрсеткіштік
453~y=a+b/x - жұпталған регрессияның ... теңдеуі.
|параболалы
|сызықты
|гиперболалы
|экспоненциалды
|көрсеткіштік
454~y=eax+b - жұпталған регрессияның ... теңдеуі.
|гиперболалы
|параболалы
|экспоненциалды
|сызықты
|көрсеткіштік
455~y=abx - жұпталған регрессияның ... теңдеуі.
|экспоненциалды
|көрсеткіштік
|гиперболалы
|параболалы
|сызықты
456~Регрессия теңдеуін құру, оның ... бағалауға алып келеді.
|нәтижелі белгіні
|факторлық белгіні
|коэффициенттерін
|тәуелді айнымалыны
|тәуелсіз айнымалыны
457~Регрессия теңдеуінің коэффициенттері ... әдісі арқылы анықталады.
|сенімділік аралық
|корреляциялық талдау
|ең кіші квадраттар
|статистикалық бақылау
|дисперсиялық талдау
458~ Ең кіші квадраттар әдісіннің маңызы:
|
|
|
|
|
459~Жұпталған регрессияның сызықты теңдеуінің еркін коэффициенттің анықтайтын формула:
|
|
|
|
|
460~Жұпталған регрессияның сызықты теңдеуінің коэффициенттерін анықтайтын формулалар:
|
,
|
,
|
,
| ,
|
,
461~Регрессия коэффициентінің статистикалық маңыздылығын бағалау үшін ... белгісі қолданылады.
|Фишер
|Стьюдент
|Пирсон
|Манн-Уитни
|Колмогоров-Смирнов
462~Стьюдент белгісіннің нөлдік болжамды тексеруде регрессия коэффициентінің маңыздылығының түрі:
|
|
|
|
|
463~Стьюдент белгісіннің баламалы болжамды тексеруде регрессия коэффициентінің маңыздылығының түрі:
|
|
|
|
|
464~Регрессия теңдеуінің маңыздылығын тексеру ... белгісі арқылы жүргізіледі.
|Пирсон
|Фишер
|Стьюдент
|Манн-Уитни
|Колмогоров-Смирнов
465~Регрессия теңдеуінің маңыздылығын тексеруде ... аңықталады.
|
|
|
|
|
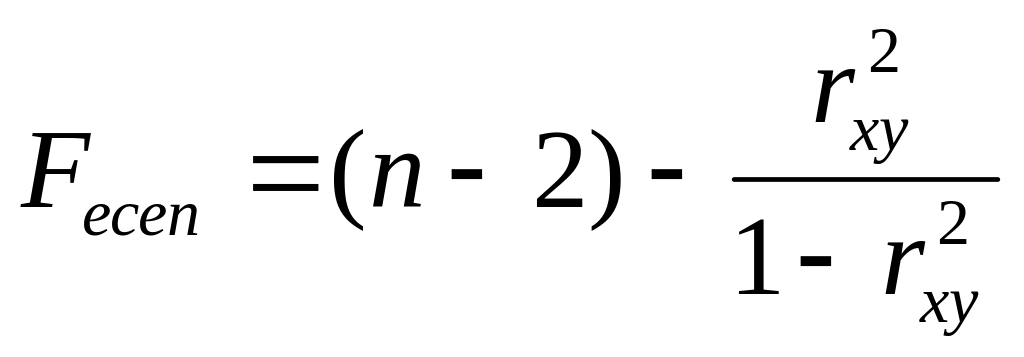
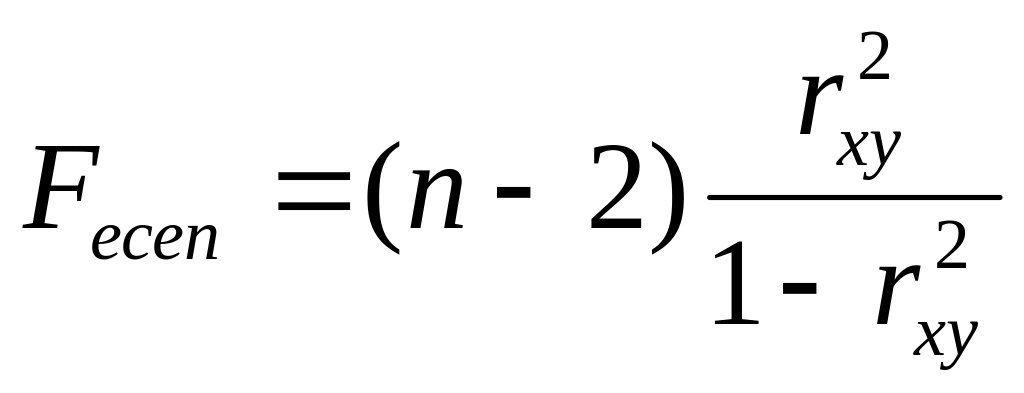
466~Детерминация коэффициенті ... аралығындағы мәндерді қабылдайды.
|[-1; 1]
|[0; 1]
|[-1; 0]
|[-10; 10]
|[1; 10]
467~... коэффициенті «у» белгісінің қандай бөлігі талдауда ескерілгендігін және талдауға енгізілген фактордын туғызатын әсерін көрсетеді.
|Корреляция
|Детерминация
|Вариация
|Ұқсас
|Түйіндес
468~Егер детерминация коэффициентті ... болса, регрессия теңдеуі сапалы болып табылады.
|≥0,8
|≤0,8
|≥0
|≤0
|=0