Электротехника и электроника для заочников / K00K07ER

Л Е К Ц И Я 7

1. Последовательная цепь синусоидального тока с резистивным,

емкостным и индуктивным элементами.

2. Фазовые соотношения между током и напряжением.

3. Резонанс напряжений.

Рассмотрим цепь с последовательным соединением и (рис.14).На зажимы А и Д подано синусоидальное напряжение.

Рис.14

Согласно 2-му закону Кирхгофа в комплексной форме справедливо уравнение: где Или

которое удобно представить в виде

где - активное сопротивление (всегда положительно),

- реактивное сопротивление.

Тогда

При знаке "+" цепь носит индуктивный характер, при знаке "-" - емкостной характер.

Запишем комплексное сопротивление в показательной форме

где

- полное сопротивление, модуль комплексного сопротивления,

- аргумент комплексного сопротивления

Угол - угол сдвига фаз между напряжением и током.

В справедливости вышеприведенных выражений легко убедиться, если изобразить комплексное число вектором на комплексной плоскости.

Треугольник, образованный векторами и , называется треугольником сопротивлений. Удобно пользоваться следующими выражениями: ;

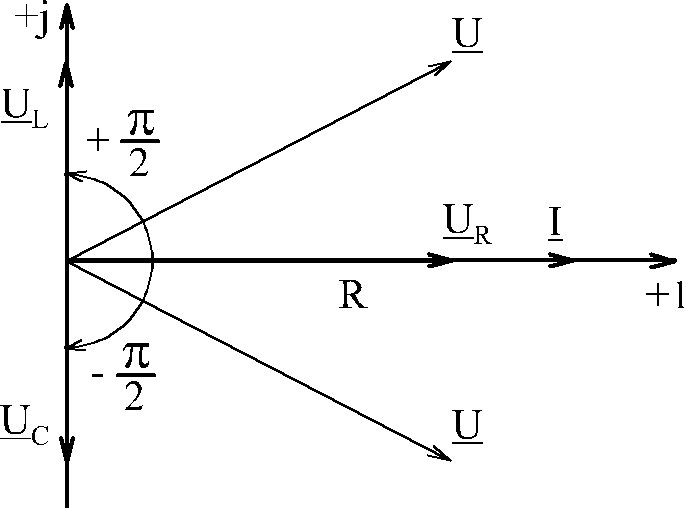
2. Фазовые соотношения между током и напряжением.

Положительный угол (при индуктивной или активно-индуктивной нагрузке) откладывают от вектора тока против часовой стрелки, отрицательный угол (при емкостной или активно-емкостной нагрузке) - по часовой стрелке (рис.15).

Рис. 15

На рис.16 построены векторные диаграммы для последовательной цепи

а) в случае

б) с случае

в) в случае

Рис.16

Мощность цепи переменного тока имеет три составляющие: реактивные - индуктивную и емкостную мощности и активную мощность .

Рассмотрим связь между полной мощностью и ее составляющими.

Для последовательной цепи в треугольнике сопротивлений умножаем все стороны треугольника на . Получим треугольник напряжений (рис.17,b).

Если умножить все стороны треугольника сопротивлений на I , получаем треугольник мощностей (рис.17,в). В нем

Рис.17

Как и любую электрическую величину мощность также можно представить в виде комплексного числа (алгебраическая форма):

Для получения комплекса мощности следует взять произведение комплекса напряжений на сопряженный комплекс тока:

Тригонометрическая форма комплексной мощности:

3. Резонанс напряжений.

При последовательном соединении элементов с и (рис.14) ток в цепи

Наиболее важный момент в такой цепи является случай, когда .

Тогда реактивное сопротивление цепи , а полное сопротивление минимально. В этом случае ток в цепи при и его значение минимально.

Напряжения на индуктивном и емкостном элементах в комплексной форме , а по значению

Следовательно

Таким образом, напряжения и могут превышать напряжения сети в раз, если . Сдвиг по фазе между напряжениями и равен ,

т.е. эти напряжения находятся в противофазе.

Такой режим цепи при последовательном соединении элементов с и когда , а напряжения и элементов находятся в противофазе, равны по значению и могут превышать напряжение всей цепи, носит название режим резонанса напряжений.

На рис.18 представлена векторная диаграмма для режима резонанса

напряжений.

Активная мощность такой цепи а реактивная . Но реактивная мощность индуктивного и емкостного элементов не равны нулю: .

Рис.18

Явление резонанса широко используется в технике: в устройствах радиотехники, телевидения, автоматики и других электроустройств. Изменяя индуктивность или емкость , можно настраивать контур на ту или иную резонансную частоту и усиливать в цепи ток той или иной частоты.

В некоторых случаях необходимо учитывать при резонансе напряжений увеличения напряжения и тока, что может привести к пробою изоляции элементов цепи.