§3. Уравнение касательной и нормали к графику функции.

Пусть кривая есть график функции у= (х). М (х₀, у₀) – произвольная точка на ней, в точке существует касательная.

Рис.5.

Определение: нормалью к кривой у= (х) в точке М₀называется прямая, проходящая через точку М₀и перпендикулярна касательной в точке М₀к этой кривой.

Напишем уравнение касательной и нормали, зная уравнение кривой и координаты точки М₀. Касательная имеет угловой коэффициент к= t_g=^,(х₀). Из аналитической геометрии известно, что прямая имеет уравнение у- у₀= к( х – х₀).

Поэтому уравнение касательной: у - у₀=^,(х₀)(х – х₀); (1)

Угловой коэффициент нормали К_н=(так как они перпендикулярны), но тогда уравнение нормали:

у- у₀=(-1/^,(х₀)( х – х₀); (2)

Если в точке не существует производная, то в этой точке не существует и касательная.

Например, функция (х)=|х| в точке х=0 не имеет производной.

lim_х_0(_у/_х)= lim_х_0(|_х|/_х)=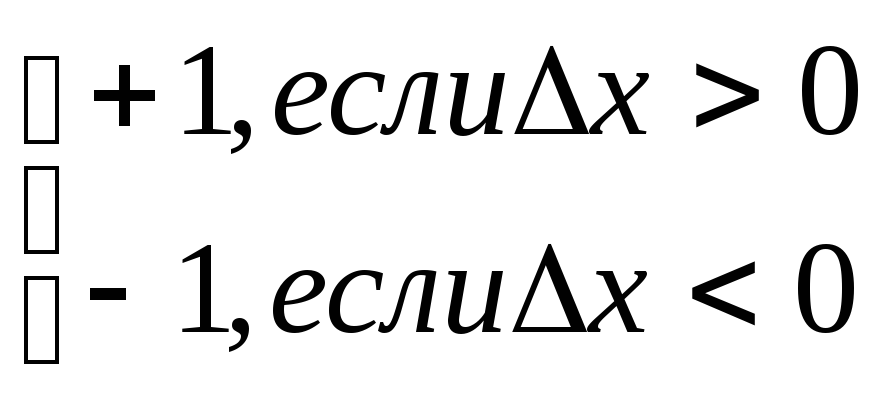

Односторонние пределы существуют, но lim_х_0(_у/_х) не существует

y

y=|x|

Рис.6 x

Касательная тоже.

Такая точка называется угловой точкой графика.

§4. Связь между непрерывностью и дифференцируемостью функции.

Справедлива следующая теорема о дифференцируемой функции.

Теорема: если функция у= (х) имеет конечную производную в точке х_0, то функция непрерывна в этой точке.

Доказательство:

Т.к. в точке х₀существует производная^,(х₀), т.е. существует предел

lim_х_0(_у/_х)=^,(х₀), то_у/_х=^,(х₀)+, где

- б.м.в., зависящая от _х. При_х0,0, т.к.= (_у/_х) -^,(х₀)0 при_х0

Отсюда имеем: _у=^,(х₀) _х +_х.

Но тогда

Бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, поэтому (х) непрерывна в точке х₀.

Важно понять, что обратная теорема не верна!

Не всякая непрерывная функция является дифференцируемой.

Так, (х) =хявляется непрерывной в точке х₀=0, график – сплошная линия, но^,(0) не существует.

§5. Производные постоянной, синуса, косинуса и степенной функции.

1. у= (х) =с; у^,= (с)^,= 0; (1)

Доказательство:

а) в любой точке х (х) = с

б) дадим х приращение _х, х +_х, значение функции(х +_х)= с;

в) (х +_х)-(х)= с- с= 0;

г) _у/_х= 0/_х = 0

д) lim_х_{0 (}у/_х)= lim_х_00 = 0

2. у= sin х; у^,= (sin х)^,= cos х; (2)

Доказательство:

а) в любой точке х (х) = sin х;

б) дадим х приращение _х, х +_х, значение функции

 (х +_х)= sin (х +_х);

в) _у = sin (х +_х) - sin х = 2 sin (_х/ 2)cos (х + (_х/ 2));

г) _у/_х = ((sin (_х/ 2)) / (_х/ 2))cos (х + (_х/ 2));

lim_х_0 ((sin (_х/ 2)) / (_х/ 2))cos (х + (_х/ 2))= 1 lim_х_0(cos (х + (_х/ 2))= cos х (т.к.cosx– непрерывная функция).

1. Аналогично у= cos х, у^,= (cos х)^,= - sin х; (3)

2. у= хⁿ,n-целое положительное, у^,= (хⁿ)^,=nх^n-1,(4)

(Позднее формула будет доказана для любого n, не обязательно натурального).