§8 Касательная плоскость и нормаль к поверхности. Геометрический смыл полного дифференциала функции двух переменных.

Предварительно вспомним известные и выведем новые формулы для касательных и нормалей к плоским и пространственным кривым.

На плоскости:

Если кривая задана явной функцией y=f(x), то, как мы знаем, уравнение касательной к ней в точке (x₀,y₀) имеет вид: , а уравнение нормали:.

Если кривая есть график функции, заданной неявно уравнением F(x,y)=0, то, как было показано, и потому уравнение касательной будет. Уравнение нормали:.

Если кривая задана параметрически: то уравнение касательной имеет вид:, уравнение нормали:.

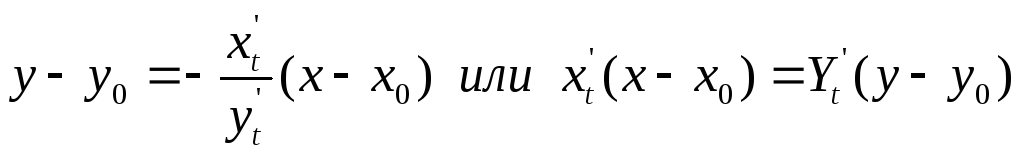В пространстве наиболее употребительно задание кривой в параметрической форме: Пусть дана точка Р₀ (x₀,y₀,z₀) на этой кривой, она соответствует параметру t₀.

Рассмотрим приращенную точку Р(x₀+x, y₀+y, z₀+z) этой кривой, она соответствует значению параметра t₀+t. Проведем секущую через точки Р₀ и Р. Из аналитической геометрии известно, что уравнение этой секущей по двум точкам будет иметь вид . Разделим все знаменатели наt и перейдем к пределу при. Тогда секущая стремится к предельному положению –касательной и ее уравнение будет соответственно . Так как , ,есть в этом уравнении координаты направляющего вектора касательной, то направляющие векторы касательной будутcos, cos cos. Если рассмотрим теперь дифференциалы ,,, то видим пропорциональность этих дифференциалов направляющим косинусам касательной

^число

Перейдем теперь к рассмотрению касательной плоскости и нормали к поверхности. Пусть поверхность задана уравнением F(x, y, z)=0 иP₀(x₀, y_0, z₀) - точка на ней. Проведем на поверхности произвольную кривую L через точку P₀. В параметрическом виде уравнение этой кривой будет 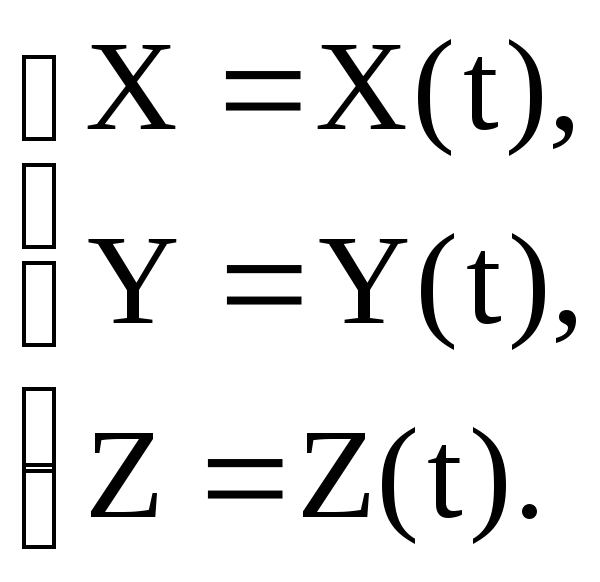Так как кривая лежит на поверхности, то уравнения кривой должны удовлетворять уравнению поверхности: F. Возьмем полный дифференциал от обеих частей. В силу инвариантности формы дифференциала можно записать(1) или, заменяя дифференциалы на пропорциональные косинусы, перепишем(2) (скалярное произведение в координатной форме). Равенство (2) можно рассматривать как условие перпендикулярности двух прямых. Одна из них является касательной к кривойL в точке P₀, - ее направляющие косинусы. Тогда величины - есть величины, пропорциональные направляющим косинусам нормали к кривой L в точке P₀. Но эти производные есть числа (они вычисляются в точке P₀), поэтому они не зависят от кривой L и, значит, для любой кривой L, проходящей через точку P₀ на поверхности, будут одними и теми же.

Но последнее означает, что нормаль ко всем касательным в точке P₀ будет одна и та же, а это означает, что все касательные ко всевозможным кривым в точке P₀ лежат в одной плоскости. Эта плоскость - геометрическое место всех возможных касательных - и называется касательной плоскостью к поверхности в точке P₀. А прямая, перпендикулярная касательной плоскости, называется нормалью к поверхности в точке P₀. Вообще, уравнение любой плоскости, проходящей через точку P_0, есть A(x-x₀)+ B(y-y₀)+ C(z-z₀) = 0, где А,В,С величины пропорциональные направляющим косинусам нормали. Величины ,,- пропорциональны направляющим косинусам нормали, поэтому++=0 (3) - уравнение касательной плоскости. Уравнение нормали запишется, очевидно, в виде(4). Все производные,,есть числа, вычисляются в точкеP₀ (x₀ ,y₀, z₀).

Если поверхность задана явным уравнением z = f(x,y), то его можно переписать в виде f(x,y) – z = 0. Отсюда ++=0 (,() - уравнения касательной плоскости и нормали к поверхности, заданной в явном виде.

Выясним теперь геометрический смысл полного дифференциала функции z = f(x,y). Из уравнения касательной плоскости (имеем+. Можем считать, что,, тогда. Но справа стоит полный дифференциал функции z = f(x,y), потомуdx. Это равенство и позволяет выяснить геометрический смысл полного дифференциала dz.

Пусть в точке P₀ (x₀ ,y₀, z₀) проведена касательная плоскость. Передвигаясь по поверхности, перейдем в точку P (x₀+,y₀+, z₀+) этой поверхности. В точке P₀ аппликата z₀=AP₀. В точке P аппликата z=BP. Пусть AP₀=BC. Тогда CP=.

Если же из точки P₀ по касательной плоскости перейдем в точку D, CD = z – z₀; но dx. Таким образом, полный дифференциал dz функции z = f(x,y) в точке (x₀,y₀) совпадет с приращением аппликаты точки на касательной плоскости к поверхности z = f(x,y) в точке P₀ (x₀ ,y₀, z₀). Из чертежа видно, что чем меньше и, тем меньшеотличается от, что оправдывает равенство.