
- •§1. Понятие ф.Н.П., ее области определения. Геометрическое
- •§2 Предел и непрерывность функции нескольких переменных.
- •§3 Частные производные функции нескольких переменных.
- •§4 Полное приращение и полный дифференциал ф.Н.П. Дифференцируемость ф.Н.П.
- •§5 Производные сложных функций нескольких переменных. Полная производная.
- •Заметим, что для большего числа переменных формулы (1)-(3) естественным образом обобщаются. Если и,, ... ,, то
- •§6 Инвариантность формы полного дифференциала ф.Н.П.
- •§7 Производная от функции, заданной неявно.
- •§8 Касательная плоскость и нормаль к поверхности. Геометрический смыл полного дифференциала функции двух переменных.
- •§9 Частные производные высших порядков.
§7 Производная от функции, заданной неявно.
Сначала
рассмотрим неявную функцию одного
переменного. Она определяется уравнением
![]() (1), которое каждому х из некоторой
области Х сопоставляет определённое
у. Тогда на Х определяется этим уравнением
функция у=f(х).
Её называют неявной
или неявно
заданной.
Если уравнение (1) удаётся разрешить
относительно у, т.е. получить вид у=f(х),
то задание неявной функции становится
явным. Однако
разрешить уравнение удается не всегда
и в этом случае не всегда ясно –
существует ли вообще неявная функция
у=f(х),
определяемая уравнением (1) в некоторой
окрестности точки ( x0,
y0
).
(1), которое каждому х из некоторой
области Х сопоставляет определённое
у. Тогда на Х определяется этим уравнением
функция у=f(х).
Её называют неявной
или неявно
заданной.
Если уравнение (1) удаётся разрешить
относительно у, т.е. получить вид у=f(х),
то задание неявной функции становится
явным. Однако
разрешить уравнение удается не всегда
и в этом случае не всегда ясно –
существует ли вообще неявная функция
у=f(х),
определяемая уравнением (1) в некоторой
окрестности точки ( x0,
y0
).
Например,
уравнение
![]() неразрешимо относительноy
и неясно - определяет ли оно неявную
функцию в некоторой окрестности точки
(1,0), например. Заметим, что существуют
уравнения, не определяющие никакой
функции (x2+y2+1=0).
неразрешимо относительноy
и неясно - определяет ли оно неявную
функцию в некоторой окрестности точки
(1,0), например. Заметим, что существуют
уравнения, не определяющие никакой
функции (x2+y2+1=0).
Оказывается справедливой следующая теорема:
Теорема«Существования и дифференцируемости неявной функции» (без доказательства)
Пусть
дано уравнение
![]() (1) и функция
(1) и функция![]() ,
удовлетворяет условиям:
,
удовлетворяет условиям:
Сама функция
 и
ее частные производные
и
ее частные производные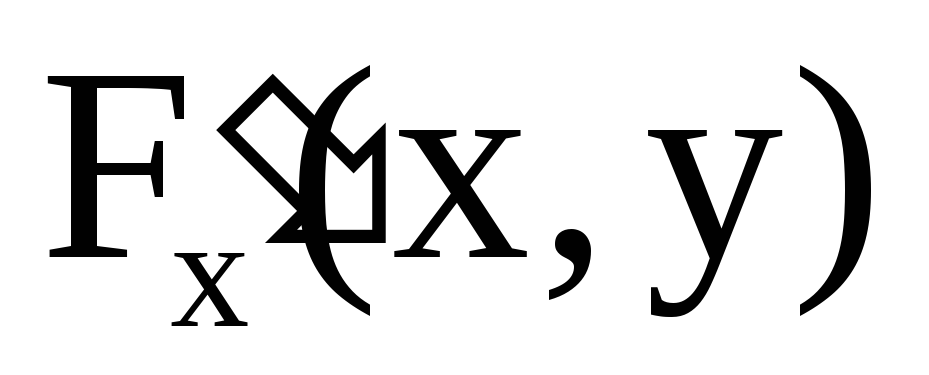 и
и непрерывны в некоторой окрестности
точки М0
(х0,у0);
непрерывны в некоторой окрестности
точки М0
(х0,у0); ;
; .
.
Тогда:
уравнение (1) при значении х близких к х0 определяет однозначную неявную функцию у=f(х);
 ;
;эта функция непрерывна в окрестности точки х0;
она имеет непрерывную производную в этой окрестности, вычисляющуюся по формуле:
![]() .
(2)
.
(2)
Геометрически
теорема утверждает, что в окрестности
точки
![]() ,
где выполняемы условия теоремы, неявная
функция, определяемая уравнением (1),
может быть задана в явном виде у=f(х),
т.к. каждому значению х соответствует
единственное у. Если даже мы не можем
найти выражение функции в явном виде,
мы уверены, что в некоторой окрестности
точки М0
это уже
возможно в принципе.
,
где выполняемы условия теоремы, неявная
функция, определяемая уравнением (1),
может быть задана в явном виде у=f(х),
т.к. каждому значению х соответствует
единственное у. Если даже мы не можем
найти выражение функции в явном виде,
мы уверены, что в некоторой окрестности
точки М0
это уже
возможно в принципе.
Рассмотрим
тот же пример:
![]() .
Проверим условия:
.
Проверим условия:
1 )
)![]() ,
,![]() - и функция и её производные непрерывны
в окрестности точки (1,0) (как сумма и
произведение непрерывных).
- и функция и её производные непрерывны
в окрестности точки (1,0) (как сумма и
произведение непрерывных).
2)
![]() .
.
3)
![]() .
Значит, неявная функция у=f(х)
существует в окрестности точки (1,0). Мы
не можем её выписать в явном виде, но
можем все-таки найти её производную,
которая будет даже непрерывной:
.
Значит, неявная функция у=f(х)
существует в окрестности точки (1,0). Мы
не можем её выписать в явном виде, но
можем все-таки найти её производную,
которая будет даже непрерывной:

Рассмотрим теперь неявную функцию от нескольких переменных. Пусть задано уравнение
![]() . (2)
. (2)
Если
каждой паре значений (х,у) из некоторой
области уравнение (2) сопоставляет одно
определённое значение z,
то говорят, что это уравнение неявно
определяет однозначную функцию от двух
переменных
![]() .
.
Справедлива и соответствующая теорема существования и дифференцирования неявной функции нескольких переменных.
Теорема
2: Пусть дано
уравнение
![]() (2) и функция
(2) и функция![]() удовлетворяет условиям:
удовлетворяет условиям:
 ,
,
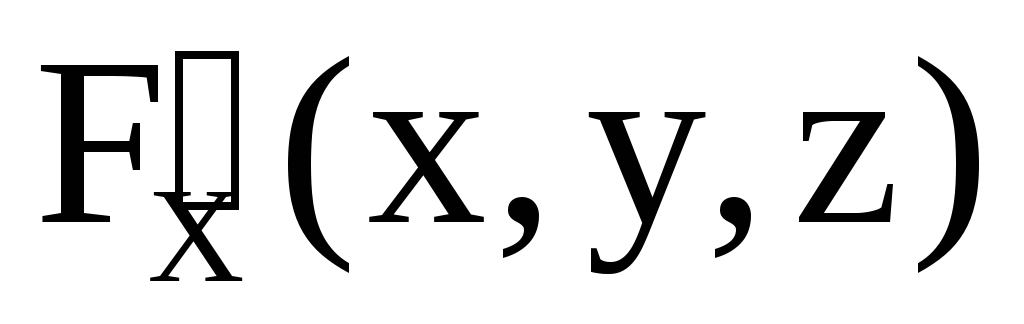 ,
, ,
, -
существуют и непрерывны в некоторой
окрестности точки
-
существуют и непрерывны в некоторой
окрестности точки ;
;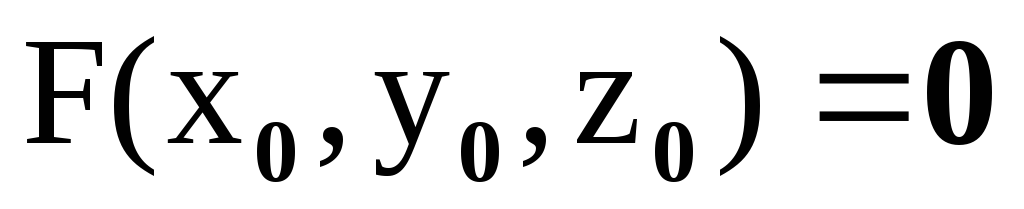 ;
;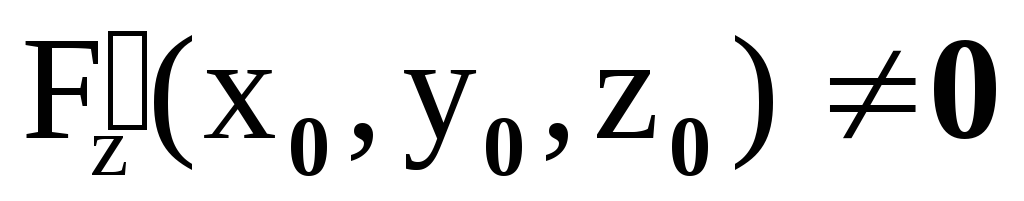 .
.
Тогда:
в некоторой окрестности точки М0 уравнение (2) определяет z как однозначную функцию от х,у:
 ;
; ;
;функция
 непрерывна в этой окрестности;
непрерывна в этой окрестности;неявная функция
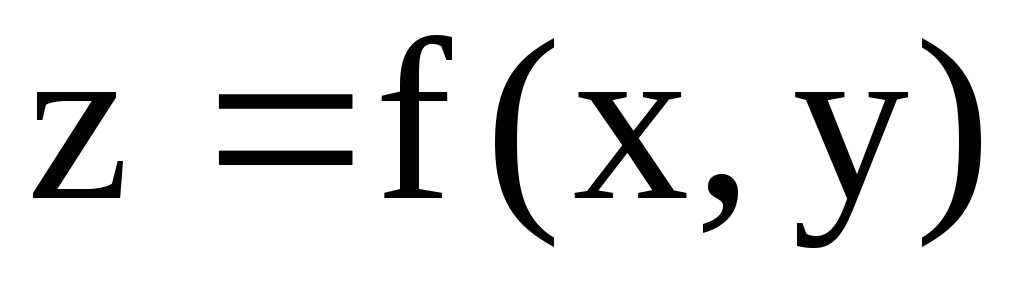 имеет непрерывные частные производные
в этой окрестности, вычисляемые по
формулам:
имеет непрерывные частные производные
в этой окрестности, вычисляемые по
формулам:
 .
.
Пример:
![]() .
Это уравнение задаётz
как двузначную неявную функцию от х и
у
.
Это уравнение задаётz
как двузначную неявную функцию от х и
у
![]() .
Если проверить условия теоремы в
окрестности точки, например, (0,0,1), то
видим выполнение всех условий:
.
Если проверить условия теоремы в
окрестности точки, например, (0,0,1), то
видим выполнение всех условий:

 -
непрерывна,
-
непрерывна,
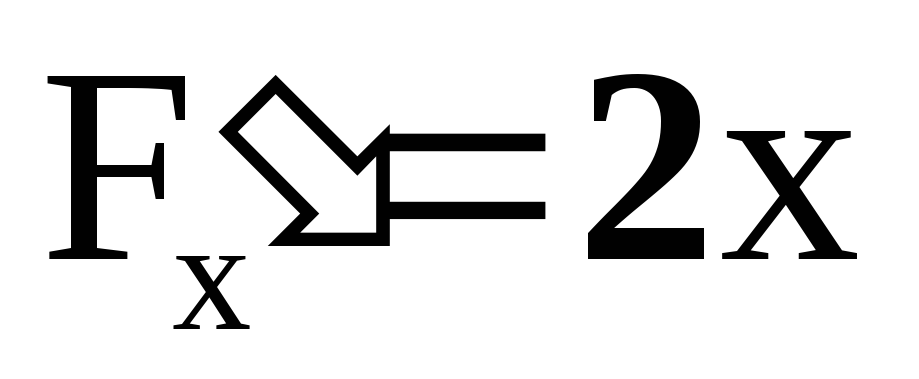 ,
,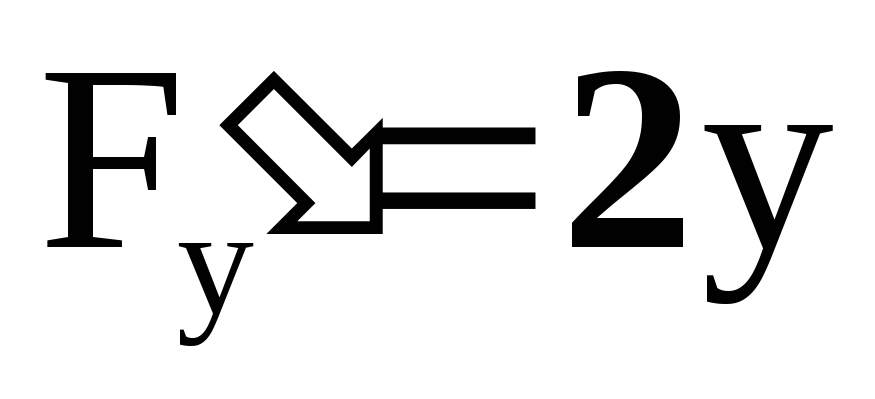 ,
,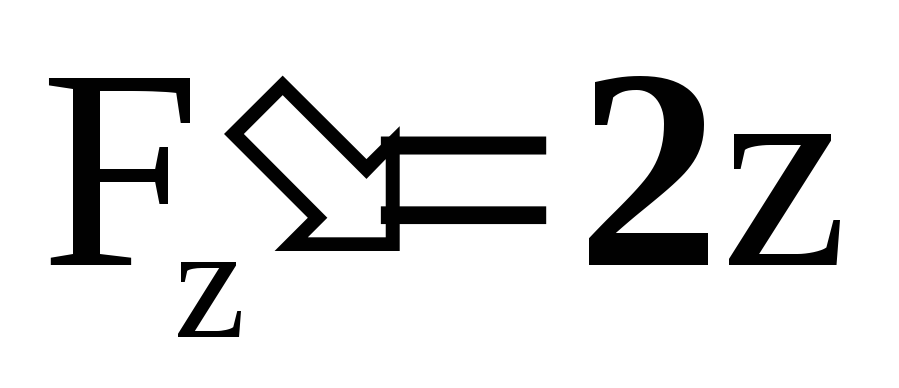 -
непрерывны также;
-
непрерывны также;F(0,0,1)=1-1=0;
 .
.
Значит,
неявная однозначная функция существует
в окрестности точки (0,0,1): Можно сказать
сразу, что это
![]() ,
задающая верхнюю полусферу.
,
задающая верхнюю полусферу.
Существуют
непрерывные частные производные
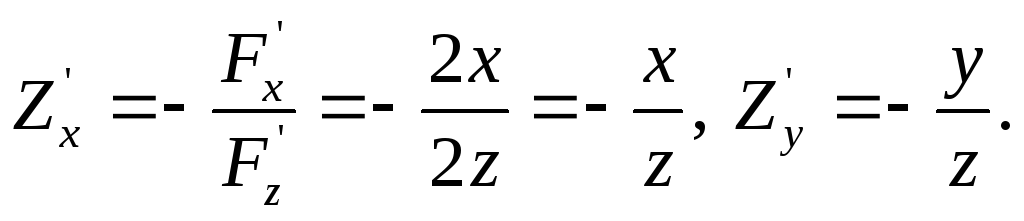 Они, кстати, получаются такими же, если
дифференцировать неявную функцию,
выраженную в явном виде, непосредственно.
Они, кстати, получаются такими же, если
дифференцировать неявную функцию,
выраженную в явном виде, непосредственно.
Определение и теорема существования и дифференцирования неявной функции большего числа аргументов аналогичны.
