§2.Кривизна плоской кривой. Ее вычисление

Рассмотрим произвольную непрерывную кривую АВ., которая не имеет точек самопересечения. Если в каждой ее точке М провести касательную, то она при перемещении т.М от А к В будет поворачиваться.

Этим кривая отличается от прямой, где касательная всегда направлена одинаково, а именно: сливается с прямой.

Чем быстрее поворачивается касательная, тем больше искривлена кривая линия, тем больше ее "кривизна".

Дадим математическое определение кривизны кривой. Рассмотрим произвольную дугу ММ1, в точках М и М1 проведем касательные. Пусть угол между ними , он назыв углом смежности, дугаММ1=S. Тогда отношение /S назыв. средней кривизной кривой АВ на участке ММ1. Средняя кривизна показывает величину угла поворота касательной при перемещении точки М на единицу длины по кривой. На разных участках кривой средняя кривизна меняется. Лишь для одной кривой - окружности средняя кривизна постоянна: к_ср=/S=/(R)=1/R, те для окружности кривизна есть величина обратная радиусу.

Для точной характеристики искривленности кривой вводят понятие кривизны в точке, обозначают К.

Определение:

Кривизной кривой в т.М назыв предел (если он сещ-ет), к которому стремится сред кривизна дуги ММ1, когда т.М1 по кривой стремится к М.

К=lim_S/s, (1). Для окружности К=1/R.

Предел (1) есть не что иное как производная угла наклона касательной по длине дуги, а потому последний предел есть предел отношения приращения функции к приращ аргумента, т.е. производная: К=d/dS, (2).

Таким образом, кривизна кривой в точке есть производная угла наклона касательной по длине дуги кривой. Кривизна есть число неотрицательное, поэтому на самом деле К=| d/dS|, (2').

Из ф-лы (2) кривизны получим удобную на практике ф-лу, когда кривая задается параметрически.

Предполагаем дополнительно, что функции (t) ,(t) имеют непрерывные производные 1и 2 порядков и xt'='(t) при t соответствующем т.М.

Тогда dS=, определимd.

tg=у_х'=у_t'/х_t', отсюда =arctg у_t'/х_t',

d=, подставляя dS, d в (2') получим К=||, (3).

Если кривая задана явным уравнением у=f(х) считаем параметр t=х, тогда и К=||, (4).

Если кривая задана полярным уравнением , то считая t= получим подставляя в (3) получим К=||, (5)

Пример. Определить кривизну кривой у=sinх в т.х=П/2 -САМОСТОЯТЕЛЬНО.

Ответ: K=1.

§3.Радиус, круг и центр кривизны. Понятие эволюты и эвольвенты.

Определение: величина R, обратная кривизне кривой К в точке, назыв радиусом кривизны кривой в этой точке: R=1/К. Для прямой радиус кривизны равен бескон-ти, те прямая -это окружность бесконечного радиуса.

Для окружности радус кривизны- это ее обычный радиус, Для кривых, заданных в параметрической форме или явными уравнениями у=f(х) или  радиус кривизны находится по формулам легко получаемых из (3)-(5). Так для у=f(х) R=1/К=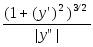, и т.п.(самим).

Построим в т.М кривой нормаль к ней и отложим в сторону вогнутости отрезок МС=R.

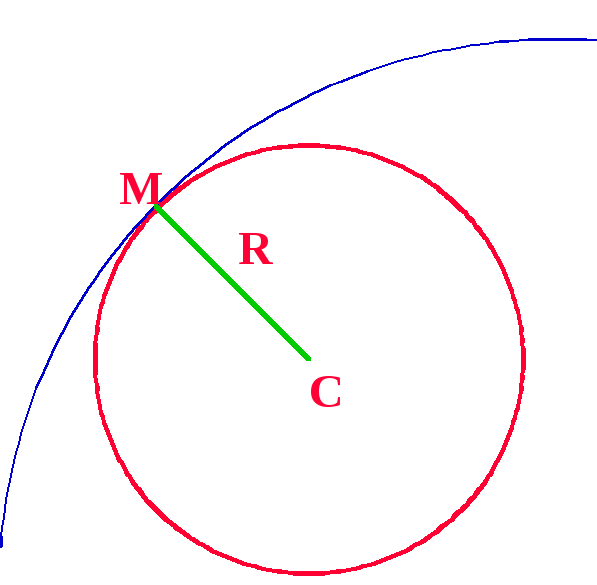
Точка С назыв центром кривизны в данной т.М, круг (окружность) с центром С и радиусом R назыв кругом (окружностью) кривизны линии в т.М. В т.М кривая и окружность кривизны им одинаковую кривизну К, поэтому дугу кривой вблизи М с малой ошибкой можно заменять дугой окружности кривизны в этой точке.

Каждой точке М кривой (L) соответствует своя точка С- центр кривизны в т.М.

Геометрическое место центров кривизны кривой (L) называется ее эволютой (L'). (L')-есть тоже некоторая кривая. По отношению к (L') исходная кривая (L) называется эвольвентой или разверткой. Существуют формулы , позволяющие по данному уравнению кривой (L) написать уравнение эволюты. И наоборот.

Практически эволюту по данной кривой можно построить так. Можно доказать, что каждая нормаль к кривой (L) явл. касательной к эволюте. Поэтому построив достаточное кол-во нормалей проводим к ним кривую, которая касается всех этих нормалей- огибающую семейства нормалей.

Эвольвенту по эволюте можно построить механическим способом.

Пусть гибкая линейка согнута по виду эволюты С₀С. Прикрепим к концу С₀ нить и туго натянем на линейку.

C

эволюта

C0

эвольвента

Если теперь эту нить развертывать, натягивая ее все время за свободный конец, то он опишет кривую, которая будет эвольвентой кривой С₀С. Т.к. нити могут иметь разную длину, то эвольвент у одной эволюты может быть сколько угодно.

174