§4. Вычисление поверхности тела вращения.

Если вращать кривую АВ:около осиOX, B

то получим поверхность (S) — поверхность вращения.Как A

найти площадьS этой поверхности ? Разобьём на

элементарные точками.

Проведём через них поперечные сечения. Они разобьют

тело на слоёв. Заменим каждый слой усечённым конусом с теми же основаниями и той же высотой. Радиусы оснований будути, длина образующей.Тогда боковая поверхность- го конуса будет:, и поверхность ступенчатой фигуры

.

Переходя к пределу при, получим площадь поверхности (S):

, итак,

Пример. Вычислить поверхность сферы радиуса .

Решение. Сфера получается вращением полуокружности около осиOX. Поэтому имеем: и

§5. Некоторые механические приложения определённого интеграла.

1. Вычисление работы силы.

Пусть материальная точка под действием силыперемещается по прямой из точки в точку.направлена в сторону движения. Возможны два случая:

а) силапостоянна по величине. Тогда работа силы

(сила на путь);

b) сила изменяется по величине с изменением абсциссыточки, т.е.— функция от. Будем предполагать, чтонепрерывна на.Разобьёмнаэлементарных участков с длинами. На каждом из них выберем по одной произвольной точкеи будем считать, что насила везде одинакова и равна. Тогда работа на- ом участке будет:и.

Это приближённое равенство будет тем точнее, чем мельче разбиение на части. Точное равенство получится при. Но справа стоит интегральная сумма для непрерывной функции, а потому предел существует, и есть определённый интеграл. Таким образом, работа

переменной силы нанаходится по формуле:

Пример. Какую работу нужно совершить, чтобы тело массы поднять с поверхности Земли на высоту?

Решение. Пусть — радиус Земли,- масса Земли. Сила, действующая на тело массыравна, где— расстояние от центра Земли до тела. Так как приимеем,

то , поэтому. Исполняемая работа:

.

2)Вычисление статических моментов и центра масс дуги плоской кривой.

Сначала определим понятие статических моментов и центра масс

системы изолированных точек.

Пусть имеется несколько материальных точек на плоскости

(аналогично и в пространстве) , в которых C

cосредоточены массы и пустьсуммарная 0

масса всей системы. Статическим моментом материальной точки относительно осиназывается величина, относительно осивеличина. Статическим моментом системы материальных точек относительно осейисоответственно являются суммы:.

Определение. Центром масс системы материальных точек называют такую точку , что если в ней сосредоточить всю массу системы, то её статический момент относительно каждой оси равен статическому моменту всей системы относительно этой оси, т.е..

Тогдакоординаты центра масс будут:

Пусть теперь имеем материальную кривуюс линейной плотностью

материала. Сама кривая задана параметрическими уравнениями: B

, , причём насами функции и ихA

производныеинепрерывны, функцию плотности 0

тоже предполагаем непрерывной. Разобьём на

элементарные части точками .

Соответствующие этимточкиразобьютна элементарные дуги. Будем обозначать длины их.Так как размерымалы, то распределение массы по ней можно считать равномерным и равным, например,.Тогда, и(1).

Статические моменты кривой относительно осей будут:

(2), (3).

Чем мельче дробление , тем мельче дробление, тем точнее эти неравенства. Переходя к пределу прив (1) – (3), получим точные равенства:

В (4) означает элемент длины дуги (дифференциал

(4) длины дуги) . Из (4) находим

. координаты центра масс кривой:

(5)

В частности, если масса распределена равномерно на , т.е., товыносится за интегралы и сокращается, и из (5) имеем:

, (6)

Если кривая задана явным уравнением, то формулы (5) и (6) остаются в

силе, только.

Пример. Найти координаты центра масс верхней части окружности:

, . C

Решение. . В силу симметрии кривой, сразу ясно, что .

Найдём: 0

. Итак, .

3) Вычисление давления жидкости на погруженную в неё пластину.

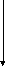
Пусть — удельный вес жидкости. Плоская пластинка, имеющая A

форму криволинейной трапеции , погружена вертикально в

жидкость. Верхняя часть её на глубине , нижняя – на . Нужно

найти давление жидкост и на эту пластину. Используем

известный факт: давление жидкости на горизонтальную площадку B

площади , погруженную на глубину , вычисляется по формуле:

.

Разобьём на элементарные части длины. Проведём ординаты точек деления, которые разобьют пластинку на элементарные полосы, которые приближённо можно считать прямоугольниками. Тогда площадь— ой полоски будет. Приближённо можно считать, что вся— я полоска расположена на одной глубине, и поэтому давление на неё (на заштрихованную часть) будет. Тогда давление на всю пластинку будет:. Равенство становится точным при. Но этот предел интегральной суммы для непрерывной функциина, поэтому он существует, и есть определённый интеграл. Таким образом:

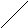
или

Если пластина ограничена слева кривой,

асправа -, то:

Пример. Найти давление воды на плотину, имеющую форму полукруга радиуса .

Решение. Найдём давление на половину плотины, тогда уравнение границы , и мы

имеем: 0

.

R

Тогда всё давление:

Применяются определённые интегралы и несобственные интегралы для вычисления и многих других величин (моментов инерции, центров масс плоской пластинки и т.п.).

14