4)По членное интегрирование и дифференцирование мажорируемых рядов.

Мы знаем, что производная (интеграл) от суммы нескольких функций равна сумме производных (интегралов) от отдельных слагаемых. Верны ли эти свойства для рядов? Т.е. справедливы ли равенства:

(1)

(2)

Если для сходящегося функционального ряда равенства (1) и (2) имеют место, то говорят, что функциональный ряд можно почленно интегрировать, дифференцировать. Существуют примеры, показывающие, что далеко не все функциональные ряды можно почленно дифференцировать, интегрировать. Но для мажорируемых они при наличие некоторых условий верны.

Теорема 1:

Если члены ряда есть непрерывные функции на [a;b] и ряд на [a;b] мажорируем, то его можно почленно интегрировать на [a;b].

Доказательство: Т.к. ряд мажорируем, то он сходится, его сумма S(x) есть функция непрерывная. Но тогда все интегралы в (2) существуют. Докажем само равенство (2). Ряд мажорируем, поэтому он сходится равномерно на [a;b]. Но тогда по " e>0 одновременно для "x принадлежит [a,b] существует N, что для "n³N выполняется неравенство (3) или короче . Возьмем произвольный номер n³N и зафиксируем его. Можно записать S_n(x)+r_n(x)=S(x). Т.к. S_n(x) и S(x) непрерывны, то и r_n(x) непрерывна на[a;b].Тогда (4). Т.к. S_n(x) состоит из конечного числа слагаемых, то

(5)

Оценим . Т.к.

b-a=const, это неравенство показывает, что для больших n: n³N, может быть сделана сколь угодно малой, т.е. , при n®¥.Из (4) имеем . Отсюда или по (5)

(6).

Т.к. есть n-ая частичная сумма числового ряда (2), то равенство(6) означает сходимость ряда (2) и равенство его суммы .

Замечание: Почленное интегрирование мажорируемого ряда совершенно так же можнопроизводить и по промежутку [a;x] : (При этомa£x£b).

Теорема 2:

Если ряд из непрерывных функций, имеющих непрерывные производные, сходится на [a;b] и его сумма есть S(x), а ряд, составленный из производных его членов (8) равномерно сходится на [a;b], то производная суммы ряда S'(x) равна сумме ряда из производных, т.е. справедливо (2). Короче говоря, в этом случае ряд можно почленно дифференцировать.

Доказательство: Ряд (8) по условию мажорируем. Тогда он сходится и пусть сумма u(x)= По теореме 1 ряд (8) можно почленно интегрировать на [a;b] и на "[a;x] (a£x£b).

Проинтегрируем: .

Продифференцируем (интеграл с переменным верхним пределом, u(x)-непрерывная).

5. Степенные ряды.

Определение:

Степенным рядом называется функциональный ряд вида:

(1),

где a_n и x₀ любые действительные числа.

В частности при x₀=0 ряд имеет вид

(2).

Степенной ряд (1)всегда можно привести к виду (2) заменой переменной x-x₀=y. Поэтому в дальнейшем для удобства будем говорить лишь о степенных рядах вида (2). Область сходимости степенного ряда всегда есть интервал, который может вырождаться и в точку. Установить это поможет теорема.

Теорема 1(Абеля):

1)Если степенной ряд (2) сходится при некотором значении , то он абсолютно сходится при любых значениях х, удовлетворяющих неравенству .

2)Если степенной ряд (2) расходится при некотором значении , то он расходится и при любых значениях x, удовлетворяющих неравенству .

Доказательство:

1. По условию числовой ряд сходится. Но тогда предел его общего члена равен 0: 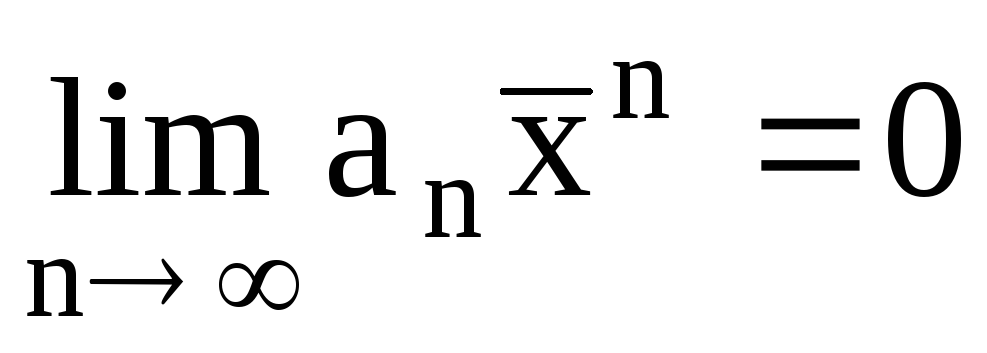. Это означает, что найдется такое число M>0, что для всех n(n=1,2,3,...) будет справедливо неравенство . Возьмем произвольное x удовлетворяющее неравенству . Рассмотрим ряд

(3).

Оценим: . Но справа - общий член сходящийся геометрической прогрессии со знаменателем . Тогда по теореме сравнения для ряда с положительными членами ряд (3) сходится. Но сходимость ряда (3) означает абсолютную сходимость ряда (2) в точке x. Т.к. x любое число то, теорема доказана.

2) Пусть в ряд (2) расходится. Пусть x' любая точка, такая, что .Допустим, что ряд в ней сходится. Но тогда попервой части он должен сходитсяво всех точках x таких, что . Но . Значит, ряд должен сходится в точке , чего нет. Противоречие доказывает теорему.

Теорема Абеля имеет простой геометрический смысл: если степенной ряд сходитсяв одной точке , то он сходится и в целом интервале , с центром вточке О.Если он расходится в некоторой точке , то он расходится в двух бесконечных интервалах.

Но т.к. степенной ряд определен на всей прямой, то в каждой точке он сходится или расходится. Отсюда немедленно вытекает существование пограничных точек между сходимостью и расходимость, т.е. существует такое число R>0, что для ряд абсолютно сходится, для расходится.

Определение 1:

Число R>0 такое, что степенной ряд для всех абсолютно сходится, а для всех расходится и называется радиусом сходимости степенного ряда.

Определение 2:

Интервал (-R;R) называется интервалом сходимости.

Ясно, что внутри интервала сходимости степенной ряд сходится абсолютно, вне его расходится. На концах интервала, т.е. в точках x=-R и x=R степенные ряды могутсходиться и расходиться, сходиться на одном, расходиться на другом. Из сказанного следует:

Теорема 2:Областью сходимости степенного ряда может быть один из промежутков [-R;R], (-R;R], [-R;R), (-R;R).

Вывод: Для нахождения области сходимости степенного ряда нужно найти его радиуссходимости R и исследовать его сходимость на концах, т.е.приx=-R и x=R. Следуетзаметить, что степенной ряд может сходиться во всех точках прямой, тогда полагают R=¥ и интервал сходимости (-¥,+¥), может сходится и тольков одной точке x=0, тогда и R=0.

Например:

1. Ряд . Возьмем "x₀Î(-¥,+¥). Всегда можно подобрать номер n, чтобы выполнялось неравенство - общий член сходящийся геометрической прогрессии с . Тогда сходится и ряд , а, значит, и данный. Но x₀-любая точка (-¥.+¥)ÞR=¥.J=(-¥.+¥).

2. Ряд . В точке x₀=0S(0)=0 - ряд сходится. Пусть x₀¹0. Можно взять n столь большим, что . Но тогда и потому . Не выполнен необходимый признак, ряд расходится. Итак J={0},R=0.

Находить концы сходимости степенного ряда по его коэффициентам позволяют следующие две теоремы, основанные на признаках абсолютной сходимости Даламбера иКоши.

Теорема 3:

Если коэффициенты степенного ряда таковы, что выполняется условие , то радиус сходимости степенного ряда

Доказательство: Т.к. в (-R;R) степенной ряд должен сходится абсолютно, то R можем найти исследуя его на абсолютную сходимость. Применим признак Даламбера.

Отсюда следует, что степенной ряд сходится абсолютно для тех x, для которых <1 и расходится для тех x, для которых >1.

Если 0<D<¥, то и потому .

Если D=¥, то неравенство для "x¹0. Потому во всех точках x¹0 ряд расходится ÞR=0.

Если D=0, то для любых x и потому R=¥.

Теорема 4:

Если коэффициенты ряда таковы, что выполняется условие: , то радиуссходимости степенного ряда

Доказательство аналогичное (самостоятельно).

Замечание: Чаще на практике находят R по формулам:

(a_n -коэффициенты общего члена).

Пример: Найти область сходимости степенного ряда

Применим теорему 3: ,R=1,J=(-1;1). Исследуем сходимость на концах интервала сходимости.

x=1. Подставим в ряд: Он сходится по теореме Лейбница (более того - он сходится абсолютно).

x=-1. Подставим в ряд: . Ряд сходится абсолютно (как обобщенный гармонический ,s=2>1).

Итак, область сходимости данного степенного ряда есть [-1;1], ряд в точках отрезка сходится абсолютно, вне - ряд расходится.