РЯДЫ

1.Числовые ряды.

1) Основные понятия и определения

Пусть имеется некоторая бесконечная последовательность чисел:

, , ... , , ..., (1)

Составляемый из этих чисел символ

+ + ... + + ...(2)

называется бесконечнымчисловым рядом или просто числовым рядом. Сами числа ,,...,,... называютсячленами ряда, n-ый член называются общим членом ряда (2). Часто для сокращения вместо (2) пишут - , т.е.

+ + ... + + ... = (3)

Будем последовательно складывать члены ряда и полученные суммы называть частичными суммами ряда: =, = + , =++, ..., =+++...++... Получаем бесконечную последовательность {}.

Определение: Если существует предел S последовательности частных сумм S =, то его называют суммой ряда (2) и говорят, что ряд (2) сходится.

Символически это записывают S=.

Если же предел не существует, ряд называют расходящимся. Если =, то, все равно, ряд считают расходящимся, не имеющим конечной суммы.

Пример: Рассмотрим ряд,

(4),

который обычно называют бесконечной геометрической прогрессией, q-знаменатель, а¹0. Исследуем сходимость этого ряда (4). Найдем его n-ую частичную сумму {}. Очевидно или

= (5).

Рассмотрим все возможные варианты:

а)<1. Тогда и =существует и конечен. Ряд сходится.

б) >1. Тогда при , не может быть конечным. Ряд расходится.

в)q=-1.Тогда ряд (4) имеет вид a - a + a - a + a - a +..., т.е. =0 при nчетном и =a при nнечетном, но поэтому не существует. Ряд расходится.

г) q=1. Тогда ряд (4) имеет вид a+a+a+..., = , = в зависимости от знака а.Ряд расходится.

Вывод: Бесконечная геометрическая прогрессия - сходится при <1 и сумма ее в этом случае S=.Во всех остальных случаях она является расходящимся рядом.

2. Основные свойства сходящихся рядов.

Будем говорить о свойствах присущих всем сходящимся рядам. Условимся об одномпонятии. Если в ряде (1) отбросить первые m членов, то получится рядa_m+1 +a_m+2 + ... = (2), называемый остатком ряда (1) после m-ого члена.Еслиряд (2)сходится,то его сумма обычно обозначаетсяR_m.

Теорема 1:

Если сходится ряд (1), то сходится и любой из его остатков.Наоборот: из сходимости некоторого остатка следует сходимость самого ряда.

Доказательство:

1)Пусть ряд - сходится и его сумма S.Рассмотрим остаток после m-ого члена- . Он ряд, его k-аячастичная сумма имеет вид

=a_m+1+ a_m+2 +...+=a₁+a₂+...+a_m+a_m+1+...+-(a₁+a₂+...+a_m)=

=-S_m.

Итак: =

Перейдем к пределу при :

- конечное число. Значит, последовательность{}частичных сумм остатка сходятся, т.е. сходится остаток.

2. Наоборот: пусть сходится некоторый остаток после m-го члена - и его суммаR_m . Рассмотрим частичные суммы ряда (1) с номерамиp>m, т.е.p=m+k.Тогдаочевидно S_p = S_m+k= S_m+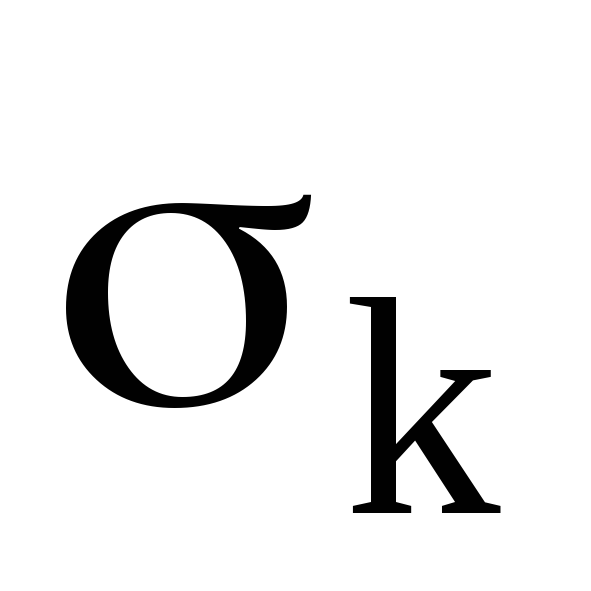. Если , то и , т.к.m-фиксировано. Перейдем к пределу при .

- конечное число. Отсюда и следует сходимость ряда (1).

Следствие: Добавление или отбрасывание в начале ряда конечного числа новых членов не нарушает его сходимость (может изменится только сумма, если ряд сходящийся)

Теорема 2:

Если ряд (1) сходится, то сумма R_m его остатка после m-огочлена стремится к 0при .

Доказательство:

Ряд - сходится и S-его сумма.Тогда S=S_m + R_m. Откуда R_m=S - S_m.

=S - S=0

Замечание: Теорема 2 показывает, что сумму сходящегося ряда (1) можно приближенно найти, взяв сумму первыхmчленов. Чем большеmтем меньше сумма всех отброшеных и точность выше.

Теорема 3:

Пусть ряд - сходится и сумма его есть S. Если все членыряда умножить на одно и тоже число c0, то новый ряд - будет тожесходиться и сумма его равна .

Доказательство:

Возьмем частичную сумму ряда;

=ca₁+ca₂+...+ca_n =c(a₁+...+a_n) =. Перейдем к пределу

.

Теорема 4:

Пусть даны два сходящихся ряда - =A(3)и =B(4).Еслисоставить новый ряд путем почленного сложения (или вычитания) соответствующихчленов этих рядов - (5), то этот новый ряд также будет сходиться иего сумма S' равна сумме (разности) сумм исходных рядов S'=

Доказательство:

Рассмотрим частичные суммы ряда (5).

=. Перейдем к пределу: S'=.

Вывод:Сходящиеся ряды можно умножить на число, почленно складывать и вычитать как конечные суммы.

3)Необходимый признак сходимости ряда.

Мы видим, что сходящиеся ряды обладают радом особых свойств. Поэтому важно знать- сходится данный ряд или нет.Нахождение суммы Sряда часто бывает трудным.Поэтомуустановлены различные признаки сходимости рядов, позволяющие судить о сходимостиили расходимости ряда не находя его суммы. Сейчас рассмотрим необходимый признак сходимости ряда,т.е. такое условие,при невыполнении которого ряд обязательно расходится.

Теорема:

Если ряд - сходится, то предел его общего членапри равен0: .

Доказательство:

Т.к. ряд сходится, то , но . Перейдемк пределу в последнем равенстве

Следствие: Если , то ряд обязательно расходится.Если бы он сходился, то по теореме бы, чего нет.

Пример:

,

- ряд расходится.

Покажем, что это условие не является достаточным, т.е. что при наличии условия , ряд может все таки расходится.

Покажем это на примере, так называемого, гармонического ряда.

(1)

Сгруппируем члены ряда следующим образом:

Каждая из групп в сумме >.Возьмем произвольную:

Рассмотри теперь подпоследовательность частичных сумм гармонического ряда (1) сномерами (к=1,2,3...).

Получим:к=1, S₁ = 1 >

к=2, S₃ =

к=3, S₇= и т.д.

.

Но при и поэтому подпоследовательность{}возрастает и неограничен сверху. Поэтому эта подпоследовательность расходится,а, значит, и вся последовательность частичных сумм {S_n} гармонического ряда тем болеерасходятся. Значит, расходится сам ряд.

Необходимый признак сходимости справедлив для любых числовых рядов. Достаточные признаки сходимости установим дляотдельных видоврядов.

4)Ряды с положительными членами. Достаточные

признаки их сходимости.

Это ряды , члены которых положительны a_n>0 (n=1,2,...).Иногда допускают, что некоторые члены равны 0, т.е. , чтобы не менятьнумерации.

Лемма: Если частичные суммы ряда с положительными членами ограничены сверху: < M,то ряд сходится.

Доказательство:

Частичные суммы , т.к. и , т.е. последовательность {}сумм является монотонно неубывающей. Но по условию она ограниченасверху, а потому имеет конечный предел , рядсходится.Ясно также, что .

Замечание: Если {} не ограничена сверху, то ряд расходится, т.к. .

Спомощью леммы установим удобные напрактике достаточные признаки сходимости, которые называются признаками сравнения.

Теорема 1:

Пусть даны два ряда с положительными членами

(1) и

(2)

и пусть каждый член ряда (1) не больше соответствующего по номеру члена ряда (2): (n=1,2,3,...). Тогда :

1) если сходится ряд (2), то сходится и ряд (1);

2) если расходится ряд (1), то расходится и ряд (2)

Доказательство:

Докажем 1)

Пусть ряд (2) сходится и S¢ его сумма: . Для nимеем . Частичная сумма ряда (1)

, т.е. для n , значит последовательность частных сумм ряда (1) ограничена сверху и потому по лемме ряд (1) сходится.

Докажем 2)

Пусть ряд (1) расходится. Тогда и стремится монотонно. Но , а потому тем более.

Поэтому , ряд (2) расходится.

Если сходится ряд с большими членами, то сходится и с меньшими, если расходится с меньшими, то расходится и с большими.

Пример: Ряд сравним с рядом гармоническим ,т.к. гармонический ряд расходится, то расходится и данный ряд.

Замечание: Теорема 1 верна и тогда, когда неравенство начинается не сразу с первого номера n=1, а хотя бы с n=N (n=N+1, n=N+2...).

Доказательство:

Первые N членов можно отбросить, на сходимость ряда это не влияет. Дальше рассуждаем аналогично.

Из теоремы 1 вытекает удобное на практике следствие.

Следствие:Если существует конечный предел (), то из сходимостиили расходимости одного ряда следует сходимость или расходимость другого.Заметим сразу, что следствие верно для строго.

Доказательство:

Пусть конечный существует. Тогда поопределению предела для для n>N или или (3). Допустим ряд - расходится. Тогда по теореме 1 в силу (3) расходится иряд ,а, значит, и ряд. (Если бы - сходился, то сходился бы и - ). Т.к. то . Аналогично рассуждая, получим: из расходимости следует, что расходится . Пусть ряд - сходится, тогда и ряд - тоже сходится. Но по теореме 1 из (3) следует тогда сходимость ряда . Исходя из аналогично получим из сходимости сходимость ряда (из расходимости - расходимость).

Пример: (1)Сравним с гармоническим рядом (2).

(первый замечательный предел). Ряд (2) расходится, (1) тоже.

Довольно часто в качестве ряда для сравнения берут сходящуюся геометрическую прогрессию . Сравнивая ряд (1) с этим рядом, получаем еще два удобных признака Даламбера и Коши (достаточные).

Теорема 2 (признак Даламбера):

Если в ряде с положительными членами существует конечный предел при отношения последующего члена к предыдущему равный , (4),то при <1 ряд сходится, при >1 ряд расходится. При =1ничего определенного сказать нельзя: ряд может сходиться или расходиться.

Доказательство:

Пусть существует .

1)<1. По определению предела для с некоторого номера N, т.е. для всех выполняется неравенство

, (5)

Т.к. выполняется(5) для , то можем считать столь малым, что . Обозначим . Тогда или

и т.д.

Рассмотрим теперь два ряда

(6)

(7)

Ряд (7) есть геометрическая прогрессия со знаменателем , а потому сходится. Но тогда по теореме 1(сравнения) сходится и ряд (6). Но ряд (6) является остатком ряда (1) после N-ого члена. А потому сам ряд (1) тоже сходится.

2) . Тогда для достаточно малых можем считать , и, начиная с номера N выполняется в силу (5) неравенство (n=N,N+1, N+2, ...). Отсюдаследует , что . Но тогда члены ряда монотонно возрастают, а потому , т.е. не выполняется необходимый признак сходимости. Ряд расходится.

3) . Здесь подобные рассуждения не проходят. Примеры же показывают, что в этом случае ряд может сходится и расходится. Нужно применять другие признаки. (Примеры таких рядов будут приведены позже).

Пример: ,

, (второй замечательный предел), значит, ряд расходится.

Замечание: Если , то теорема не дает ответа о сходимости ряда. Но если отношение остается >1 все время, то ряд расходится. В этом случае и потому не выполняется необходимый признак сходимости.

Пример: ,

Признак Даламбера не даёт ответа , но видно , что и по замечанию ряд расходится .

Теорема 3 (признак Коши):

Если в ряде с положительными членами величина имеет конечный предел , при ,т.е. (8), то при <1 ряд сходится, при >1 ряд расходится. При =1 ничего определенного сказать нельзя, ряд может сходиться и расходиться.

Доказательство:

Пусть существует .

1)Пусть <1. По определению предела для >0 начиная с некоторого номера N, т.е. для n³N выполняется неравенство или (9). Т.к. сколь угодно мало, то число . Обозначим . Тогда для всех . Или для всех , т.е. ,. Рассмотрим теперь два ряда

(10)

(11)

Ряд (11) является геометрической прогрессией, которая сходится, т.к. . Тогда сходится и ряд (10) по теореме сравнения. Но (10) есть остаток ряда (1), а потому и ряд (1) сходится.

2) Пусть . Тогда для достаточно малых можем считать . Обозначим . Тогда из (3) следует для , т.е. , т.е. , а это значит, что не может быть меньше 1, т.е. не равен 0. Необходимый признак не выполняется, ряд (1) расходится.

3)Если , то рассуждения не проходят. Примеры показывают что, ряд может как сходиться, так и расходится. Нужны другие признаки для исследования.

Пример 1: Исследовать на сходимость ряд . Применим признак Коши.

. Ряд сходится.

Пример 2: Исследовать на сходимость обобщенный гармонический ряд ,s - любое положительное число. Применим признак Коши: . Он ответа не дает. Применим признак Даламбера:

. Нет ответа.

Этот пример показывает, что признаки Даламбера и Коши удобны, но применимы не всегда. Существует много других признаков сходимости более сильных, но и более сложных (Куммера, Гаусса, Раабе и др.).

Мы разберем еще один признак сходимости рядов с положительными членами, основанный на использовании несобственного интеграла и применимый во многих случаях.

Теорема 4 (интегральный признак Коши):

Пусть члены ряда

(1)

положительные и не возрастают, т.е.

, (2),

и существует положительная непрерывная невозрастающая функция f(x) на [1,+¥] такая, что f(1)=a₁,f(2)=a₂,...,f(n)=a_n,...Тогда ряд (1) сходится, если сходится несобственный интеграл и расходится, если расходится этот интеграл.

Доказательство: Проведем его геометрически. Построим график функции y=f(x). Отметим на графике точки с абсциссами 1,2,3, ... ,n-1, n,... Построим систему выходящих и систему входящих прямоугольников. Рассмотрим криволинейною трапецию, ограниченную линией y=f(x) с основанием от x=1 до х=n , где n- произвольное натуральное число.

Площадь этой трапеции численно равна определенному интегралу . Рассмотрим фигуру составленную из выходящих прямоугольников с основанияви от 1 до n. Площадь 1 прямоугольника равна 1×f(1)=f(1)=a₁, площадь 2 прямоугольника равна 1×f(2)=f(2)=a₂,..., площадь n-1 прямоугольника равна 1×f(n-1)=f(n-1)=a_n-1..Тогда площадь всей фигуры (выходящей) равна a₁+a₂+...+a_n-1=S_n-a_n(S_n-n-ая частичная сумма ряда (1)). Аналогично площадь входящей фигуры равна 1×f(2)+1×f(3)+...+1×f(n)=a₂+a₃+...+a_n=S_n-a₁. Из чертежа ясно, что площадь трапеции J_n заключена между площадями входящей и выходящей фигур S_n-a₁<J_n<S_n-a_n или S_n-a₁<<S_n-a_n (*). Заметим, что т.к. функция f(x) положительная, то интеграл J_n возрастает с возрастанием n. Рассмотрим два возможных случая.

1)Несобственный интеграл сходится, т.е. имеет конечное значение J. Т.к. , то в силу (*) имеем . Т.е. последовательностьчастичных сумм S_n ограничена сверху. Тогда по лемме ряд (1) сходится.

2)Несобственный интеграл расходится, т.е. . Это значит, что интеграл неограниченновозрастает при возрастании n.В силу неравенства(*) и потому S_n тем более неограниченно возрастает при , т.е. ряд расходится. Теорема доказана.

Пример: Исследуем обобщенный гармонический ряд ,s - любое положительное число. Применим интегральный признак Каши: функция на [1,+¥] удовлетворяет всем требованиям теоремы 4, ряд тоже.Рассмотрим интеграл:

.

Пусть s>1. Тогда , т.е. интеграл конечен, ряд сходится.

Пусть s<1. Тогда , интеграл расходится, значит, и ряд расходится.

Пусть s=1. Тогда , ряд расходится (это еще раз подтверждает расходимость гармонического ряда ).

Вывод: Обобщенный гармонический ряд сходится при S>1 и расходится при S£1(S>0).

Пример: , ряд расходится. , ряд сходится.

Замечание: Мы доказали, что признак Коши и Даламбера дают 1 в пределе при исследовании обобщенного гармонического ряда на сходимость независимо от (S). Но при S>1 ряд оказывается сходящимся, при S<1 расходящимся, т.е., действительно, в этом случае признаки Коши и Даламбера не дают ответа.

5) Знакочередующиеся ряды. Их сходимость.

Определение: Знакочередующимся рядом называется такой ряд, у которого поочередно члены имеют положительное и отрицательное значение.

Принято записывать знакочередующиеся ряды в таком виде, чтобы знаки членов были сразу видны. При этом можно считать, что первый член положителен, в противном случае можно умножить ряд на

(-1), что на сходимости не отразится.

(1)

При этом все a_n>0. Сходимость знакочередующегося ряда (1) удобно исследовать с помощью следующего достаточного признака.

Теорема (Лейбница) :

Если в знакочередующемся ряде (1) члены монотонно убывают по абсолютной величине: a₁>a₂>a₃>...>a_n>... , и стремятся к0при , то этот ряд сходится, егосумма положительна и не превосходит первого члена.

Доказательство: Рассмотрим частичные суммы ряда (1), содержащие четное число членов S_n=S_2m изапишем S_2m=(a₁-a₂)+(a₃-a₄)+...+(a_2(m+1)-a_2m). В круглых скобках стоят положительные числа т.к. a₁>a₂,a₃>a₄,... Но тогда S_2m>0 и с возрастанием m возрастает. С другой стороны S_2m=a₁-(a₂-a₃)-(a₄-a₅)-...-(a_2(m-2)-a_2(m-1))-a_2m<a₁т.к. из a₁ вычитаются все время положительные числа. Т.к. {S_2m} возрастает и ограничена сверху, то она имеет предел. Причем, очевидно, 0<S<a₁ Но сходимость ряда (1) еще неустановлена. Нужно показать, что и последовательность {S_2(m+1)} частичных сумм,содержащих нечетное число членов сходится и к тому же числу S. S_2m+1=a₁-a₂+a₃-...+a_2m.Очевидно S_2m+1=S_2m+a_2m+1. Перейдем к пределу при m®¥:

.

Итак, и четные и нечетные суммы S_n стремятся к одному и тому же пределу S. Т.е. ряд (1) сходится, его сумма 0<S<a₁.

Теорему Лейбница можно проиллюстрировать геометрически. Предварительно заметим, что последовательность {S_2m+1} монотонно убывает при стремлении к S т.к. S_2m+1=a₁+(a₂-a₃)-... то с возрастанием номера отa₁ вычитаются все новые положительные слагаемые. Это и показывает, что S_2m+1 монотонно убываетпри . Отсюда ясно, что числа S_m располагаются поочередно слеваи справа от S, постепенно приближаясь к нему

0 S₂ S₄ S₆ S S₅ S₃ S₁=a₁

Замечание 1:Если бы знакочередующийся ряд начинался с отрицательного члена -a₁+a₂-a₃+...,то геометрическая иллюстрация должна бы симметрично отобразится относительноточки О, сумма S была бы отрицательна и было бы верно неравенство

S₁=a₁ S₃ S S₄ S₂ 0

Это неравенство справедливо и в первом случае.

Замечание 2:Остаток ряда типа Лейбница тоже является знакочередующимся и удовлетворяет теореме Лейбница. Поэтому , т.е. остаток ряда по абсолютной величине не превосходит первого своего члена. Это используется в приближенных вычислениях. Можно приближенно находить величину суммы знакочередующегося ряда и при этом оценить величину возможной погрешности. Взяв n первых членов ряда (1) S_n, мы можем считать , при этом S_n отличается от точной величины суммы на сумму остатка r_n, а т.к. ,то ошибка вычисления меньше абсолютной величины первого отброшенного члена.

Пример: Ряд удовлетворяет всем условиям теоремы Лейбница, т.к. и убывает монотонно.

Найдем сумму 4 членов. . Погрешность вычисления на величину . Значит, с возможной погрешностью не более . Если взять большее число членов, то погрешность будет еще меньше, а, значит, точность выше.

6. Знакопеременные ряды. Абсолютная и условная

сходимость.

Пусть числовой ряд (1) состоит как из положительных, так и отрицательныхчленов, которые встречаются в любом порядке (не обязательно чередуются). К такому ряду можно применить только необходимый признак сходимости, но он дает ответ лишь о расходимости ряда. Признаки же остальные для этих рядов не годятся.Но часто о сходимости знакопеременного ряда (1) можно судить по ряду, составленному из абсолютных величин членов ряда (1) -(2),который является уже рядом с положительными членами.

Теорема:

Если знакопеременный ряд (1) таков, что ряд, составленный из абсолютныхвеличин его членов (2) сходится, то сходится и сам ряд (1).

Доказательство: Обозначим через S_n сумму n первых членов ряда (1) ,через сумму всех положительных, а через сумму абсолютных величинвсех отрицательных членов среди этих n первых членов ряда.Обозначим через G_n сумму n первых членов ряда (2). , тогда S_n=-, G_n=+. По условию ряд (2) сходится, потому существует его сумма . Но тогда возрастающие и ограниченные сверху числом G величины и тем более имеют предел и , но тогда -конечное число. Значит, ряд (1) действительно сходится.

Пример: Исследовать на сходимость ряд

(3)

Составим ряд из абсолютных величин

,

он сходится, т.к. это обобщенный гармонический ряд: . Тогда сходится и ряд (3). Теорема дает только достаточный признак сходимости, поэтому в случае расходимости ряда (2) из абсолютных величин ничего определенного о сходимости ряда (1) еще сказать нельзя.

Определение1:

Знакопеременные ряд называется абсолютносходящимся, если сходится ряд из абсолютных величин его членов.

Определение 2:

Если знакопеременный ряд (1) сходится, а ряд из абсолютных величин его членов (2) расходится, то ряд (1) называют не абсолютно или условно сходящимся.

Различия у абсолютно и условно сходящихся рядов довольно важные. Например, члены абсолютно сходящегося ряда можно как угодно переставлять, он по прежнему будет сходится и его сумма останется прежней. Перестановка же членов условно сходящегося ряда может изменить его сумму и даже сделать ряд расходящимся. Покажем это на примере. Возьмем условно сходящийся ряд Переставим его члены так, чтобы после каждого положительного стояло два отрицательных: , сложим положительный с последующим отрицательным, получим:

Если сумма первого ряда S, то сумма второго ряда .

Абсолютно сходящиеся ряды можно перемножать. При этом произведением двух таких рядов

(4)

(5)

называется ряд образованный из всевозможных парных произведений, записанных в таком порядке.

В каждой скобке члены имеют одинаковую сумму индексов.

Теорема:

Если ряды (4) и (5) абсолютно сходятся и их суммы S₁ и S₂, то их произведение тоже есть абсолютно сходящийся ряд, сумма S которого равна произведению сумм этих рядов S=S₁×S₂.