3 Метод Остроградского.

Пусть нужно вычислить где знаменатель Q(x) имеет

кратные комплексные корни, т. е. разложение Q(x) имеет квадратичные множители в степени  2 /2, 3, 4,…/. Тогда разложение (3) дроби ^P(x)_/Q(x) в сумму простейших содержит дроби IV типа. Именно в этом случае более выгодным является метод

Остроградского, который позволяет заменить вычисление интеграла

вычислением интеграла , где разложение Q₁(x) содержит квадратичные

множители (и линейные тоже!) только в первых степенях. Поступают так:

Пусть имеем где Q(x) = (x – a)^ … (x – b)^β(x² + px + q)^μ … (x² + lx + s)^ν.

Представим Q(x) в виде произведения двух множителей

Q(x) = Q₁(x) ∙ Q₂(x),

причём Q₁(x) есть произведение всех разных множителей из Q(x) взятых по одному разу

Q₁(x) = (x – a) … (x – b)(x² + px + q) … (x² + lx + s),

а Q₂(x) есть произведение оставшихся неиспользованными сомножителей из Q(x)

Q₂(x) = (x – a)^{ – 1} … (x – b)^{β – 1}(x² + px + q)^{μ – 1} … (x² + lx + s)^{ν – 1}.

Остроградский (известный русский учёный) доказал следующую формулу:

(6)

Здесь Q(x), Q₁(x), Q₂(x), известные многочлены, степени которых есть соответственно m, m₁, m₂. P(x) тоже известный многочлен степени ≤ m – 1. P₁(x) и P₂(x) есть пока ещё неизвестные многочлены степеней соответственно не выше m₁ – 1 и m₂ – 1 /все дроби правильные/:

/a₁, a₂, … b₁, b₂, … – неизвестные пока (буквенные) коэффициенты /.

Для нахождения этих коэффициентов продифференцируем равенство (6):

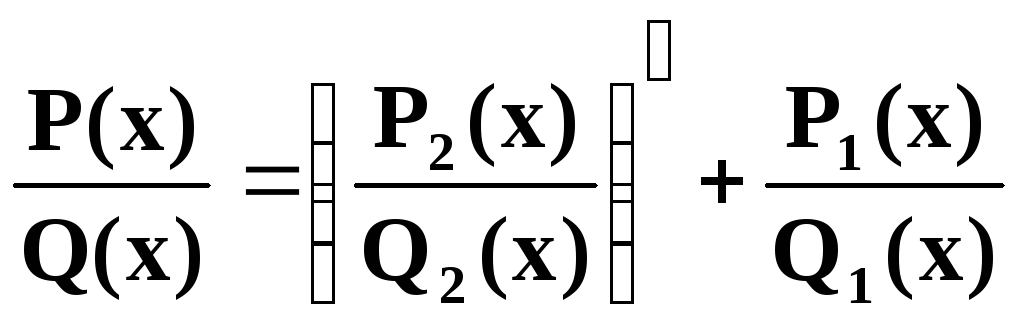
(7)

По методу неопределённых коэффициентов мы найдём из (7) коэффициенты, а, значит, и многочлены P₁(x) и P₂(x). Подставим их в (6) и останется только вычислить

,

где Q₁(x) в своём разложении содержит разные множители только в первых степенях.

Примеры. 1)

Применим метод Острограденного, т. к. Q(x) содержит множитель (x² + 1)².

Q(x) = (x + 1)(x² + 1)² /m = 5/

Q₁(x) = (x + 1)(x² + 1) /m₁ = 3/ тогда P₁(x) = cx² + dx + k

Q₂(x) = x² + 1 /m₂ = 2/ P₂(x) = ax + b

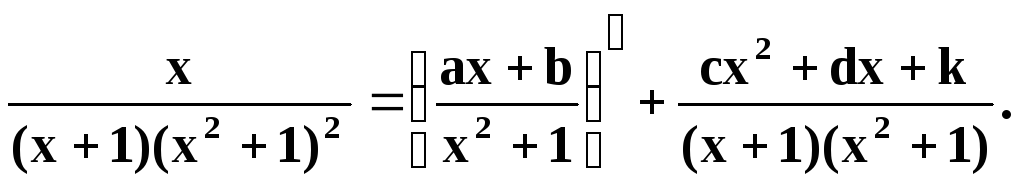
Запишем (7):

или

Данная и полученная дроби тождественно равны и имеют одинаковые знаменатели, поэтому их числители должны быть тоже тождественно равны. Но тогда коэффициенты при соответствующих степенях тоже равны:

получаем: a = ¼, b = – ¼, c = 0, d = ¼, k = – ¼.

Тогда по (6) имеем

I₁ вычисляем как раньше:

отсюда Ax² + A + Mx² + Nx + Mx + N ≡ x – 1 и

A = – 1, M = 1, N = 0

2) Вычислить

Ответ:

§6 Интегрирование некоторых иррациональных функций.

Функция f(x) называется иррациональной, если она получена с помощью четырёх рациональных операций (сложения, вычитания, умножения, деления) и возведения в рациональную степень (не целую) переменной интегрирования или некоторого рационального выражения от этой переменной.

Далеко не всегда можно выразить интеграл от иррациональной функции с помощью элементарных функций (интеграл “не берётся” в конечном виде).

Мы рассмотрим некоторые наиболее употребительные иррациональные выражения, неопределённые интегралы от которых могут быть выражены через элементарные функции.

1) Интегрирование выражений R (x,x^m/n,…,x^r/s), где m/n,...,r/s рациональные дроби. Здесь символ R (x,x^m/n,…,x^r/s) означает, что над x,x^m/n,…,x^r/s производятся только рациональные действия (четыре перечисленных выше и возведение в натуральную степень). /“R”=”рациональное выражение от...”/. Пусть k – наименьший общий знаменатель дробей m/n,...,r/s. Осуществим замену X = t^k , тогда dx = kt^k-1dt.

Каждая дробная степень X тогда выразится через натуральную степень t и потому

подинтегральное выражение станет рациональной функцией от t. В этой связи замену X = t^k называют рационализирующей подстановкой.

Пример. Вычислить неопределённый интеграл

Решение. Т. к. то наименьший общий знаменатель дробей 1/3 и 1/6

будет6. Потому берём x = t⁶ , откуда dx = 6t⁵dt и . Тогда

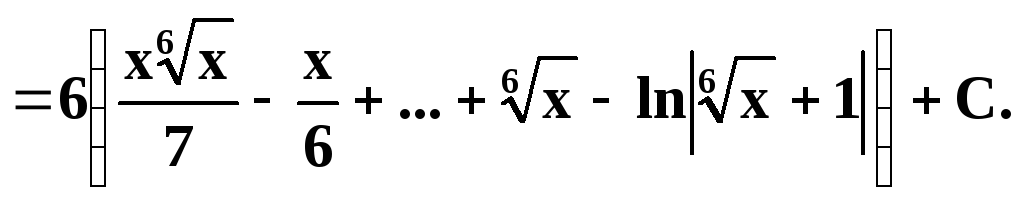
2. Интегрирование выражений

Пустьk – наименьший общий знаменатель дробей m/n, … ,r/s. Осуществляя замену

мы сведём интеграл от этого иррационального выражения к интегралу от

рационального выражения по t.

Пример. Вычислить интеграл

Положим

• интеграл от

• рациональной. функции.

Разлагаем подинтегральную функцию на простейшие рациональные дроби по методу неопределённых коэффициентов:

Затем проинтегрируем их и перейдём в результате к первоначальному аргументуx.