§11. Векторное произведение двух векторов.

Рассмотрим снова обычное векторное пространство геометрических векторов R (его размерность равна 3). В нем рассмотрим некоторую декартову систему координат O, e₁, e₂, e₃, причем для определенности считаем ее правой, т.е. такой в которой кратчайший поворот первого вектора ко второму, если смотреть с конца третьего, осуществляется против хода часовой стрелки (если по часовой, то тройка будет левая). Заметим, что так определяется правая и левая тройки для любых трех некомпланарных векторов.

1. Определение векторного произведения и его основные свойства.

Определение: Векторным произведением двух векторов a и b называется такой третий вектор c, которой строится по следующим правилам:

1. Векторы a и b приводятся к общему началу О и вектор c откладывается от точки О перпендикулярно плоскости векторов a и b.

2. Векторы a, b, c должны составлять правую тройку.

3. Модуль вектора c равен площади параллелограмма, построенного на векторах a и b.

Обозначается векторное произведение ab=c или [a,b]=c.

Например: если e₁, e₂, e₃ – правый ортонормированный базис, то

e₁e₂=e₃, e₂e₃=e₁, e₃e₁=e₂

Понятие векторного произведения исходит из механики. Если вектор Fизображает силу, действующую на точку М – конец вектораa=ОМ, тоaFпредставляет момент силыFотносительно точки О (здесь векторa- плечо)

Отметим основные свойства векторного произведения:

1. Модуль векторного произведения равен произведению модулей перемножаемых векторов на синус угла между ними. |ab| = |a| |b| sin (следует из определения п. 3)

2. Векторное произведение обращается в нуль тогда и только тогда, когда эти векторы коллинеарны.

Доказательство:1) Пустьab=0 => |ab| = |a| |b| sin = 0. Это возможно если |a| = 0 или |b| = 0 или sin  = 0. В первых двух случаях один (или два) вектора нулевые, то есть они не имеют определенного направления и их можно считать коллинеарными.

Если sin  = 0, то= 0 или 180⁰=>a||b.

2. Пусть a || b =>  = 0 или 180⁰ => sin  = 0 => |ab| = 0 => ab = 0

Что и требовалось доказать.

3. Свойство антиперестановочности [a, b] = - ab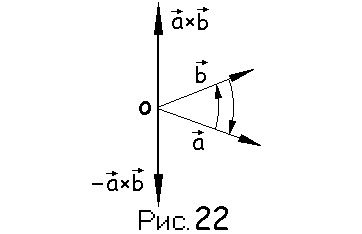

На самом деле, из определения следует, что модуль векторного произведения не зависит от порядка сомножителей, векторы ab || ba, но переставляя сомножители мы обязаны изменить направление произведения, чтобы тройка векторов осталась правой. Действительно, еслиa,b,ab– правая, тоb,a,ba – левая,b,a,-ab– опять правая. (см. рис 22)

4. Для любых векторов a,bиcи любых чиселиимеет место равенство:

(a+b)c = (ac)+(bc)    и    [a, bc] = [a, b]+[a, c]

• распределительное свойство (без доказательства).

5. Для любых векторов a,bи любых чиселиимеет место равенство:

a(b) = (ab)    и    (a)(b) = ()(ab)

• сочетательность относительно умножения на число (без доказательства).

2) Выражение векторного произведения через координаты перемножаемых векторов.

Пусть векторы a= {₁,₂,₃} иb = {₁,₂,₃} заданы своими координатами в базисеe₁,e₂,e₃. Тогда, применяя свойства 4 и 5 получим:

Учитывая, что в случае ортонормированного базиса i,j,k:

Мы получим теорему:

Теорема:В ортонормированном базисе векторное произведение выражается через координаты сомножителей в виде:

Используя определитель третьего порядка предыдущую формулу легко переписать в виде:

(легко видеть, раскрыв определитель по элементам первой строки)

Следствие: Если векторы aиbколлинеарны:a||b, то согласно свойству 2ab=0. Но это значит, что все три координаты вектораabобращаются в нуль:

₁₂ – ₂₁=0

₂₃ – ₃₂=0  или  =>

₃₁ – ₁₃=0

Итак:Условием коллинеарности двух векторов является пропорциональность их координат.

3. Вычисление площади треугольника.

Из определения векторного произведения векторов aиbследует, что площадь параллелограмма, построенного на них:S= |ab|.

Тогда площадь треугольника, стороны которого есть вектора aиb:

S _треуг =|ab| / 2.