§9. Скалярное произведение векторов.

Вернемся в обычное векторное пространство геометрических векторов.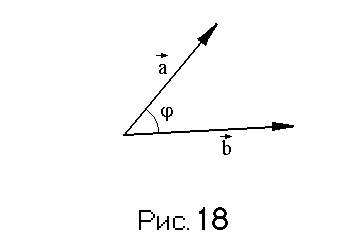

Имеются два вектора a и b. Угол между ними – это наименьший из двух углов (для векторов, приведённых в одно начало) обозначают  = (a ^ b) 0 (см. рис 18)

Если =/2, то такие вектора называются ортогональными.

Определение: Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначается скалярное произведение (a , b)

Итак (a , b) = | a || b |cos , где  = (a ^ b)

Очевидны свойства скалярного произведения:

1. (a,b) = (b,a) (коммутативность)

2. (a , a) = |a|² для любого a.

3. Скалярное произведение двух векторов равно 0 тогда и только тогда, когда сомножители ортогональны или хоть один из них равен 0.

4. Для любых векторов a, bиcи любых чисел α и β выполнимо равенство:

(αa + βb, c) = α(a , c) + β(b , c).

В частности (αa , c) = α(a , c); (a+b,c) = (a,c) + (b,c).

(без доказательства)

Пользуясь свойством 4, найдем выражение скалярного произведения двух векторов.

a= {α₁, α₂, α₃} иb = { β₁, β₂, β₃} в базисеe₁,e₂,e₃.

(a,b) = ({α₁e₁ + α₂e₂+ α₃e₃} , { β₁e₁+ β₂e₂+ β₃e₃} ) =

= α₁β₁ (e₁, e₁) + α₂β₂ (e₂, e₂) + α₃β₃ (e₃, e₃) +

+ ( α₁β₂ + α₂β₁)(e₁, e₂) + ( α₁β₃ + α₃β₁)(e₁, e₃) + (1)

+ ( α₂β₃ + α₃β₂)(e₂, e₃).

Определение:Базис называетсяортонормированным, если его векторы попарно перпендикулярны, и их длины равны 1.

Тогда (e₁, e₁) = (e₂, e₂) = (e₃, e₃) = 1.

и (e₁, e₂) = (e₁, e₃) = (e₂, e₃) = 0. (2)

Теорема: Если базис ортонормированный, то скалярное произведение векторов выражается через их компоненты по формуле:

(a , b) = α₁ β₁ + α₂ β₂ + α₃ β₃ . (3)

Доказательство: подставим (2) в (1)

Эта теорема позволяет написать выражение длины вектора через его компоненты (координаты) в ортонормированном базисе.

(4)

И выражение угла между векторами через их компоненты в ортонормированном базисе.

(5)

Определение:Декартова система координат, базис которой ортонормирован, называетсядекартовой прямоугольной системой координат.

Ортонормированный базис декартовой прямоугольной системы в трёхмерном линейном пространстве геометрических векторов обозначается обычно i,j,k. Оси координат обозначаютOX,OY,OZи называют соответственно ось абсцисс, ось ординат, и ось аппликат (см. рис.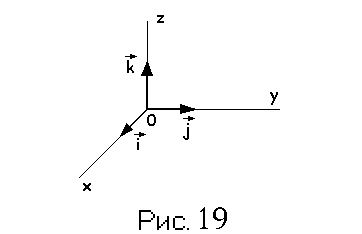19). Прямоугольные декартовы координаты векторов и точек обозначают буквамиx,y,z(В отличии от произвольных декартовых координат)

a = {x, y, z} и M(x, y, z)

Декартовы прямоугольные координаты очень широко применяются в задачах, связанных со скалярным произведением. Легко проверить (самостоятельно), что координаты точки в декартовой прямоугольной системе равны по абсолютной величине расстояниям до соответствующих координатных плоскостей. Они имеют знак “+” или “­–” в зависимости от того, лежит ли точка и базисный вектор, перпендикулярный этой плоскости, по одну сторону или по разные стороны от этой плоскости. На плоскости все аналогично, но более наглядно. Рассмотрим подробнее. (Рис 20)

Пусть M(x,y) – точка на плоскости. Её радиус векторOM= {x,y},

Т.е. OM=xi+yj. С другой стороныOM = OM_x + OM_y

Отсюда xi=OM_xx=|OM_x| / |i| =|OM_x|

(“+” – если OM_xиiнаправлены одинаково, “–” – если в противоположенные стороны).

Аналогично y=|OM_y|, ноOM_x = |OM|Cos(α) = пр_oxOM,

Т.е x= |OM|Cos(α) = пр_oxOM.

Аналогично OM_y= |OM|cos(β) = пр_oyOM,

Т.е. y= |OM|Cos(β) = пр_oyOM.

Углы α и β называются направляющими угламивектораOM, а их косинусы –направляющими косинусами. Из выше сказанного следует:

Cos(α) =x/ |OM|;Cos(β) =y/ |OM|

Формулы для направляющих косинусов остаются в силе и в пространстве и для произвольно расположенного вектора a= {x,y,z}:

Cos(α) =x/ |OM|;Cos(β) =y/ |OM|Cos() =z/ |OM|

Из формулы (4.8) следует, что расстояние между двумя точками A (x₁, y₁, z₁) иB(x₂, y₂, z₂) в декартовой прямоугольной системе вычисляется по формуле: