§17. Точки разрыва функции.

Определение. Если в точке х₀функция не является непрерывной, то точка х₀ называется точкой разрыва этой функции, а сама функция – разрывной в этой точке.

При этом предполагается, что в некоторой окрестности точки х₀ функция определена, в самой же точке х₀ она может быть как определена, так и нет.

Из определения следует, что разрыв в точке х₀ будет, если:

• или f(х₀)не существует, функция не определена в точке х₀,

• или не существует предел , т.е. не существуют односторонние пределы при хх₀, или они не равны между собой,

• или существует предел , но он не равенf(х₀).

Различают разрывы двух видов:

Разрывы I рода: односторонние пределы существуют, конечны, но:

а) либо не равны ;

б) либо равны между собой, но не равны значению функции f(х₀).

Вслучае а) предел называется сконечным скачком, в случае б) с устранимым разрывом.

Примеры:

1)в точке х=1 разрыв 1 рода с конечным скачком.,, 12, существуют, но не равны.

2. 2)имеет разрыв 1 рода в точке х=0.

3. 3) имеется устранимый разрыв в точке х=0. 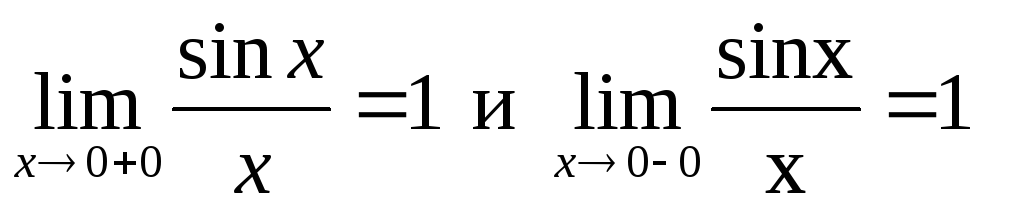. 1=1, но в точке х=0 функция не определена. Если доопределить функцию, положивf(0)=1, то функция станет непрерывной, разрыв устранится.

Остальные разрывы являются разрывами II рода: для них:

а) либо какай-то односторонний предел= (может и два),

б) либо не существует вовсе.

В случае а)разрыв называется иногда с бесконечным скачком,

Примеры:

1. x=0 – разрыв II рода с бесконечным скачком.

2. не существуют

x=0 разрыв II рода.

§18. Действия над непрерывными функциями.

Теорема 1. Если две функции f(х)и (х)определены в одном и том же промежутке Х и обе непрерывны в точке х₀, то в этой же точке будут непрерывны и функции:

1. f(х)(х)

2. f(х)(х)

3. если ((х₀)0)

Доказательство. Справедливость теоремы вытекает из справедливости соответствующих теорем о пределах функций.

Например:

1)т.к. f(х)и (х)непрерывны в точке х₀, то иНо тогда, т.е. предел функции при хх₀ равен значению функции в точке х₀, что и означает непрерывность функции f(х)(х)в точке х₀. Аналогично доказывается и остальное.

Замечание. Теорема верна, очевидно, и для любого конечного числа слагаемых, сомножителей. Теорема 1 позволяет, исходя из непрерывности простых функций, делать вывод о непрерывности более сложных.

Например:

1. , т.к. f(х)=x непрерывна в любой точке х₀, то и f(х)=хⁿ тоже.

2. непрерывны на всей прямой. Поэтому tgх непрерывен как частное везде, где cosx0, т.е. в области определения tg х.

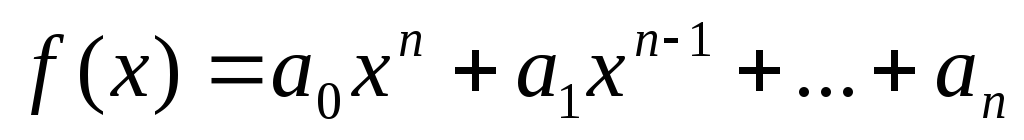3. непрерывна в любом х₀ как сумма непрерывных функций, а слагаемые непрерывны как произведения непрерывных.

Теорема 2. Сложная функция, составленная из конечного числа непрерывных функций, непрерывна (непрерывная от непрерывной есть функция непрерывная).

Доказательство. Проведем для двух звеньев (для большего числа аналогично). Пусть y=f(u)и u=(х)так, что y=f[(x)]=F(x), причем (х)непрерывна в точке х₀, f(u)непрерывна в точке u₀=(x₀). Следует показать, что функция y=f[(x)]=F(x)непрерывна как функция от х в точке х₀. Покажем: пусть хх₀, тогда по непрерывности u=(х) . Или при хх₀ uu₀. Но из непрерывности f(u) следует Или.

Предел функции при хх₀ равен значению функции в точке х₀, т.е. она непрерывна.

Теорема 3. Функция, обратная к возрастающей (убывающей) и непрерывной на некотором промежутке функции, существует и тоже является возрастающей (убывающей) и непрерывной.

Пример:

Функция является возрастающей и непрерывной в. Область ее значений (-,+). На промежутке (-,+), поэтому существует тоже возрастающая и непрерывная обратная функция y=arctgx.

Из приведенных теорем 1,2 следует, что т.к. основные элементарные функции непрерывны, то и любая элементарная функция, получаемая из основных элементарных при помощи 6 алгебраических операций и взятия функции от функции, есть функция непрерывная в своей области определения.

Точками разрыва элементарной функции могут быть лишь те значения аргумента х, при которых какие-либо из элементов, составляющих функцию, не определены, или обращаются в нуль знаменатели дробей, содержащихся в данной функции.

Способ нахождения предела функции при хх₀ подстановкой вместо х значений х₀ в выражение непрерывной функции особенно важен именно для элементарных функций, т.к. они наиболее часто встречаются на практике.

Пример: 1)

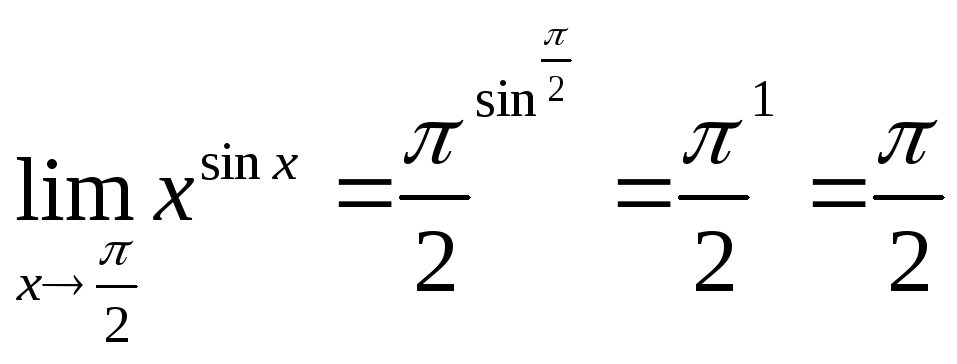
В общем виде: если u(х)^v(х)- непрерывная в точке х₀ функция (это когда u(x)и v(x)непрерывны в точке х₀),

то

2)