§14. Сравнение бесконечно малых величин.

Как и раньше мы будем говорить о б.м. функциях (х),(х),… от непрерывного аргумента, имея ввиду, что б.м.ф. от натурального аргумента (числовые последовательности) есть лишь частный случай и для них всё сказанное тем более верно.

Пусть имеется несколько б.м.в. (х), (х), (х),…, которые являются функциями одной переменной х, стремящейся к конечному или бесконечному пределу a (a – конечное число или ).

В ряде вопросов очень важно знать какая величина 0 быстрее. Например, (х)=1/x³ стремится быстрее к 0, чем (х)=1/x при x. В других случаях это увидеть сложнее.

Определение 1. Если двух б.м.(х) и (х) равен постоянному числу c0, то эти б.м.в. называются б.м. одного порядка (малости). Символически (х)=О((х)).

Пример:

(n) и (n) одного порядка малости sin1/2n=O(1/n).

Определение 2. Если двух б.м.в. равен нулю, то (х) называется б.м. высшего порядка (малости), чем (х), а (х) нижнего порядка малости, чем (х). Записывают (x)= o((x)).

Например: 1/x³=o(1/x),

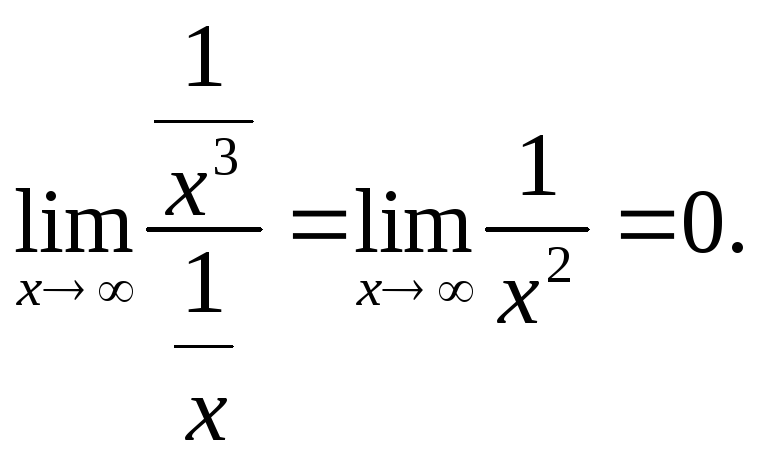
Определение 3. Если существует при ха бесконечный предел отношения (х)/(x), то (х)=о((х)). Если не существует при xa ни конечного, ни бесконечного предела отношения (х)/(x), то они называются несравнимыми.

Пример: (х)=хsin1/x,(x)=x, при х0 они б.м.в.,

т.к. (х)0 (б.м.в. на ограниченную)

(х)0.

Но 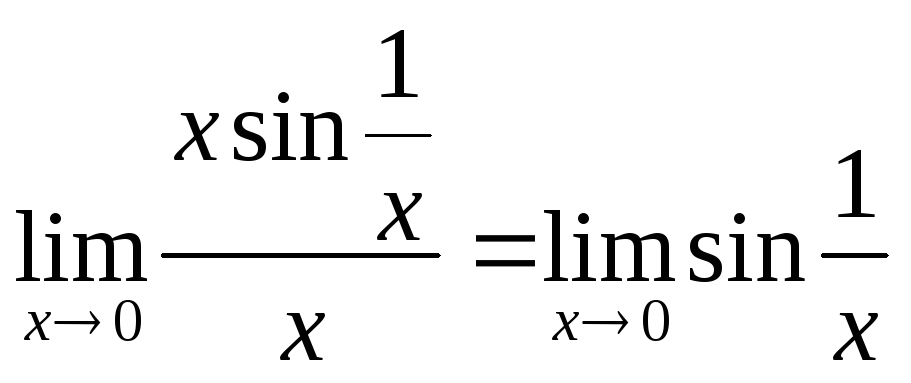не существует,(х) и (х) несравнимые б.м.в.

Бывает важно сравнить точно порядки малости сравниваемых б.м.в., выражая их числом.

Определение 4. (х) называется б.м. к-ого порядка по сравнению с б.м. (х), если (с – конечное число).

Пример. (x)=1/x³. (x)=1/x. => 1/x³ б.м. к=3 малости по сравнению с 1/x.

§15. Эквивалентные бесконечно малые величины.

Определение 5. Б.м.в. (х) и (х) называются эквивалентными б.м., если предел их отношения при ха равен 1, т.е.

Обозначим (х)(х). Например, sinx  x при х0, т.к.

Теорема. Для того, чтобы б.м.в. (х) и (х) были эквивалентными, необходимо и достаточно, чтобы их разность (х)=(х)-(х) была б.м.в. высшего порядка, чем (х) и чем (х).

Доказательство: I Н-ть. Пусть (х) (х), т.е. Тогда(х)=о((х)).Аналогично, показывается, что (х)=о((х)).

2. Достаточность. Пусть (х)-(х)=о((х)), т.е.

Тогда =>. ->(x) (x).

Приведем некоторые другие пары эквивалентных б.м.в. (все при х0), кроме sinx  x.

1. 

2. 

3. 

4. Положим y=e^x-1. Тогда при х0 и y0. е^х=y+1. х=ln(y+1). Тогда (Использован факт, что знак предела и непрерывной функции можно менять местами – будет доказано позднее).

5. /ч.т.д.

Из определения эквивалентных б.м.в. видно, что при х, достаточно близких к а, значения эквивалентных б.м.в. становятся сколь угодно близкими и их можно на практике заменить одна другой. Отсюда приближённые формулы. При малых х (близких к нулю) можем считать sinxx; ; tgxx, e^xx+1, ln(1+x)x и т.п. Ими с успехом пользуются в приближённых вычислениях.

Например.

1. 

(все цифры верные)

2. (в действительности 0,142)

Применяются эквивалентные б.м.в. и при вычислении пределов. Основой является:

Теорема. Если имеем две пары б.м.в. при х (х),(х), ₁(х),₁(х), причем (х)₁(х), (х)₁(х), то из существования предела следует существование пределаи их равенство.

Доказательство. Можем записать .

Тогда

Следствие. При нахождении пределов отношений б.м.в. каждую из них или обе сразу можно заменять эквивалентными им б.м.в., величина предела не изменится. Одну можно заменять потому, что можно считать ,. Тогда.

Пример.

Замечание. В общих пределах можно заменить на эквивалентные только б.м. сомножители, замена б.м. слагаемых может привести к ошибке.

Например.

Но нельзя так: - не имеет смысла.