§11. Число е.

Рассмотрим сначала переменную величину (n=1,2,…).

Теорема 1. Переменная величина приn имеет предел, заключенный между числами 2 и 3.

Доказательство. По формуле бинома Ньютона можем записать(1)

Преобразуем y_n, упростив его: (2)

Из выражения (2) видим, что y_n возрастает с возрастанием n (т.к. добавляются новые положительные слагаемые) и каждое слагаемое увеличивается, например, Поэтому для n y_n+1>y_n. Покажем, что переменная y_n ограничена сверху. Очевидно и т.д. Тогда из (2) можем записать.

Далее ; можем записатьy_n=

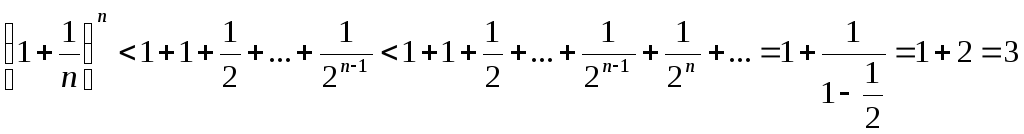
Итак, для любого n получаем, что (1+1/n)ⁿ<3, т.е. ограничена сверху. Но из (2) видно, что (1+1/n)ⁿ2. Таким образом, для всех n имеем неравенство

2(n+1/n)ⁿ<3. Так как величина (1+1/n)ⁿ – возрастающая и ограниченная сверху, то она имеет предел. Он не может быть больше 3-х и не может быть меньше 2-х. Этот предел обозначили числом е.

Он называется вторым замечательным пределом: 2е3.

е называют “числом Непера” (шотландский математик). Число е, как доказано, иррациональное. Вычислено его значение с многими десятками десятичных знаков. Приведем первые десять: е=2,7182818284...

Переменную величину (1+1/n)ⁿ можно рассматривать как функцию натурального аргумента: f(n)=(1+1/n)ⁿ. При n f(n)e. Рассмотрим функцию непрерывно меняющегося аргумента x: f(x)=(1+1/x)^x.

Теорема 2. Функция (1+1/x)^x при х стремится к числу е: .

Следствие. Предел функции при х0 равен числу е. Достаточно положить 1/х=у, тогда .

Примеры. 1)

Короче: .

3. .

§12. Понятие о гиперболических функциях.

Как увидим, число е играет важную роль в математике. В частности, важную роль играет показательная функция с основанием

е(экспонента):у=е^х. Она обладает обычными свойствами показательной функции (е>1). Но с помощью этой функции определяются, например, важные в применениях гиперболические функции. Функции эти определяются следующим образом:

1. гиперболический синус:

2. гиперболический косинус:

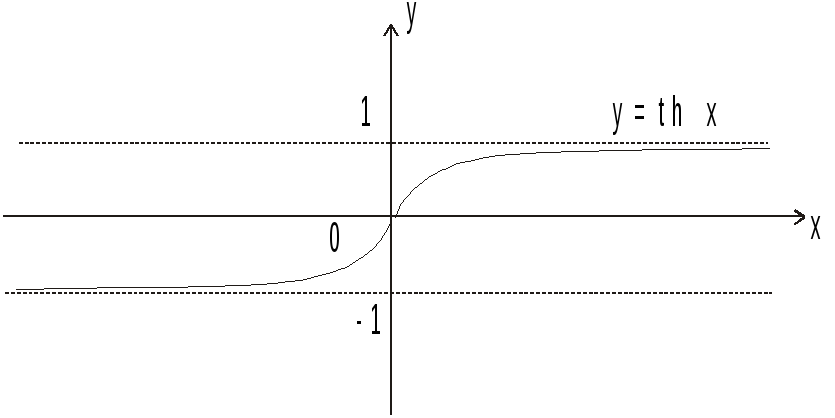
3. гиперболический тангенс:

4. гиперболический котангенс:

Функции получили название гиперболических, так как они удовлетворяют уравнению гиперболы х²-у²=1, т.е. Ch²x-Sh²x=1. (легко проверить подстановкой).

Обычные тригонометрические функции sin x и cos x называются круговыми, так как они удовлетворяют уравнению окружности х²+у²=1. Синусом, косинусом и т.д. они называются потому, что обладают многими свойствами тригонометрических функций.

Например:

1. thcthx=1

2. sh(x+y)=shxchx+shychy

3. ch(x+y)= chxchy+shxshy и т.п.

(проверяется подстановкой выражений через е).

Без подробных рассуждений приведем графики функций, учитывая, чтоshx, chx, tgx определены на (,+), а cthх во всех х0. Из графиков видны основные свойства функций.

§13. Натуральные логарифмы

Логарифмическая функция y=log_ax рассматривается при любом основании a>0, a1. Особо выделяют логарифмическую функцию с основанием a=10: y=log₁₀x=lgx. Такие логарифмы называются десятичными или Бригговыми (по имени английского ученого Бригга), они подробно изучались в школе. В математике и её приложениях очень часто применяются логарифмы с основанием a=e (числу Непера): y=log_ex=lnx. Они называются Неперовыми логарифмами или натуральными. (Непер тоже жил в 16 веке). Число y есть натуральный логарифм числа х: y=lnx, если e^y=x. lne=1, т.к. e¹=e. Графики натуральных и десятичных логарифмов имеют вид, обычный для логарифмической функции y=log_ax при a>1

Существует связь между десятичными и натуральными логарифмами одного и того же числа x>0. Установим её. Очевидно х=е^lnx. Прологарифмируем по основанию 10. lgx=lnxlge, т.к. е=2,7182818284…, то lge=0,434294. Число M=lge=

называется модулем перехода от натуральных логарифмов к десятичным.M не зависит от x lgx=Mlnx. Переход от десятичных к натуральным: . При этом 1/M2,302584. Для вычисления десятичных и натуральных логарифмов составлены подробные таблицы этих функций, которые содержатся в справочниках по математике.