§4. Свойства линейных операций.

Отметим восемь основных свойств линейных операций над векторами:

1. a+b=b+a (коммутативность сложения или переместительность)

2. a+(b+c)=(a+b)+c (ассоциативность сложения или сочетательность)

3. a+0=a.

4. Для любого вектора a существует ему противоположенный вектор –a, так что a+(–a)=0

5. 1a=a

6. m(na)=(mn)a (ассоциативность умножения на скаляр)

7. m(a+b)=ma+mb (распределительные свойства относи-

8. (m+n)a=ma+na тельно умножения на скаляр)

Справедливость свойств 3–5 для геометрических векторов очевидны. Справедливость свойств 1 и 2 следует из самого определения суммы двух векторов. (диагональ параллелограмма одна и та же для a+b и для b+a) (Рис. 11)

Свойство 6 и 8 следует из истолкования умножения вектора на скаляр m как "растяжения" его в |m| раз с возможным изменением направления на противоположенное. Свойство 7 следует из подобия треугольников. (Рис. 12)

§5. Разложение вектора по базису. Координаты вектора.

Рассмотрим систему n векторов а₁,а₂,а₃,…,а_n. Каждый вектор вида α₁а₁+α₂а₂+α₃а₃+…+α_nа_n , где α₁, α₂, α₃,…, α_n некоторые действительные числа, называется линейной комбинацией данных векторов, числа α₁, α₂, α₃,…, α_n называются коэффициентами этой линейной комбинации. Линейная комбинация называется нетривиальной, если хотя бы один коэффициент α_к  0 (в противном случае она называется тривиальной).

Если некоторый вектор d представить в виде определённой комбинации данных векторов. d=α₁а₁+α₂а₂+α₃а₃+…+α_nа_n то говорят, что вектор d разложен по системе векторов .

Теорема 1. Если e₁ и e₂ два неколлинеарных вектора, то всякий компланарный с ними третий вектор d раскладывается по ним и это разложение единственно.

Теорема 2. Если e₁,e₂,e₃ три некомпланарные вектора, то всякий четвертый ве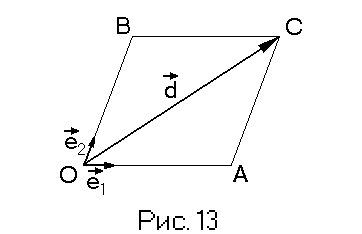кторd раскладывается по ним и это разложение единственно.

Доказательство теорем совершенно аналогично. Для краткости докажем теорему 1. Приведем вектора e₁, e₂ и d в одно начало О и построим параллелограмм, стороны которого лежат на векторах e₁, e₂, а вектор d является его диагональю. (Рис. 13)

Очевидно d=OC=OA+OB. Но OA || e₁ => OA=me₁, OB || e₂ => OB=ne₁. Тогда d=me₁+ne₂ – разложение получено и оно единственно, т.к. n и m определяются однозначно.

Определение: Любые два неколлинеарных упорядоченных (взятых в определенном порядке) вектора на плоскости называются базисом на этой плоскости.

Любые три некомпланарные упорядоченные вектора в пространстве называются базисом в пространстве.

Из сказанного выше следует (например, в пространстве), что задание базиса однозначно сопоставляет каждому вектору d тройку чисел {α, β, γ} – его коэффициенты разложения по этому базису, и наоборот: каждой упорядоченной тройке чисел {α, β, γ} при помощи базиса сопоставляется вполне определённый вектор d=αe₁+βe₂+γe₃ .

По этому введём:

Определение: Если вектора e₁,e₂,e₃ – базис и вектор а=αe₁+βe₂+γe₃ , то числа α, β, γ называются координатами (компонентами) вектора а в этом базисе.

Символически будем писать вектор а={α, β, γ}_(e1,e2,e3) или просто а={α, β, γ}.

Теорема 3. Над координатами векторов производятся те же линейные операции, что и над самими векторами.

Доказательство:

Пусть вектор а={α, β, γ}_(e1,e2,e3). Это означает а=αe₁+βe₂+γe₃.

Но тогда m а=m(αe₁+βe₂+γe₃) = (mα)e₁+(mβ)e₂+(mγ)e₃

Откуда следует, что вектор mа={mα, mβ, mγ}_(e1,e2,e3)

Пусть вектор b={α₁, β₁, γ₁} тогда

ab = (αe₁+βe₂+γe₃)  (α₁e₁+β₁e₂+γ₁e₃) =

= (αα₁)e₁+(ββ₁)e₂+(γγ₁)e₃

отсюда следует, что ab = {αα₁, ββ₁, γγ₁}.