§7.Основные теоремы о действиях над пределами

Будем по-прежнему говорить о хх₀, хотя все верно и для х.

Теорема 1.

Предел алгебраической суммы нескольких функций, имеющих конечные пределы, равен алгебраической сумме пределов этих функций:

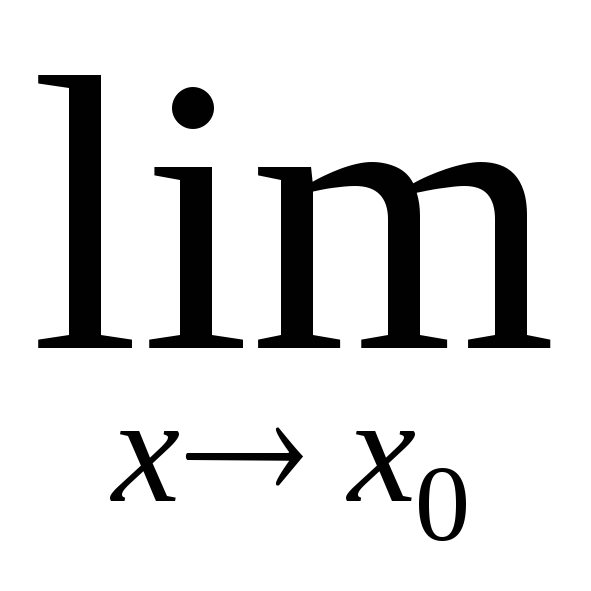(f₁(x)f₂(x)...f_n(x))= f₁(x)...f_n(x).

Доказательство.

Приведем для 2–х. Пусть f₁(x)=А₁, f₂(x)=А₂. Тогда по теореме 4 f₁(x)=А₁+_х и f₂(x)=А₂+₂х-₁(х) и ₂(х)- б.м.в. при хх₀.

Но тогда f₁(x)f₂(x)=А₁А₂+_х₂х отсюда (f₁(x)f₂(x))= = А₁А₂ = f₁(x)f₂(x).

Пример.

= (1+)= 1 + =1+0=1.

Теорема 2.

Предел произведения нескольких функций, имеющих конечные пределы, равен произведению пределов этих функций:

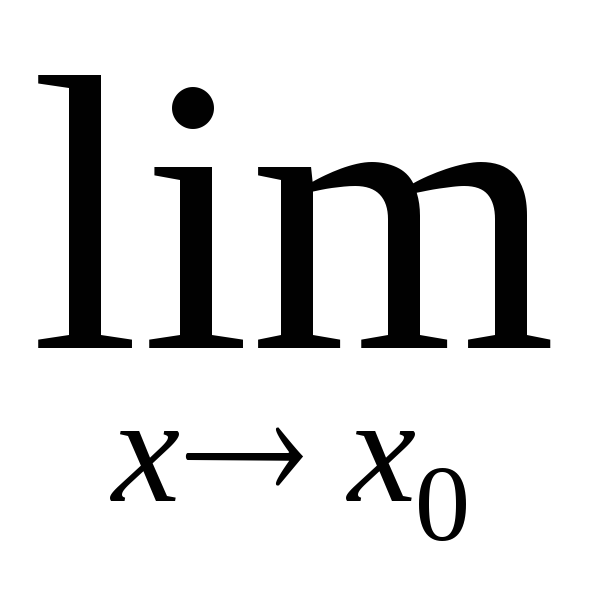(f₁(x)f₂(x)...f_n(x))= f₁(x)... f_n(x).

Доказательство. (для 2-ух).

Пусть f₁(x)=А₁, f₂(x)=А₂. Тогда по теореме 4 f₁(x)=А₁+_х и f₂(x)=А₂+₂х.

. По теореме 4

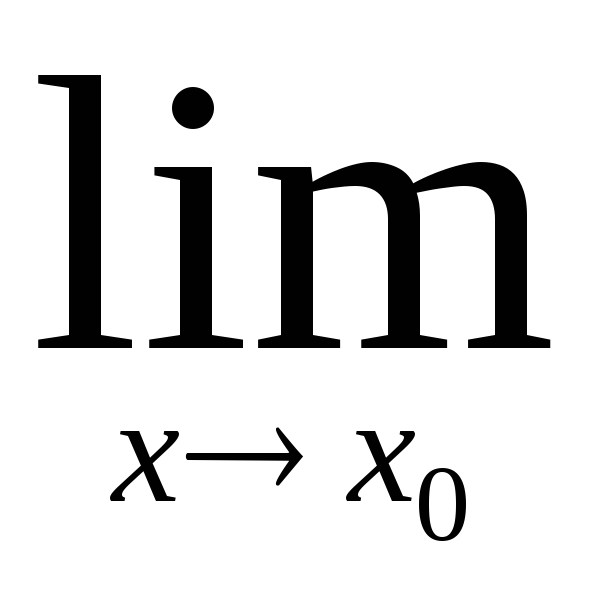f₁(x)*f₂(x)=А₁*А₂ ч.т.д.

Следствие. Постоянный множитель можно выносить за знак предела С*f(x)=С*f(x)

Доказательство.

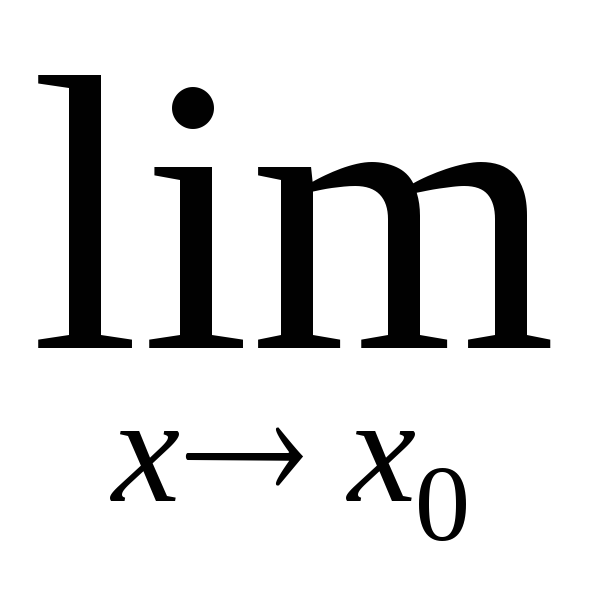С = С. По теореме 2 все сразу следует.

Пример.

3х² = 3х²= 3*2²=3*4=12.

Теорема 3.

Предел частного двух функций, имеющих конечные пределы, равен частному их пределов, если предел знаменателя не равен нулю: f₁(x)/f₂(x)= f₁(x)/ 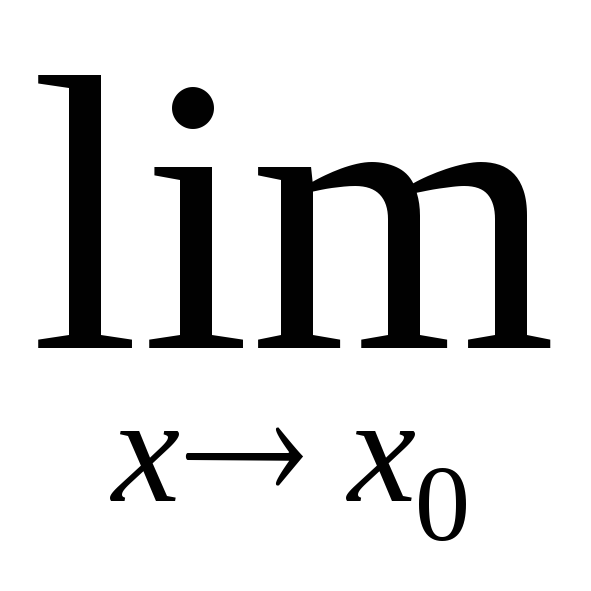f₂(x).

Доказательство.

Пусть f₁(x)=А₁, 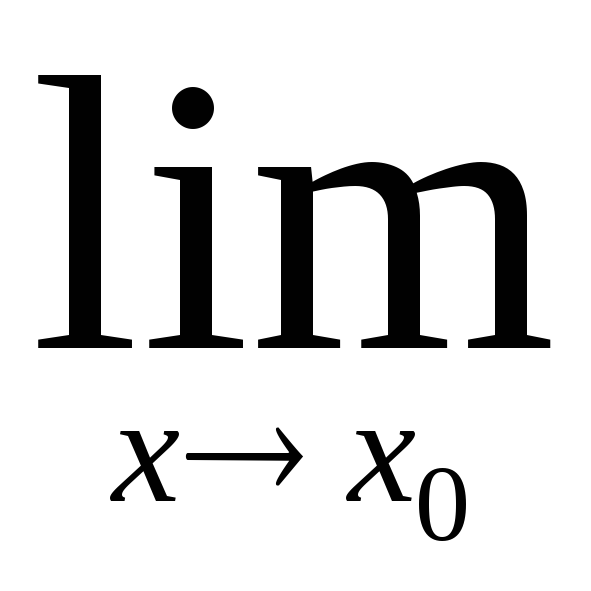f₂(x)=А₂0. Тогда f₁(x)=А₁+₁x, f₂(x)=А₂+₂х.

- число, а второе слагаемое б.м.в., т.к. в знаменателе стоит величина, имеющая пределом А₂². Но тогда - конечное число. Произведение б.м.в. в числителе на величину, имеющую предел, есть б.м.в. Но тогда .

Замечание.

Т.к. числовая последовательность {x_n} может считаться функцией от натурального аргумента n

х_n = f(n):x₁ = f(1), x₂ = f(2), то все теоремы о пределах функций верны и для числовых последовательностей. Пир этом n, и только:

1. lim(x_ny_n)=lim x_n  lim y_n

2. lim(x_ny_n)=lim x_nlim y_n

3. lim(x_n/y_n)=lim x_n/lim y_n

lim c*x_n=c lim x_n

Пример.

§8.Неопределенные выражения

В рассмотренных теоремах о пределах речь шла о существовании конечных пределов слагаемых, сомножителей, числителей и знаменателей( причем знаменатель не равен нулю).

В случае несоблюдения этих требований, теоремы уже неприменимы, и сказать сразу о существовании предела и тем более его величине для таких выражений нельзя. Такие выражения называют неопределенными (или неопределенностями). Исходя из теорем можно сделать вывод о существовании четырех видов неопределенностей:

, , 0, -.

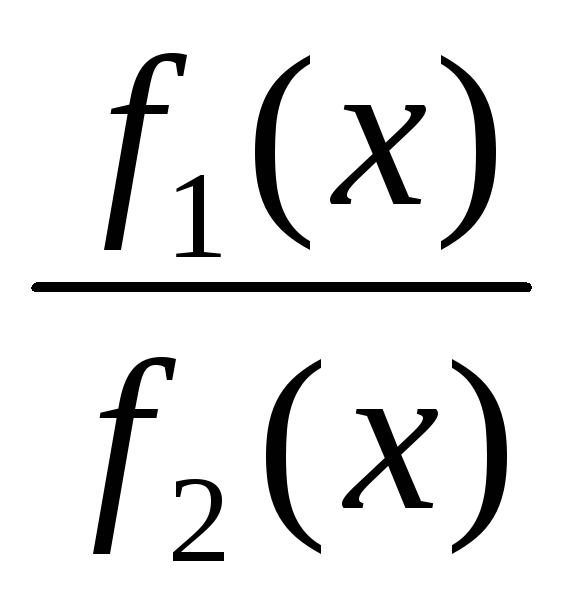1. - это неопределенность , когдаf₁(х)0 и f₂(х)0

при хх₀. может быть б.м.в., б.б.в., иметь предел0 или вообще не иметь никакого предела.

Например, , при х0 это б.б.в., б.м.в., и т.п.

2. - это неопределенность , когда f₁(х) и f₂(х), для может быть любой из четырех случаев.

3. 0 - это неопределенность f₁(х)f₂(х), когда f₁(х)0, а f₂(х). Для f₁(х)f₂(х) может быть тоже четыре вида.

4. - - это неопределенность f₁(х)- f₂(х), когда f₁(х)+, f₂(х)+. Для f₁(х)- f₂(х) может быть четыре вида.

Т.к. теоремы о пределах в этих случаях неприменимы, то исходя из конкретного вида переменных в каждом отдельном примере, проводят преобразования, позволяющие найти предел. (Эти преобразования называются раскрытием неопределенности).

Примеры: 1.)

1.