§4. Бесконечные пределы функции.

БЕСКОНЕЧНО БОЛЬШИЕ ВЕЛИЧИНЫ.

До сих пор мы считали, что А – это некоторое число. Полезно обобщить понятие предела на тот случай, когда функция неограниченно возрастает по абсолютной величине.

Определение.

Функция f(х) при хх₀ имеет пределом  (стремиться к бесконечности), если для любого наперед заданного числа М0 (сколь угодно большого) можно найти 0, что для всех хх₀ и удовлетворяет неравенству хх₀ выполняется неравенство f(х).

Символически записывается так: f(х)= или f(х) при хх₀.

Если f(х) при хх₀ и принимает только положительные или только отрицательные значения, то соответственно пишут f(х)=+ или f(х)=-.

При этом определение дословно аналогичное, только должно выполняться неравенство f(х), или f(х)-.

Геометрически это означает, что каким бы большим ни было число М0, найдется - окрестность точки х₀, для всех точек которой график функции расположен выше прямой у= М и ниже у=-М.

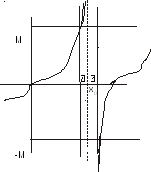
Пример

у=1/х², при х у=f(х). Возьмем любое М, должно выполняться 1/х²М, х²1/М, хММ. Например М=4, .

Нетрудно дать и определение  предела функции при х. f(х)=: если для любого М можно указать Р, что из хf(х).

Самим дать определение f(х)=, f(х)=, f(х)=- и т.п.

Определение.

Функция f(х) называется бесконечно большой величиной (б.б.в.) при хх₀ или х, если она стремится к бесконечности.

Так, 1/х²- бесконечно большая величина при х0. Следует не смешивать понятия б.б.в. и очень большого числа . Б.б.в.- это переменная величина.

Замечание:

Функция у=f(х) при хх₀ или х может не иметь ни конечного ни бесконечного предела.

Например: у=sin 1/х, при х она не имеет предела;

у=cosх, при х - не имеет предела.

§5.Ограниченные функции

Функция у=f(х) называется ограниченной в некоторой области определения Х, если существует такое число К0, что для любого хХ выполняется неравенство f(х)К. Если такого К не существует, то функция называется неограниченной в Х.

Очевидно б.б.в. при хх₀ являются неограниченными в окрестности точки х₀. Справедлива теорема.

Теорема.

Если существует конечный предел 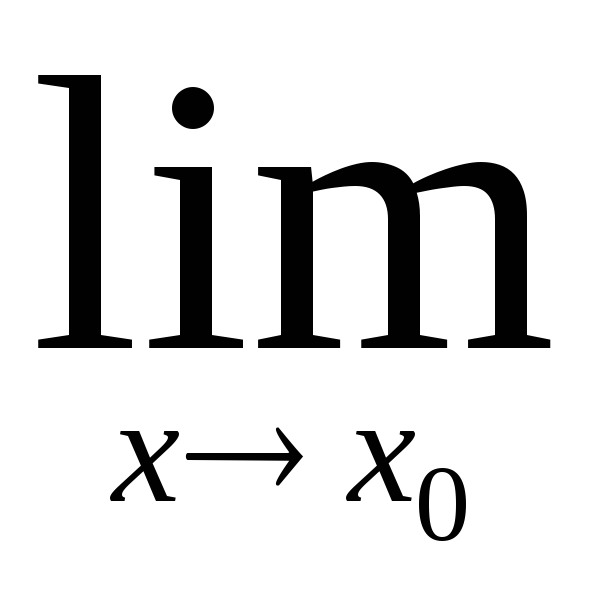f(х)=А, то в некоторой окрестности точки х₀ функция у=f(х)- ограничена.

Доказательство.

Пусть 0 любое число, тогда найдется , что для любого хх₀х₀,f(х)-А или f(х) f(х)-А  |f(х)| , (=К). Это и означает ограниченность f(х) в х₀х₀.

Обратная теорема неверна. Так функция у=sin1/х ограничена в окрестности 0, но предела при х0 не имеет.

§6.Бесконечно малые величины (б.М.В.) и их основные свойства

Определение. Функция, имеющая пределом 0 при хх₀ (x) называется бесконечно малой величиной, или просто бесконечно малой при хх₀ (x).

Обычно б.м.в. обозначают символами (х), (х),(х) и т.д.

Из определения следует, что (х)есть б.м.в. при хx₀, если для любого  найдется  такое ,что дляхх₀х.

Пример:

функция (х)=х² есть б.м.в. при х0, т.к х²=0.

функция (х)=sinх есть б.м.в. при х0, х; (х)=log_ах при х1 и т.п.

Замечание.

Не следует смешивать б.м.в. и очень малое число. Только число 0 считается б.м.в. так как 0=0. В дальнейшем говорим о пределах при хх₀ ,хотя все верно и для х.

Теорема 1 .

Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.

Доказательство.

Пусть ₁(х),₂(х),..._n(х)- б.м.в. при хх0.

Докажем ,что (х)= ₁(х)+...+ _n(х)- б.м.в.

Возьмем любое . Найдем _, что для х-x₀_ _хn;

Найдем ₂ что для х-x₀_i, ₂хn_;

Найдем _n, что для х-x₀_n_nхn;

Возьмем =min{₁,,_n}.

Тогда для этого любого  при  из х-x₀ одновременное выполнение всех неравенств.

Но тогда х_х+_nх_х_nх/n+...+/n=n/n=, т.е. x что и требовалось доказать.

Замечание: для случая бесконечного числа б.м.в. теорема может быть не верна. Например:

(х)=1/х+...+1/х (х-раз.), 1/х- есть б.м.в. при х, а х=1, и, т.е. не является б.м.

Теорема 2.

Произведение б.м.в. (х) при хх₀ или х на функцию, ограниченную в окрестности точки х₀ () есть величина б.м.

Доказательство. Пусть (х) б.м.в. при хх₀ и в некоторой окрестности х₀-₁ х₀+₁ функция f(х) ограничена, т.е. f(х) для всех х из этой окрестности. Но так как (х)=0 , то для любого  найдется _, что для х х-х₀₂, т.е. для xх₀-₂ х_₂ выполняется f(х)/К. Выберем min₁₂тогда для х, удовлетворяющего неравенству х-х₀, выполняются оба неравенства, и потому хf(х). Но это и значит, что хf(х)- б.м.в. при хх₀.

Следствие 1. Произведение б.м.в. на постоянную есть б.м.в.(при хх₀).

Следствие 2. Произведение б.м.в. на величину, имеющую предел, есть б.м.в. (при хх₀).

Следствие 3.Произведенеие нескольких б.м.в. есть б.м.в. (при хх₀).

Следствие 4.Целая положительная степень б.м.в. есть б.м.в.

Теорема 3.( о связи б.м.в. и б.б.в.)

Если величина х б.м. при хх₀ (и не обращается в нуль), то обратная ей величина 1/(х) есть б.б.в.

Доказательство.

Возьмем любое М0 и считаем =1/М. Тогда т.к. (х)0 при хх₀, то для =1/М0 найдется 0, что для х-х₀ выполняется неравенство (х)1/М, или для тех же х-х₀. 1/(х)М, что и означает, что 1/(х) при хх₀, т.е. 1/(х) б.б.в.

Верно и обратное: если f(х) – б.б.в. при хх₀ и f(х) не обращается в 0, то 1/f(х) – б.м.в. при хх₀.

Т.к. f(х) б.б.в., то для любого 0 найдется 0, что для х-х₀ f(х)1/ 1/f(х) для тех же х, ч.т.д.

Например. х²0 при х0. 1/х² при х0.

Теорема 4. (о связи предела и б.м.в.)

Функцию у=f(х), имеющую пределом число А при хх₀ или х, можно представить в виде суммы этого числа и некоторой б.м.в.: f(x)=А+х.

Обратно, если функцию у=f(х) можно представить в виде суммы некоторого числа А и некоторой бесконечно малой х, то А есть предел функции: f(x)=А.

Доказательство.

1) Пусть lim_ f(x)=А. Это значит, что для любого 0 найдется  , что для ххх₀ будет f(x)-А. Обозначим f(x)-А=х, тогда х, а это означает что х б.м.в. Откуда f(x)=А+х и х при хх₀.

2) Наоборот.

Пусть f(x)=А+х и х при хх₀. Тогда для любого  найдется , что из хх₀ следует х или f(x)-A. А это и означает, что f(x)=А.