§10. Элементарные функции.

Среди большого числа различных функций в математическом анализе особо выделяют класс элементарных функций. Это класс функций, которые конструируются из простейших элементарных (или основных элементарных), а также постоянных с помощью конечного числа операций сложения, вычитания, умножения, деления, возведения в степень, извлечения корней и взятия функций от функций. Элементарные функции задаются аналитически.

К основным элементарным функциям относятся:

1) Степенная функция: у=х^ (-действительное число);

2) Показательная функция: у=а^х (а1, а0 - действительное число).

3) Логарифмическая функция: у=log_ах, где основание а0, а1 - действительное число.

4) Тригонометрические функция: у=sinx, y=cosx, y=tgx, y=ctgx, иногда у=secx=1/cosx, y=cosecx=1/sinx.

5) Обратные тригонометрические функции: y=arcsinx, y=arccosx , y=arctgx, y=arcctgx, y=arcsecx, y=arccosecx.

Рассмотрим области определения и графики основных элементарных функций.

1) Степенная у=x^.

1. =n - натуральное число, у=хⁿ - парабола, X;

2. =-n - целое отрицательное, у=х^-n, X - гипербола;

в) =m/n- дробное положительное, у=х^m/n=ⁿ - область определения и график зависит от четности и нечетности m и n.

Так , y=³х²,  у;

, y=х³, , y;

 y=⁵Х³, , y-любое.

2.Логарифмическая функция

у=log_ах, , a, a1

а - возрастает,

а - убывает,

3.Показательная функция

у=а^х, , а- возрастает, а- убывает,

4.Тригонометрические

у=sinx, y=cosx, 

y=tgx, xk

y=ctgx, xk;

5.Обратные тригонометрические

y=arcsinx, х=, y=arccos x ,х= y=arctgx,х=( y=arcctgx.

Примерами элементарных функций могут служить и т.д.

Важными примерами элементарных функций являются:

1. Целая рациональная или многочлен:

у=а₀хⁿ+а₁х^n-1+...+а_n(a₀,a₁,…,a_n - любые д.ч., коэффициенты, n-степень). Область определения: .

Частными случаями являются:

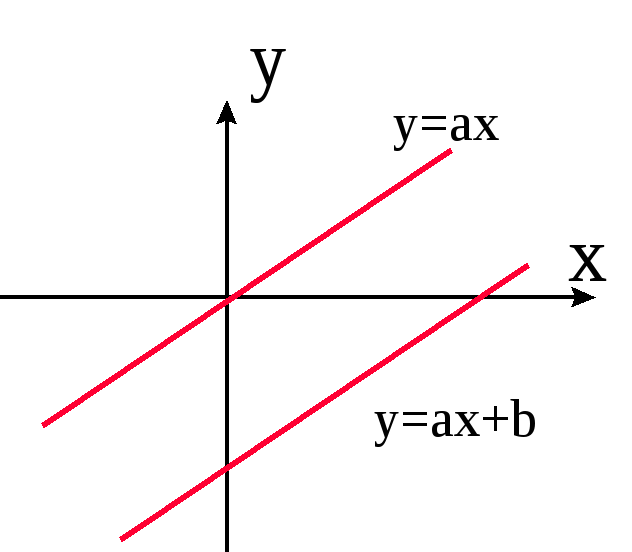
1) у=ах+b - линейная функция. /При b=0, у=ах – прямая пропорциональная зависимость у от x. При а=0, у=b - постоянная. График есть прямая || OX/. Можно построить у=ах (проходит через начало) и поднять или опустить на b по оси ординат.

2) у=ах²+вх+с - квадратичная функция. Определена для любого х. График есть парабола. При а>0 ветви направлены вверх, при а<0 - вниз. Если уравнение у=ах²+вх+с=0 имеет два действительных корня х₁ и х₂, то парабола пересекает ось OX в точках х=х₁ и х=х₂, если корни действительны и равны, то касается оси OX в точке х=х₁=х₂. Если корни мнимые, то не пересекает ось OX, расположена выше или ниже оси OX.

2.) Дробно-рациональная.

- отношение двух многочленов.

Частным случаем является дробно-линейная, (а,b,с,d - числа, с - не равно нулю). Область определения все х-d/c. Если а=0, d=0, то имеем - обратная пропорциональная зависимость, график - гипербола с осями в качестве асимптот. В общем случае графиком дробно-линейной функции является тоже гипербола, асимптотами которой являются прямые х=-d/с, и у=а/с.

Например:

, а=1, b=1, с=1, d=-1,

х=-d/с=1, у=1.

Есть и другие виды элементарных функций. Например, иррациональные (содержат аргумент под корнем).

Рациональные и иррациональные образуют множество алгебраических функций. Элементарные функции, не являющиеся алгебраическими, называются трансцендентными: у=sinx, y=а^х, и т.п.