§7. Обратная функция и ее график.

Пусть имеется функция у=f(x), Х - ее область определения, Y - область значений. Мы знаем, что каждому х₀ соответствует единственное значение у₀=f(х₀), у₀Y.

Может оказаться, что каждому у (или ее части ₁) соответствует тоже единственное х из Х.

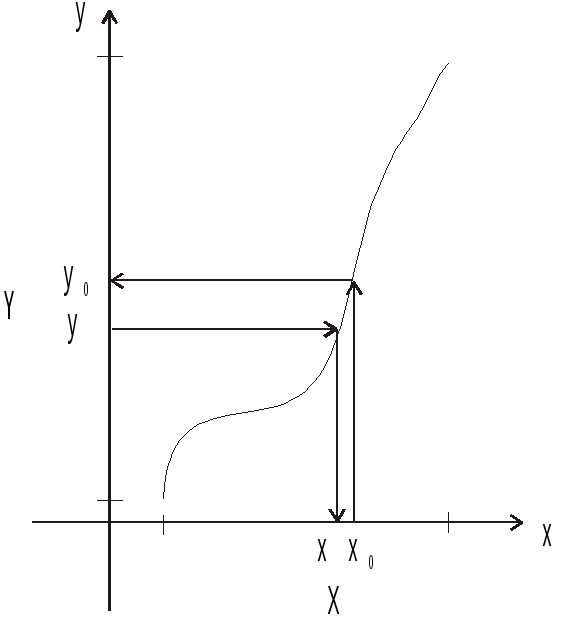
Тогда говорят, что на области  (или ее части _) определена функция x=y обратная для функции у=f(x).

Например:

1. у=х³. X Y, обратная функция , область определенияY, область значений X

2. y=x².

X=(); Y=[0)

x= – однозначной обратной функции нет: каждому y соответствуют два значения x. Если же рассмотреть y=x² с областью определения X₁=[0); Y=[0), то ей существует обратная x=+√y область определения Y=[0), область изменения X=[0).

Графики прямой и обратной функции совпадают, очевидно. Но принято обычно аргумент обозначать через х, а функцию через у. Поэтому обратные функции записались бы так: yy. Графики этих функций остались такими же линиями, если бы переобозначить оси координат. Но это тоже не делают, ось ОХ всегда горизонтальна. Поэтому график обратной функции можно получить либо по точкам, либо отобразив его зеркально относительно биссектрисы 1 и 3-го квадрантов, т.к. переобозначение координат на точки биссектрисы не влияет.

§8. Понятие сложной функции (функции от функции).

Пусть переменная y есть функция от переменной u: y=F(u), а переменная u есть сама функция от переменной x u=(x). Тогда y тоже зависит от x. Пусть функция u=(x) определена на X и область её значений U, функция y=F(u) определена либо на всей U (либо на её части U, U). Тогда каждому xX соответствует единственное uU, а этому u соответствует единственное yY. Тем самым на X определена функция - которая называется сложной функцией или функцией от функции. При этом x – независимая переменная (аргумент), u – промежуточная переменная, y - функция.

Пример:

у=sinх² - это сложная функция: у=sinu, u=х².

Сложная функция может образовываться и более чем из двух звеньев. Так . Тут у=u, u=tgv, v=х²+1.

Задание сложной функции называется еще цепным заданием.

§9. Основные характеристики поведения функции.

Для изучения функции у=f(x) бывает полезно исследовать ее на четность, на периодичность, на монотонность. Дадим соответствующие определения, будем полагать, что значения аргумента x изменяются, возрастая и принимая все промежуточные значения.

Определение 1.

Функция у=f(x) называется четной, если при изменении знака y любого значения аргумента, значение функции не изменится f(-x)=f(x). Функция называется нечетной, если при изменении знака у любого значения аргумента изменяется только знак значения функции, а абсолютная величина значения остается прежней f(-x)=-f(x).

Заметим, что функция полагается определенной на симметричном относительно начала координат промежутке.

Например, у=х², у=cosx - четные, у=х³, у=sinх - нечетные.

Графики четных функции симметричны относительно осиOY, нечетных - симметричны относительно начала координат. Ясно, что бывают функции ни четные, ни нечетные: (у=2^x).

Определение 2.

Функция у=f(х) называется периодической, если существует такое положительное число l, что для любого x справедливо равенство f(x+l)=f(x) (1).

Если функция периодическая, то верны и равенства f(x+2l)=f(x), f(x-3l)=f(x) и вообще f(x+kl)=f(x) (к - любое целое число). Наименьшее число l, при котором выполняется равенство (1), называется периодом функции у=f(x).

Например.

у=sinx, y=cosx имеют период l=2, y=tgx, y=ctgx имеет l=.

График периодической функции повторяется, поэтому достаточно вычертить его в промежутке длиной в 1 период l.

Определение 3.

Функция называется возрастающей в некотором интервале, если любому большему значению аргумента соответствует большее значение функции. Функция называется убывающей на интервале, если любому большему значению аргумента соответствует меньшее значение функции.

Таким образом, если х₁, х₂ любые значения из (а, b) и ах₁х₂b, то f(x₁)f(x₂) - в случае возрастающей функции и f(x₁)f(x₂) - в случае убывающей.

Так у=2^х возрастает, а - убывает в. Интервал (а,b) называется интервалом возрастания или убывания функции или интервалом монотонности.