
- •Кафедра математического анализа в.А. Байков
- •Математика
- •Содержание
- •§1. Скалярные и векторные величины. 5
- •§2. Коллинеарные, равные, компланарные векторы.
- •§3. Линейные операции над векторами.
- •§4. Свойства линейных операций.
- •§5. Разложение вектора по базису. Координаты вектора.
- •§6. Линейная зависимость векторов.
- •§7. Декартова система координат.
- •§8. Линейные пространства.
- •§9. Скалярное произведение векторов.
- •§10. Евклидово пространство.
- •Углом между векторами xиyназывается каждое число, удовлетворяющее условию:
- •§11. Векторное произведение двух векторов.
- •§12. Смешанное произведение трех векторов.
- •2. Прямая линия и плоскость
- •§1. Понятие уравнения линии и поверхности.
- •§2. Уравнения плоскости, уравнения прямой на плоскости и в пространстве.
- •§3. Условия параллельности и перпендикулярности прямых и плоскостей.
- •§4 Основные задачи о прямых и плоскостях.
- •3. Кривые второго порядка
- •4. Матрицы и их применение
- •§1. Основные определения. Действия над матрицами
- •§2. Понятие ранга матрицы
- •§3. Понятие об обратной матрице
- •§4. Решение систем линейных уравнений с помощью обратной матрицы
- •§5. Решение систем линейных уравнений методом исключения неизвестных (метод Гаусса)
- •§6. Линейные преобразования на плоскости и в пространстве
- •§7. Собственные векторы и собственные числа матрицы (линейного преобразования)
- •§8. Собственные числа и собственные векторы в случае симметрической матрицы
- •§9. Приведение квадратичной формы к каноническому виду
- •§10. Приведение общего уравнения второго порядка к каноническому виду
- •5. Поверхности второго порядка
- •§1. Порядок поверхности.
- •§2. Цилиндрические поверхности с образующими, параллельными одной из координатных осей.
- •§3. Уравнение поверхности вращения.
- •§4. Сжатие и растяжение поверхностей.
- •§5. Эллипсоид
- •§6. Однополостный гиперболоид.
- •§7. Двухполостный гиперболоид.
- •§8. Конус.
- •§9. Эллиптический параболоид.
- •§10. Гиперболический параболоид.
- •II.Введение в математический анализ.
- •§2. Абслютная величина действительного числа и её свойства
- •§3. Переменные и постоянные величины.
- •§4. Область изменения переменной величины.
- •§5. Понятие функции.
- •§6. Способы задания функции.
- •§7. Обратная функция и ее график.
- •§8. Понятие сложной функции (функции от функции).
- •§9. Основные характеристики поведения функции.
- •Определение 1.
- •§10. Элементарные функции.
- •§11. Некоторые приемы построения графиков функций.
- •§1.Упорядоченная переменная величина.
- •§2. Предел переменной величины.
- •§3. Предел функции.
- •§4. Бесконечные пределы функции.
- •§5.Ограниченные функции
- •§6.Бесконечно малые величины (б.М.В.) и их основные свойства
- •§7.Основные теоремы о действиях над пределами
- •§8.Неопределенные выражения
- •§9. Другие свойства пределов.
- •§10. Предел функции при х0 (х – радианная мера угла).
- •§11. Число е.
- •§12. Понятие о гиперболических функциях.
- •§13. Натуральные логарифмы
- •§14. Сравнение бесконечно малых величин.
- •§15. Эквивалентные бесконечно малые величины.
- •§16. Непрерывность функции в точке и в промежутке.
- •§17. Точки разрыва функции.
- •§18. Действия над непрерывными функциями.
- •§19. Свойства функций, непрерывных на сегменте
§4. Сжатие и растяжение поверхностей.
Пусть
имеем некоторую поверхность ![]() , F(x,y,z)=0
(1)- её уравнение. Возьмём какое-либо
положительное число к>0 и заменим
каждую точку
, F(x,y,z)=0
(1)- её уравнение. Возьмём какое-либо
положительное число к>0 и заменим
каждую точку ![]() поверхности
поверхности ![]() другой точкой М(х,у,z)
причём,
другой точкой М(х,у,z)
причём,
![]()
![]() ,
,![]() ,
,![]() .
.

Тогда
поверхность ![]() преобразуется в новую поверхность S.
Очевидно, при к>1 имеем растяжение в
направлениях оси OZ , в случае k<1
-сжатие по той же оси.
преобразуется в новую поверхность S.
Очевидно, при к>1 имеем растяжение в
направлениях оси OZ , в случае k<1
-сжатие по той же оси. ![]() Точка
Точка ![]() лежит на поверхности
лежит на поверхности ![]() .
.
Поэтому
![]() или
или ![]() (2) .
Уравнению (2) удовлетворяет координаты
любой точки М на S.
Значит, (2) и есть уравнение «растянутой»
по оси OZ поверхности S.
(2) .
Уравнению (2) удовлетворяет координаты
любой точки М на S.
Значит, (2) и есть уравнение «растянутой»
по оси OZ поверхности S.
Итак,
правило:
Чтобы получить уравнение «растянутой»
в k
раз по оси OZ поверхности S
, нужно в уравнении исходной поверхности
заменить z
на ![]() .
.
Рассмотрим теперь другие (не цилиндрические) часто встречающиеся поверхности 2го порядка.
§5. Эллипсоид
Будем
вращать эллипс  вокруг оси OZ. Получим поверхность
вокруг оси OZ. Получим поверхность  (1) , которая называется эллипсоидом
вращения. Если
растянуть эллипсоид по оси OX в к раз, то
в уравнение (1) координаты х заменятся
на
(1) , которая называется эллипсоидом
вращения. Если
растянуть эллипсоид по оси OX в к раз, то
в уравнение (1) координаты х заменятся
на ![]() и мы получим
и мы получим  .
Положив
.
Положив ![]() мы получим каноническое
уравнение эллипсоида общего
вида.
мы получим каноническое
уравнение эллипсоида общего
вида.  .(2)
.(2)
Если рассекать эллипсоид какой либо плоскостью, параллельной одной из координатных плоскостей, то получим эллипс.
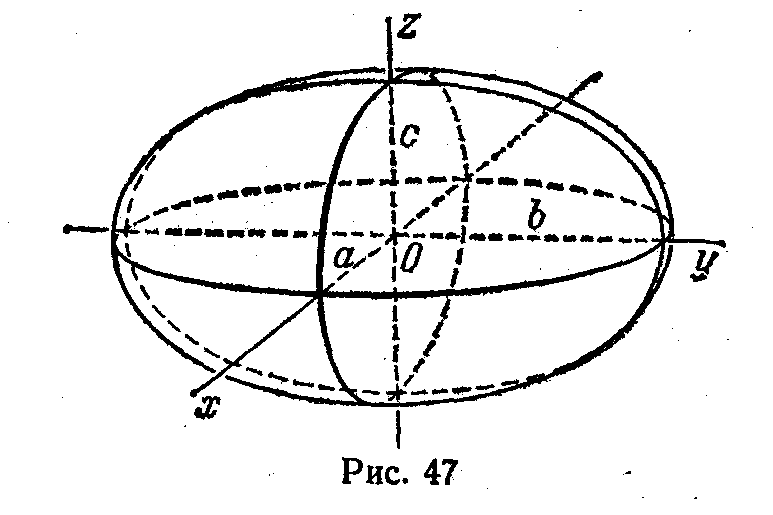 Например,
пологая z=h,
-c<h<c,
получим в сечении эллипс
Например,
пологая z=h,
-c<h<c,
получим в сечении эллипс  или, если разделить обе части на
или, если разделить обе части на ![]() и положить
и положить  ,
, , то получим
, то получим  .
Аналогично, пологая x=h
или y=h,
получим тоже эллипсы. Этим и объясняется
название поверхности - эллипсоид. Числа
a,b,c
называются полуосями
эллипсоида.
Если они различны, то эллипс называют
трёхосным.
Эллипс (1) будет двуосным.
Сфера, очевидно, есть частный случай
эллипсоида, когда a=b=c=R.
.
Аналогично, пологая x=h
или y=h,
получим тоже эллипсы. Этим и объясняется
название поверхности - эллипсоид. Числа
a,b,c
называются полуосями
эллипсоида.
Если они различны, то эллипс называют
трёхосным.
Эллипс (1) будет двуосным.
Сфера, очевидно, есть частный случай
эллипсоида, когда a=b=c=R.
Замечание. Первоначальный эллипс можно вращать и около оси OY. Получим тоже эллипсоид. Он называется вытянутым, а от вращения около оси OZ - сжатым.
§6. Однополостный гиперболоид.
Если
вращать гиперболу  вокруг оси OZ,
то в результате получим поверхность
вокруг оси OZ,
то в результате получим поверхность  (1), она называется однополостным
гиперболоидом вращения.
Растянем этот гиперболоид по оси ОХ в
к раз тогда х заменим на
(1), она называется однополостным
гиперболоидом вращения.
Растянем этот гиперболоид по оси ОХ в
к раз тогда х заменим на ![]() .
Обозначим
.
Обозначим ![]() .
В результате получим каноническое
уравнение однополостного
гиперболоида
общего вида.
.
В результате получим каноническое
уравнение однополостного
гиперболоида
общего вида. (2). Если рассекать однополостный
гиперболоид плоскостями параллельными
плоскости XOY,
их уравнение z=h,
то в сечении получим эллипсы:
(2). Если рассекать однополостный
гиперболоид плоскостями параллельными
плоскости XOY,
их уравнение z=h,
то в сечении получим эллипсы:  или
или  (3), где
(3), где  ,
,
 .
Самый малый эллипс будет с полуосями a
и b
при z=0
:
.
Самый малый эллипс будет с полуосями a
и b
при z=0
:  - так называемый горловой
эллипс. При
сечении плоскостями x=h
и y=h
получаем гиперболы
- так называемый горловой
эллипс. При
сечении плоскостями x=h
и y=h
получаем гиперболы ![]() ,
,
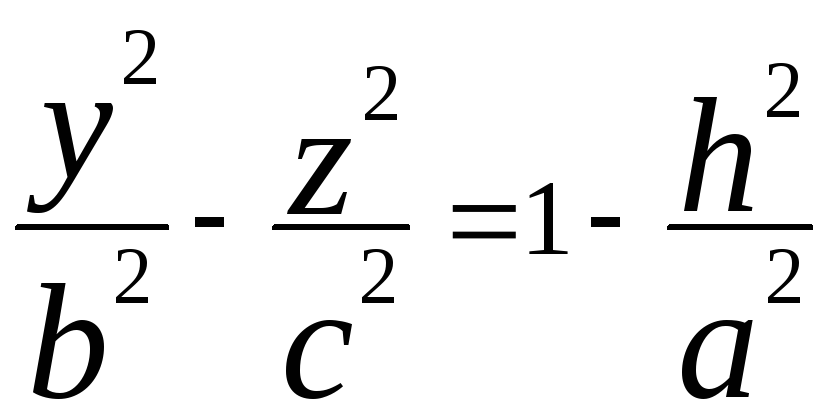 или
или  (4)
(4) 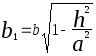 ,
, .В частности при
.В частности при
![]() уравнение (4) имеет вид
уравнение (4) имеет вид 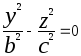 или
или ![]() и
и ![]() - уравнения прямых. Значит, на однополостном
гиперболоиде лежат прямые линии.
- уравнения прямых. Значит, на однополостном
гиперболоиде лежат прямые линии.
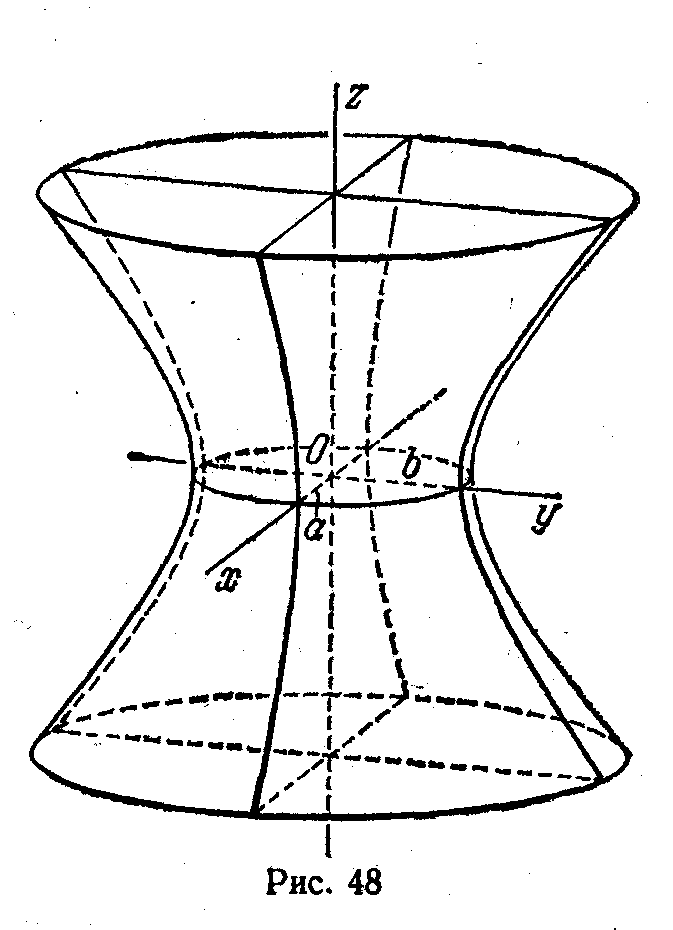
§7. Двухполостный гиперболоид.
Если
вращать гиперболу  вокруг оси OZ,
то в результате получим двухполостный
гиперболоид вращения.
вокруг оси OZ,
то в результате получим двухполостный
гиперболоид вращения.
 (1)
Если растянуть его по оси ОХ в к раз, то
получим общий вид двухполостного
гиперболоида.
Его каноническое уравнение
(1)
Если растянуть его по оси ОХ в к раз, то
получим общий вид двухполостного
гиперболоида.
Его каноническое уравнение  (2), где а=kb.
Если пересекать двухполостный гиперболоид
плоскостями z=h
(h>c),
в сечении получим эллипсы
(2), где а=kb.
Если пересекать двухполостный гиперболоид
плоскостями z=h
(h>c),
в сечении получим эллипсы  или
или  , где
, где  ,
,
 .
При бесконечном возрастании h
.
При бесконечном возрастании h
![]() и
и
![]() , эллипсы увеличиваются ; при h=c
, эллипсы увеличиваются ; при h=c
![]() и
и ![]() =0, эллипсы стягиваются
в точку; при
=0, эллипсы стягиваются
в точку; при
![]() <c.
<c.
![]() и
и ![]() имют мнимые
значения, пересечений нет.
имют мнимые
значения, пересечений нет.
Если
пересекать плоскостями x=h
или y=h
получим в сечении гиперболы
 или
или 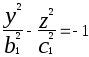

Из сказанного ясно, что двухполостный гиперболоид состоит из двух бесконечных кусков - полостей, отстоящих одна от другой на 2с. Двухполостный гиперболоид имеет три плоскости симметрии - координатные плоскости.
