5. Поверхности второго порядка

§1. Порядок поверхности.

В пространстве аналитическая геометрия изучает поверхности, которые в прямоугольных декартовых координатах определяются алгебраическими уравнениями первой, второй и т.д. степени относительно X,Y,Z:

Ax+By+Cz+D=0 (1)

Аx²+By²+Cz²+2Dxy+2Exz+2Fyz+2Mx+2Ny+2Lz+K=0 (2)

и т.п. Порядок уравнения называется порядком поверхности им определяемой. Мы уже видели, что уравнение первого порядка (линейное) (1) всегда задаёт плоскость - это единственная поверхность первого порядка. Поверхностей второго порядка уже много. Рассмотрим наиболее важные из них.

§2. Цилиндрические поверхности с образующими, параллельными одной из координатных осей.

Пусть в плоскости XОY, например, задана некоторая линия L, её уравнение есть F(x,y)=0 (1) . Тогда множество прямых, параллельных оси oz (образующие) и проходящих через точки на L, образуют поверхность S, называемую цилиндрической поверхностью.

Покажем, что уравнение (1), не содержащее переменной z, и есть уравнение этой цилиндрической поверхности S. Возьмём произвольную точку М(x,y,z), принадлежащую S. Пусть образующая, проходя через М пересекает L в точке N. Точка N имеет координаты N(x,y,0), они удовлетворяют уравнению (1), т.к. (·)N принадлежит L. Но тогда и координаты (x,y,z,) удовлетворяют (1), т.к. оно не содержит z. Значит, координаты любой точки цилиндрической поверхности S удовлетворяют уравнению (1). Значит, F(x,y)=0 - уравнение этой цилиндрической поверхности. Кривая L называется направляющей (кривой) цилиндрической поверхности. Заметим, что в пространственной системе L должна задаваться, вообще-то, двумя уравнениями F(x,y)=0 , z=0, как линия пересечения.

Примеры:

1. Если направляющей служит окружность x²+y²=R², то соответствующая поверхность называется круговым цилиндром.

2. Уравнения,,задают в пространстве соответственно эллиптический цилиндр, параболический цилиндр, гиперболический цилиндр.

Направляющими в плоскости хоу являются эллипс, парабола, гипербола. Очевидно, уравнения F=(y,z)=0 и F(x,z)=0 задают соответственно цилиндрические поверхности с образующими параллельными оси OX и OY. Их направляющие лежат в плоскостях YOZ и XOZ соответственно.

Замечание. Цилиндрическая поверхность не обязательно является поверхностью второго порядка. Например, есть цилиндрическая поверхность 3го порядка, а уравнениеy=sin(x) задаёт синусоидальный цилиндр, которому никакого порядка не приписывают, это вообще, не алгебраическая поверхность.

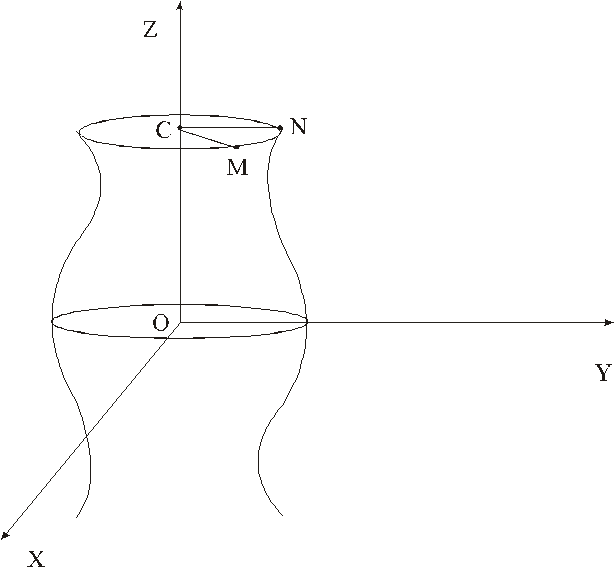
§3. Уравнение поверхности вращения.

Некоторые поверхности 2го порядка являются поверхностями вращения. Пусть в плоскости YOZ лежит некоторая кривая L F(y,z)=0(1). Выясним, каково будет уравнение поверхности S, образованной вращением кривой (1) вокруг оси oz.

Возьмем на поверхности S произвольную точку M(x,y,z). Ее можно считать полученной из (.) N принадлежащей L , тогда аппликаты точек M и N равны (=z). Ордината точки N является тут радиусом вращения, потому .Но С(0,0,z) и потому . Но точка N лежит на кривой и поэтому её координаты ей удовлетворяют. Значит (2) . Уравнению (2) удовлетворяют координаты поверхности вращения S. Значит (2) и есть уравнение поверхности вращения. Знаки «+» или «-» берутся в зависимости от того в какой части плоскости YOZ размещается кривая (1), где у>0 или .

Итак, правило: Чтобы найти уравнение поверхности, образованной вращением кривой L вокруг оси OZ, нужно в уравнении кривой заменить переменную у

на

Аналогично составляются уравнения поверхностей вращения вокруг оси OX и OY.