§8. Собственные числа и собственные векторы в случае симметрической матрицы

Пусть – матрица преобразования и пусть она симметрическая, т.е., тогда.

Из уравнения (3') имеем

.

Так как у нас , то

Так как ,,одновременно, то отсюда следует:

1. подкоренное выражение , т.е. симметрическая матрица имеет всегда вещественные собственные числаи.

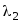2. Эти вещественные собственные числа различны, т.е. . Если бы, тои матрица, имели бы, т.е. имели бы преобразование подобия, что совсем необязательно (у нас произвольное линейное преобразование).

Теорема. Инвариантные направления симметричной матрицы взаимно перпендикулярны.

Доказательство.

Как уже отмечали – первое инвариантное направление,– второе инвариантное направление.

Из уравнения (3') по теореме Виета и учитывая, что , получаем,.

Тогда ,,-ть направлений.

Примем инвариантные направления симметрической матрицы преобразования за новые оси координат, обозначив их и.соответствует собственному числу,соответствует собственному числу.

В старой системе координат ,,.

В новой системе ,,.

(1)

Найдем матрицу преобразования в новой системе координат.

Возьмем вектор , лежащий на оси. Он лежит на инвариантном направлении, соответствующем числу. Поэтому он перейдет в вектор.

Получаем

.

Подставляем в (1), получим ,.

Возьмем вектор , лежащий на другом инвариантном направлении. Он перейдет в вектор.

Подставляя в (1), получим ,.

Окончательно (1) перепишется в виде (2).

Вывод: Если инвариантные направления симметрической матрицы линейного преобразования принять за оси координат, то эта матрица приобретает диагональный вид.

§9. Приведение квадратичной формы к каноническому виду

Рассмотрим квадратичную форму от двух переменных и, т.е. однородный многочлен второй степени относительнои:. Ее можно записать в виде.

Рассмотрим линейное преобразование , где,, причем, матрица этого преобразованиясимметрическая. Тогда имеем. Квадратичная форма перепишется, т.е.– скалярное произведение. Как мы видели, уравнение собственных чиселдля симметрической матрицы имеет два различных действительных корня, и им соответствуют два различных инвариантных направления линейного преобразования:,– угол наклона к осипервого инвариантного направления, и,– второго инвариантного направления. Они перпендикулярны.

Возьмем эти инвариантные направления за новые оси координат и, но так, чтобы система получилась правой, т.е. кратчайший поворот от положительного направления осикбыл против часовой стрелки.соответствует собственному числу,соответствует собственному числу. В новых координатах,. Но. Как установлено выше, матрица преобразования в новых координатах имеет диагональный вид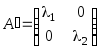, поэтому, и потому– этотвид квадратичной формы и называется каноническим, квадратичная форма содержит лишь квадраты текущих координат и не содержит их произведения.

§10. Приведение общего уравнения второго порядка к каноническому виду

Общее уравнение второго порядка имеет вид

С помощью преобразования поворота

на угол и параллельного переносаобщее уравнение может быть преобразовано к одному из следующих основных видов:

1. –эллипс;

2. –гипербола;

3. или – парабола;

4. –две пересекающиеся прямые;

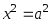5. или – две параллельные прямые.

Если координатные оси новой системы инаправить по двум инвариантным направлениям (повернуть систему на угол), соответствующим собственным числамиматрицы, то квадратичная форма из трех старших членовпримет канонический вид. Группа членов первой степени преобразуется в подобную же группу

Свободный член не изменится.

Полученное уравнение упрощаем далее, производя параллельный перенос осей, в результате чего исчезают члены с первыми степенями координат. Получаем уравнение вида, которое и называетсяканоническим видом уравнения второго порядка. На сколько нужно параллельно переносить оси решается в каждом примере особо (хотя есть и общая теория).

Пример.

Привести к каноническому виду уравнение .

Решение.

. Уравнение собственных чисел ,

, .

Возьмем за первое инвариантное направление то, тангенс которого положителен, т.е. которое образует с осью острый угол. В данном случае. Направление составляет с осьюугол, его берем за ось. Второе направление берем затак, чтобы оно было перпендикулярно первому и составляло правую систему с. Тогда.

, – острый угол,,.

Система повернута на угол, поэтому формулы преобразования будут

(*)

Поворот системы oxy на ,равносилен повороту радиуса-вектора на угол(-),поэтому

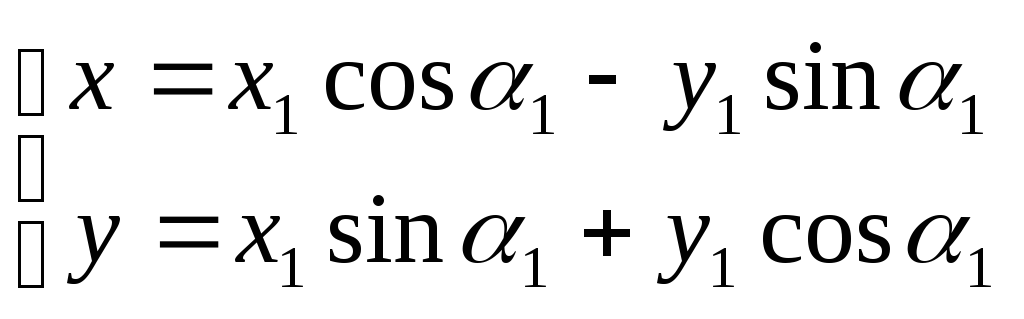
Остальные члены данного уравнения преобразуются:

.

Исходное уравнение в системе запишется:

.

Выделим в нем полные квадраты по и:

или

.

Совершим теперь параллельный перенос системы по формулам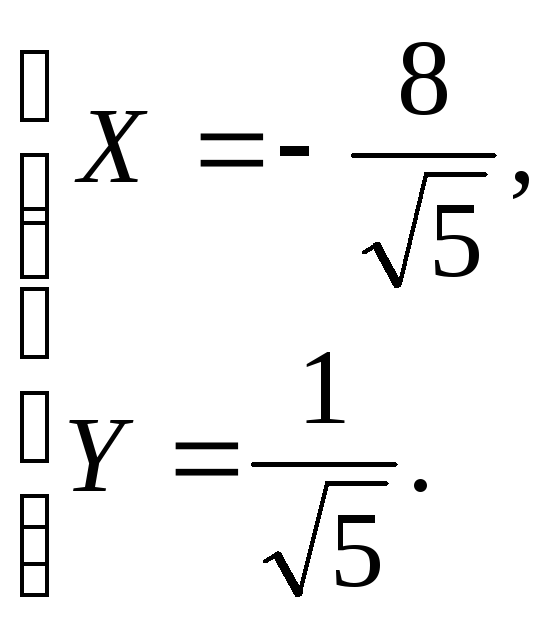Найдем координаты нового начала:,в последний системе координат. В системекоординаты нового началабудут, очевидно:

Используя формулы (*), получаем:

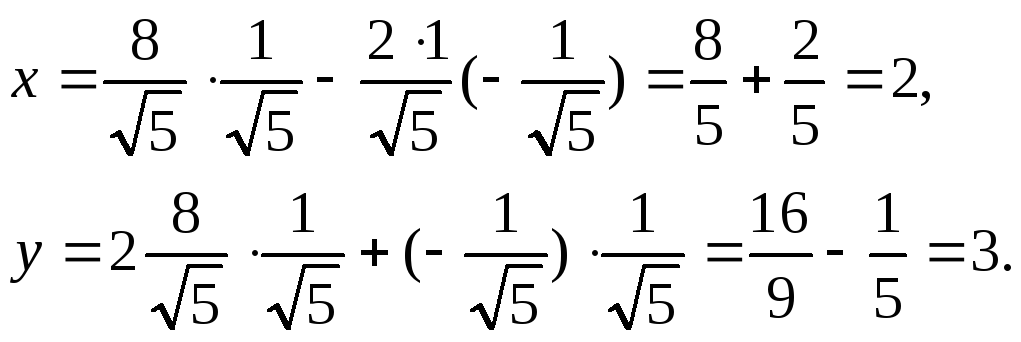
Итак, новое начало в исходной системе будет:.

Уравнение данной кривой в последней системе координат будет иметь вид:или.

Это эллипс с полуосями ,.

Построим чертеж:

1. Строим систему .

2. Строим первое инвариантное направление под углом () и берем его за ось. Ось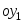строим перпендикулярно и направляем так, чтобы системабыла правой.

3. Наносим на чертеж точку .

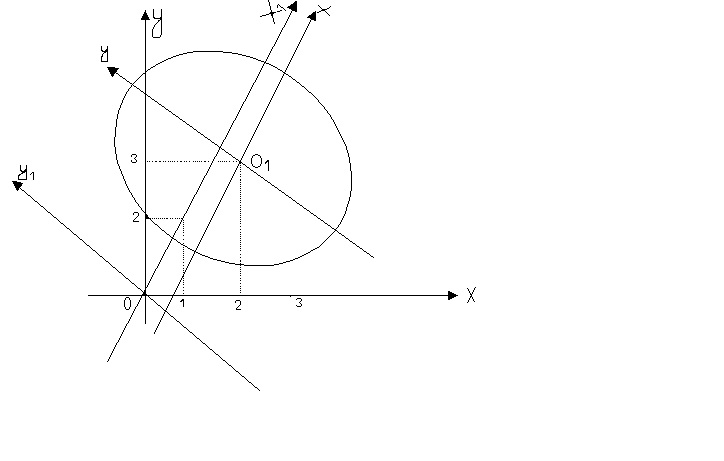4. Переносим в точку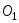начало системы, сохраняя параллельность (направление) осей, получим систему.

5. Строим в этой системе эллипс.