§3. Понятие об обратной матрице

Определение 1. Обратной матрицей по отношению к данной называется матрица, которая будучи умноженной справа (или слева) на данную матрицу, дает единичную матрицу.

Матрицу, обратную к матрице , обозначают. По определению.

Определение 2. Матрица называется неособенной, если: 1) она квадратная; 2) ее определитель отличен от нуля.

Справедлива теорема. Всякая неособенная матрица имеет обратную матрицу (без доказательства).

Практически, если дана неособенная матрица

, т.е. , то,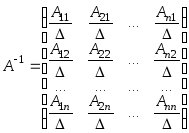

где есть алгебраические дополнения (миноры со знаками) соответствующих элементов. Следует заметить, что при составлении матрицыалгебраические дополнения для элементов-ой строки матрицызаписываются в-ом столбце матрицы(транспонируются).

Пример.

Для матрицы найти обратную.

Определитель , т.е.неособенная..

Оказываются справедливы свойства:

1. Определитель обратной матрицы равен обратной величине определителя исходной матрицы.

2. Обратная матрица произведения равна произведению обратных матриц сомножителей, взятому в обратном порядке.

§4. Решение систем линейных уравнений с помощью обратной матрицы

Пусть дана система линейных уравнений снеизвестными.

(1)

Обозначим матрицу из коэффициентов, черезматрицу-столбец свободных членов, черезматрицу-столбец из неизвестных. Тогда система (1) кратко может быть записана в виде матричного уравнения. (2)

Пусть матрица неособенная, т.е.. Тогда существует обратная матрица.

Умножим обе части уравнения (2) слева на матрицу , получим

или (3),

что и дает решение системы (1).

Пример.

Решить систему уравнений:

Решение.

Запишем систему в матричной форме.

Определитель

Вычислим обратную матрицу :, отсюда.

Значит: ,,.

Замечание. Нетрудно видеть, что матричная формула (3) может быть записана в виде формул,, ...,– Формулы Крамера. Здесьполучается иззаменойk-го столбца столбцом свободных членов .

§5. Решение систем линейных уравнений методом исключения неизвестных (метод Гаусса)

Решение систем линейных уравнений методом обратной матрицы или по формулам Крамера удобно при наличии небольшого числа уравнений, и когда число уравнений и неизвестных совпадает. Если же их много, или количества не совпадают, нужно считать много определителей, что трудоемко. Удобнее оказывается метод последовательного исключения неизвестных.

Пусть дана произвольная система линейных уравнений снеизвестными:

(1)

Матрица ,

составленная из коэффициентов при неизвестных, называется матрицей системы (1).

Матрица ,

получающаяся из добавлением столбца свободных членов, называетсярасширенной матрицей системы (1).

Матрица , очевидно, вполне определяет систему (1).

Определение 1. Под элементарными преобразованиями системы линейных уравнений понимаются следующие операции:

1. умножение какого-либо уравнения системы на число неравное нулю;

2. прибавление к одному уравнению другого уравнения, умноженного на произвольное число;

3. перемена местами двух уравнений в системе.

Делая элементарное преобразование в системе, получаем новую систему. При этом каждому преобразованию системы соответствует такое же преобразование над строчками расширенной матрицы и, очевидно, наоборот.

Решением системы (1) называется любая совокупность значений неизвестных , которая удовлетворяет каждому уравнению системы.

Определение 2. Две системы линейных уравнений от одних и тех же неизвестных называются равносильными (эквивалентными),если каждое решение одной из них является решением другой и наоборот.

Если знаем решения одной из равносильных систем, то мы знаем решение и другой. Поэтому решают ту, что проще. Основой практического решения систем является теорема.

Теорема. При элементарных преобразованиях система переходит в равносильную систему.

При помощи элементарных преобразований можно значительно упростить заданную систему. Решив упрощенную, мы, согласно теореме, найдем решения исходной. Упрощения добиваются разными способами. Наиболее распространен метод Гаусса. При помощи элементарных преобразований систему сводят к такому виду, чтобы ее матрица коэффициентов оказалась трапециевидной или близкой к таковой. Иногда для этого приходится менять нумерацию неизвестных, т.е. в матрице переставлять столбцы. Когда же матрица системы стала трапециевидной, уже нетрудно решить вопрос о совместности системы, о числе решений и найти сами решения. Так как каждому элементарному преобразованию системы соответствует элементарное преобразование над строчками расширенной матрицы этой системы и наоборот, то можно вместо самой системы оперировать с расширенной матрицей системы.

Пример.

Решить систему

Составим расширенную матрицу и элементарными преобразованиями над строчками упростим ее.

Из 3-ей строчки вычтем 4-ую и изменим знак на противоположный.

Заданная система равносильна, таким образом, системе

Отсюда уже легко найдем

, ,,.

Используя матрицы исистемы, нетрудно дать условие совместности системы, т.е. того случая, когда система имеет решение.

Теорема Кронекера-Копелли. Для того, чтобы система линейных уравнений имела решение (была совместна), необходимо и достаточно, чтобы ранг матрицы этой системы был равен рангу ее расширенной матрицы, т.е. чтобы .

О количестве решений при этом говорит другая теорема.

Теорема (о числе решений). Пусть система линейных уравнений совместна, тогда, если ранг матрицы системы равен числу неизвестных (), то система имеет единственное решение, если ранг матрицы системы меньше числа неизвестных (), то система имеет бесконечно много решений, а именно: некоторымнеизвестным можно придать произвольные значения, тогда оставшиесянеизвестных определяются уже единственным образом.