4. Матрицы и их применение

§1. Основные определения. Действия над матрицами

Определение 1. Система чисел, расположенных в прямоугольной таблице изстрок истолбцов,

, (1)

называется матрицей. Строки и столбцы называются рядами матрицы.

Числа , составляющие матрицу, называются ееэлементами. Здесь первый индекс означает номер строки элемента, а второй– номер его столбца.

Для матрицы (1) употребляют и сокращенную запись (;) или. При этом говорят, что матрицаимеет тип.

Если , то матрица называетсяквадратной порядка , если же, то матрица называетсяпрямоугольной. Определитель

называется определителем квадратной матрицы . В частности, матрица может состоять из одного числа, это матрица типа 11: , может состоять из одной строки или одного столбца:

и .

Их типы исоответственно. Квадратная матрица вида

называется диагональной и обозначается кратко . Если всев диагональной матрице, то она называетсяединичной и обозначается буквой . Итак,.

Квадратная матрица называется симметрической, если элементы матрицы, симметрично расположенные относительно главной диагонали, равны между собой. Матрица, все элементы которой равны 0, называется нулевой матрицей и обозначается буквой . Если нужно подчеркнуть тип, то пишут.

Рассмотрим действия над матрицами.

Определение 2. Матрицы исчитаютсяравными, если они одного типа, и соответствующие элементы их равны, т.е. .

Определение 3. Суммой (разностью) матриц иодинакового типа называется матрицатого же типа, элементы которой равны суммам (разностям) соответствующих элементов матрици, т.е..

Пример.

Очевидно выполнение свойств:

1. ,

2. ,

3. .

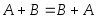Определение 4. Произведение матрицы на число(или, все равно, числана матрицу) называется матрица, т.е. все элементы которой получены из соответствующих элементов умножением на число.

Пример.

Из определения очевидны свойства:

1. ,

2. ,

3. ,

4. ,

5. .

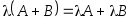Определим умножение двух матриц. Пусть даны матрицы и. Причем, пусть число столбцов матрицыравно числу строк матрицы, т.е..

и

Определение 5. Произведением матриц иназывается матрица

типа , каждый элемент которой получается как сумма произведений элементов-ой строки матрицына соответствующие элементы-ого столбца матрицы:.

Из определения следует, что квадратные матрицы можно перемножать лишь одного порядка.

Пример.

, ,

.

Справедливы свойства:

1. ,

2. ,

3. ,

4. .

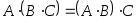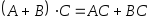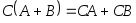Произведение двух матриц не обладает переместительным свойством, т.е. .

Пример.

, .

, ..

Более того, может быть, что произведение существует, ане имеет даже смысла.

Пример.

, ..

не существует, так как число столбцов в больше числа строк в.

Если , то матрицыиназываютсяперестановочными или коммутативными. Например, единичная матрица перестановочна с любой квадратной матрицей того же порядка., т.е.играет роль единицы при умножении.

§2. Понятие ранга матрицы

Пусть дана прямоугольная матрица

.

Если в ней выбрать произвольно столбцов истрок (), то элементы, стоящие на пересечении этих строк и столбцов, образуют квадратную матрицу порядка. Определитель этой матрицы называетсяминором k-го порядка матрицы .

Определение 1. Рангом матрицы называется максимальный порядок минора матрицы, отличного от нуля, т.е.имеет ранг, если

1. найдется хоть один минор в порядка, отличный от нуля;

2. все миноры порядка и выше равны 0. Символически обозначают. Минор порядканазываетсябазисным минором матрицы. Матрица может иметь и несколько базисных миноров, но они все имеют одинаковый порядок .

Практически вычисляют миноры с первого порядка и выше по порядку. Если найден минор r-ого порядка неравный нулю, то оказывается достаточно вычислить лишь миноры порядка, содержащие его. Если они равны нулю все, то ранг матрицы равен. Если хоть один не равен нулю, то операцию применяют к нему.

Пример.

Есть миноры 1-ого и 2-ого порядков неравные нулю. А все третьего – равны нулю, так как содержат строку из нулей. Значит, .

Однако прямое вычисление миноров матрицы очень трудоемко. Поэтому матрицу предварительно преобразуют.

Определение 2. Под элементарным преобразованием матрицы понимают следующие операции:

1. умножение какой-либо строки (столбца) матрицы на число неравное нулю;

2. прибавление к элементам какой-либо строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на одно и то же число;

3. перестановка двух строк (двух столбцов) матрицы.

Справедлива теорема. При элементарном преобразовании ранг матрицы не меняется.

Эту теорему используют для практического вычисления ранга матрицы. Стараются сначала преобразовать матрицу так, чтобы в ней было побольше нулей, а затем уже определяют ранг.

Довольно часто при этом матрица приводится к виду

.

Эта матрица называется трапециевидной.

Например.

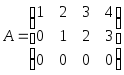
Есть трапециевидная. Как видим, ее ранг легко вычисляется .

Треугольная матрица

–частный случай трапециевидной. тоже трапециевидная.

Оказывается любую матрицу при помощи элементарных преобразований над строчками и перестановок столбцов можно сделать трапециевидной.

Пример.

, .