§ 3. Основные свойства определённого интеграла.
Из определения определённого интеграла (см. (7) § 2) вытекает следующие свойства.
Свойство 1. Если функция f(x) интегрируема на [a,b] и k некоторая постоянная, то функция k f(x) тоже интегрируема на [a,b]
и
(8)
/ постоянный множитель можно выносить за знак определённого интеграла /.
Свойство 2. Если функции f(x) и g(x) интегрируемы на [a,b], то и функция f(x) g(x) тоже интегрируема на
[a,b] и (9)
/ определённый интеграл от алгебраической суммы интегрируемых функций равен алгебраической сумме интегралов от этих функций /.
Доказательство свойств 1 и 2 аналогичны. Докажем второе (первое доказать самостоятельно).
Для любого разбиения [a,b] на элементарные будем иметь
Очевидно, свойство 2 распространяется на любое конечное число слагаемых.
Свойство 3. Если две функции f(x) и g(x) интегрируемы на [a,b] и удовлетворяют на нём условию f(x) g(x), то
(10)
/ неравенство можно почленно интегрировать /.
Доказательство. Рассмотрим разность
Т
.к.
то и вся сумма и её предел (определённый
интеграл) будут неотрицательны,
т.е. или откуда и следует неравенство (10).
Свойство 4. Если функция f(x) интегрируема на [a,b] и удовлетворяет на нём неравенствам m f(x) M (m и M
есть некоторые константы), то (11)
Доказательство. Интегрируя почленно данное неравенство, мы и получим неравенство (11), учитывая то, что
З
десь
мы использовали тот факт, что
есть сумма длин элементарных отрезков,
составляющих отрезок
[a,b]. Каким бы не было разбиение, эта сумма всегда равна длине отрезка b – a.
С
войство
5 (теорема
о среднем).
Если функция
f(x)
непрерывна на отрезке [a,b],
то существует на этом отрезке хоть одна
точка с
такая, что (12)
Доказательство. Считаем, для определённости, что a < b. Пусть m и M есть наименьшее и наибольшее значения непрерывной функции f(x) на [a,b].
Т
огда
и на основании свойства 4 можем записать
О
бозначив
имеем m
M.
Непрерывная на [a,b] функция f(x) должна в некоторой точке x = c, a c b, принимать промежуточное значение (m и M тоже являются значениями f(x)): f(c) = .
Тогда откуда и следует (12).
Замечание. Если f(x) непрерывна (и f(x) 0) на [a,b], то теорема о среднем утверждает, что площадь криволинейной трапеции aABb равна площади некоторого «среднего» прямоугольника aA’ B’ b с тем же основанием [a,b] и некоторой «средней» высотой f(c) (рис. 3).
Рис. 3
С
войство
6. Для
трех произвольных чисел a,
b,
c
всегда справедливо равенство
(13)
если все интегралы существуют.
Доказательство на основе определения (§ 2, (7)) провести самостоятельно. Указание: точка с должна являться одной из точек разбиения отрезка на элементарные отрезки.
§4. Определённый интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
Если в определённом интеграле мы зафиксируем нижний предел а, а верхний предел b будем варьировать, то значение интеграла тоже будет меняться. Т.о. интеграл станет функцией своего верхнего предела.
Д
ля
удобства обозначим верхний (переменный)
предел через х, а переменную интегрирования
черезt
(как мы видели величина интеграла не
зависит от того, какой буквой обозначена
переменная интегрирования). Мы получим
Поскольку он является функцией
своего верхнего предела, то мы её будем
обозначать Ф(х).
Итак Ф(х) = (14)
Г
еометрическое
истолкование этой функции довольно
простое. Для
Рис. 4
каждого х Ф(х) численно равна площади криволинейной трапеции с основанием [a, x]. Очевидно, что эта площадь изменяется с изменением х (рис. 4).
Рассмотрим одно особенно важное свойство функции Ф(х).
Теорема 1. Если функция f(t) непрерывна на [a, b], то производная от определённого интеграла с переменным верхним пределом (14) равна значению этой функции в точке дифференцирования:
Доказательство. Пусть х некоторая точка на [a,b] (рис. 4). Дадим аргументу х в этой точке произвольное приращение х (<> 0). Тогда на основании свойства 6 (§ 3) можем записать
С
оответствующее
приращение функции Ф(х) будет
Применим к последнему интегралу теорему о среднем (свойство 5, § 3)
где ξ
некоторая точка между x
и x+Δx.
Составим отношение приращения функции к приращению аргумента.
Следовательно
/ Здесь мы учли, что при Δx→ 0 х+Δх→ х и, следовательно, ξ→ х тоже, но f(t) непрерывная функция, поэтому f(ξ) → f(x) /.
Замечание. Из доказанной теоремы сразу следует утверждение:
Всякая непрерывная функция имеет первообразную или неопределённый интеграл от непрерывной функции всегда существует.
В
самом деле, для функции f(t),
непрерывной на [a,x],
существует интеграл
т.е. существует функция для которой
Ф’(x)=f(x).
Теорема 2. Если непрерывная на [a,b] функция f(x) имеет на этом отрезке какую-либо первообразную F(x), то
(15)
/ формула (15) называется формулой Ньютона - Лейбница /.
Доказательство.
По условию F(x)
какая-то первообразная функции f(x)
на [a,b].
Но по доказанному функция
тоже первообразная для f(x)
на этом же промежутке могут отличаться
только на постоянную
или
Положим
x
= a
в этом равенстве. Тогда
Итак:
C=
-F(a)
и потому
Положим
x
= b
в этом равенстве, мы получим
Заменяя здесь t на x, что для интеграла все равно, мы и получим формулу (15).
Введём
обозначение:
-
«двойная подстановка от а до b».
Теперь формулу (15) можно переписать в
виде:
(16)
Замечание.
Как мы знаем, неопределённый интеграл
есть первообразная (тоже совокупность
первообразных) для f(x):
.
Но тогда в формуле (16) в качестве
первообразнойF(x)
мы
можем
брать
Тем самым формула Ньютона – Лейбница
приобретает форму особенно удобную и
ш
ироко
используемую на практике:
(17)
Итак, во многих случаях вычисление определённого интеграла сводится к вычислению соответствующего неопределённого интеграла.
Примеры.1)
Самостоятельно вычислить (применяя формулу (17)):
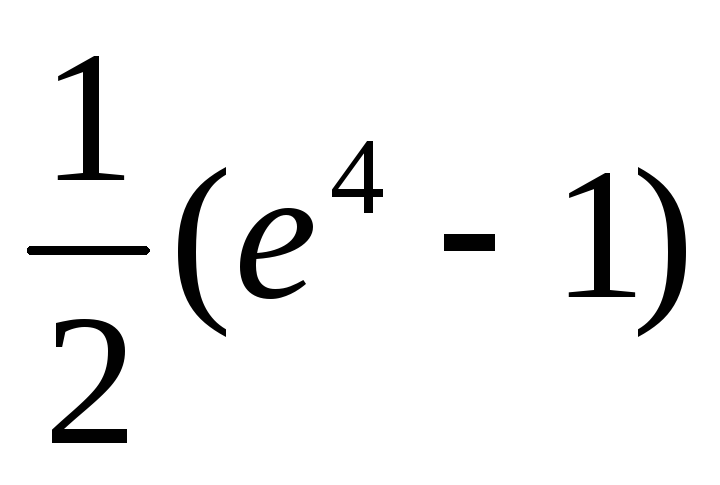
Ответ:
Ответ:
